Bài giảng Toán 10 (Sách Kết nối tri thức với cuộc sống) – Chương VII, Bài 22: Ba đường conic (Phần 3)

Tài liệu này là một chương trong sách giáo khoa Toán Hình học, tập trung vào phương pháp tọa độ trong mặt phẳng. Chương này bao gồm các khái niệm cơ bản về phương trình đường thẳng, đường tròn và ba đường conic (elip, hypebol, parabol), cùng với các ứng dụng thực tế của chúng.

Học sinh, sinh viên học môn Toán Hình học

Chương này trình bày các kiến thức về phương pháp tọa độ trong mặt phẳng, bao gồm:

1. **Phương trình đường thẳng:** Nghiên cứu các dạng phương trình đường thẳng (tổng quát, tham số, chính tắc) và các bài toán liên quan đến vị trí tương đối giữa các đường thẳng.
2. **Đường thẳng trong mặt phẳng tọa độ:** Ứng dụng phương pháp tọa độ để giải các bài toán liên quan đến đường thẳng.
3. **Phương trình đường tròn:** Xây dựng phương trình đường tròn và các bài toán liên quan.
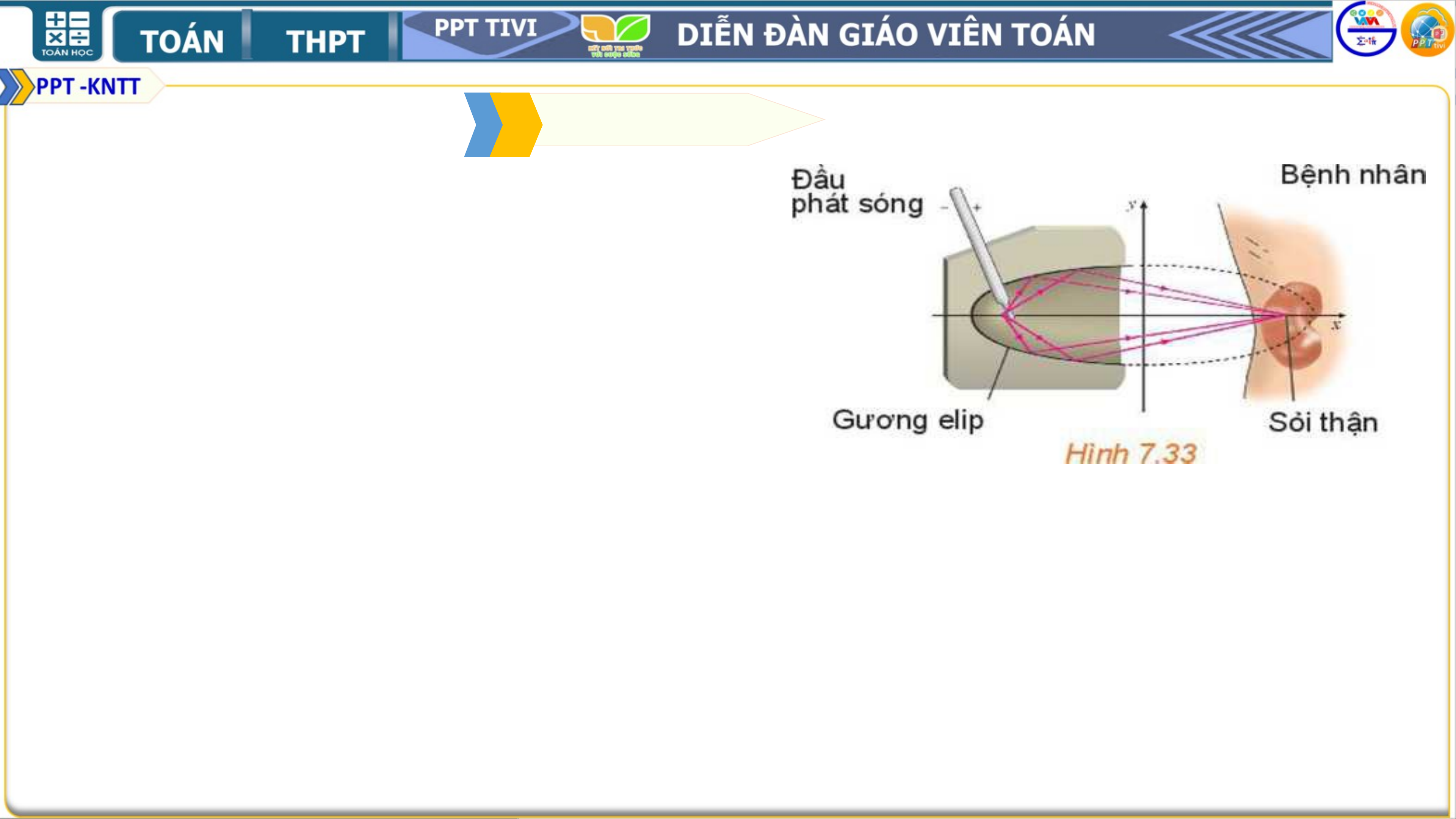
4. **Ba đường conic (elip, hypebol, parabol):** Nghiên cứu định nghĩa, phương trình chính tắc và các tính chất hình học của ba đường conic. Đặc biệt, chương này còn đề cập đến ứng dụng của chúng trong thực tế, ví dụ như quỹ đạo của các hành tinh là hình elip (theo định luật Kepler), hệ thống định vị LORAN sử dụng tính chất của hypebol, và bài toán Apollonius liên quan đến việc tìm đường tròn tiếp xúc với ba đường tròn cho trước, có thể giải bằng cách xác định giao của các đường conic.
5. **Ứng dụng thực tế:** Chương này cũng đề cập đến một số ứng dụng thực tế của các đường conic, chẳng hạn như trong thiên văn học (quỹ đạo elip của các hành tinh) và hệ thống định vị (sử dụng hypebol).