Chương 3:
SUY DIỄN THỐNG KÊ VÀ DỰ BÁO
Nguyễn Phương
Bộ môn Toán kinh tế
Đại học Ngân hàng TPHCM
Email: nguyenphuong0122@gmail.com
Ngày 5 tháng 12 năm 2022
1
NỘI DUNG
1Quy luật phân phối xác suất của một số thống kê mẫu
2Khoảng tin cậy cho hệ số hồi quy
Khoảng tin cậy cho một hệ số hồi quy
Khoảng tin cậy cho biểu thức của hai hệ số hồi quy
3Khoảng tin cậy cho phương sai sai số ngẫu nhiên
4Kiểm định giả thuyết về hệ số hồi quy
Kiểm định giả thuyết về một hệ số hồi quy
Kiểm định giả thuyết về một hệ số hồi quy- Kiểm định T(t-test)
Kiểm định về một ràng buộc giữa các hệ số hồi quy - Kiểm định T (t-test)
Kiểm định về nhiều ràng buộc của các hệ số hồi quy-kiểm định F
Kiểm định sự phù hợp của hàm hồi quy
5Dự báo giá trị của biến phụ thuộc
Dự báo giá trị trung bình
Dự báo giá trị cá biệt
2
Quy luật phân phối xác suất của một số thống kê mẫu
Giả thiết 5: Các sai số ngẫu nhiên có phân phối chuẩn:
ui∼N(0, σ2).
Định lý
Khi các giả thiết 1 - 5 thỏa mãn, ta có:
t=b
βj−βj
se(b
βj)
∼tn−k
3
Khoảng tin cậy cho hệ số hồi quy Khoảng tin cậy cho một hệ số hồi quy
Xét mô hình hồi quy
Y=β1+β2X2+... +βkXk+u
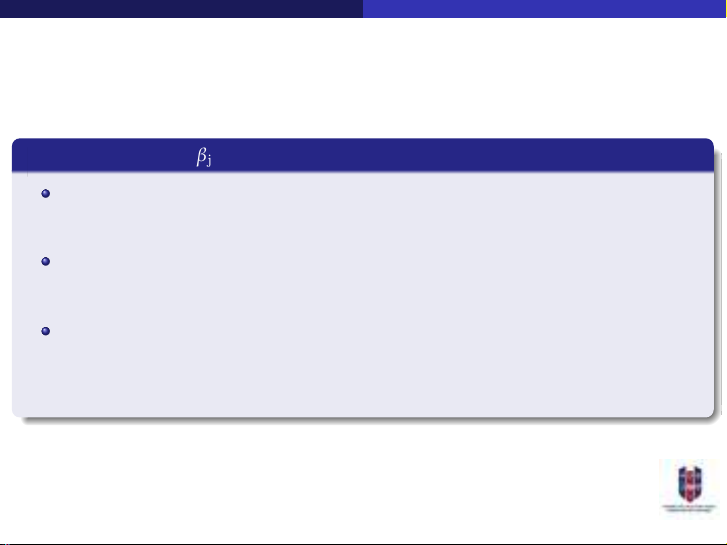
Khoảng tin cậy của βj
Khoảng tin cậy đối xứng
ˆ
βj−tα/2(n−k)se(ˆ
βj); ˆ
βj+tα/2(n−k)se(ˆ
βj);
Khoảng tin cậy bên phải (dùng để ước lượng tối thiểu cho βj)
ˆ
βj−tα(n−k)se(ˆ
βj); +∞;
Khoảng tin cậy bên trái (dùng để ước lượng tối đa cho βj)
−∞;ˆ
βj+tα(n−k)se(ˆ
βj);
trong đó tα(n)là giá trị tới hạn Student bậc n mức α.
Ý nghĩa: Khoảng tin cậy (1−α)∗100%cho hệ số góc βj(j=1,2, ..., k)cho
biết khi biến Xjtăng 1 đơn vị và các biến khác trong mô hình không đổi thì
giá trị trung bình của biến phụ thuộc thay đổi trong khoảng nào.
4
Khoảng tin cậy cho hệ số hồi quy Khoảng tin cậy cho một hệ số hồi quy
Ví dụ
Từ số liệu đã cho của ví dụ trước về chi tiêu và thu nhập. Hãy ước lượng
khoảng tin cậy 95% của β2và nêu ý nghĩa.
Ví dụ
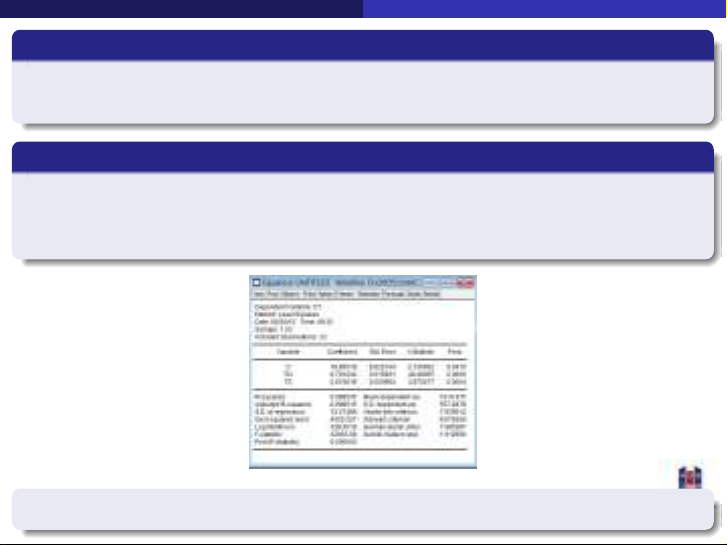
Sử dụng tập số liệu ch2vd5.wf1. Ước lượng hàm hồi quy tuyến tính của CT
(chi tiêu, triệu đồng/năm) theo TN (thu nhập từ lao động, triệu đồng/năm)
và TS (giá trị tài sản, tỷ đồng), ta được:
Hãy ước lượng khoảng tin cậy 95% của β1, β2và β3.
5