ĐỒ THỊ
Nguyễn Quỳnh Diệp
diepnq@tlu.edu.vn
1
CHƯƠNG 5
Nguyễn Quỳnh Diệp
File Bài giảng: goo.gl/Y3cpLF hoặc goo.gl/TYxXQD
NỘI DUNG
•Các định nghĩa
•Các thuật ngữ về đồ thị
•Biểu diễn đồ thị
•Tính liên thông
•Đường đi Euler và đường đi Hamilton
•Bài toán đường đi ngắn nhất
Toán rời rạc 2
Nguyễn Quỳnh Diệp
Toán rời rạc 3
5.1. CÁC ĐỊNH NGHĨA
Nguyễn Quỳnh Diệp
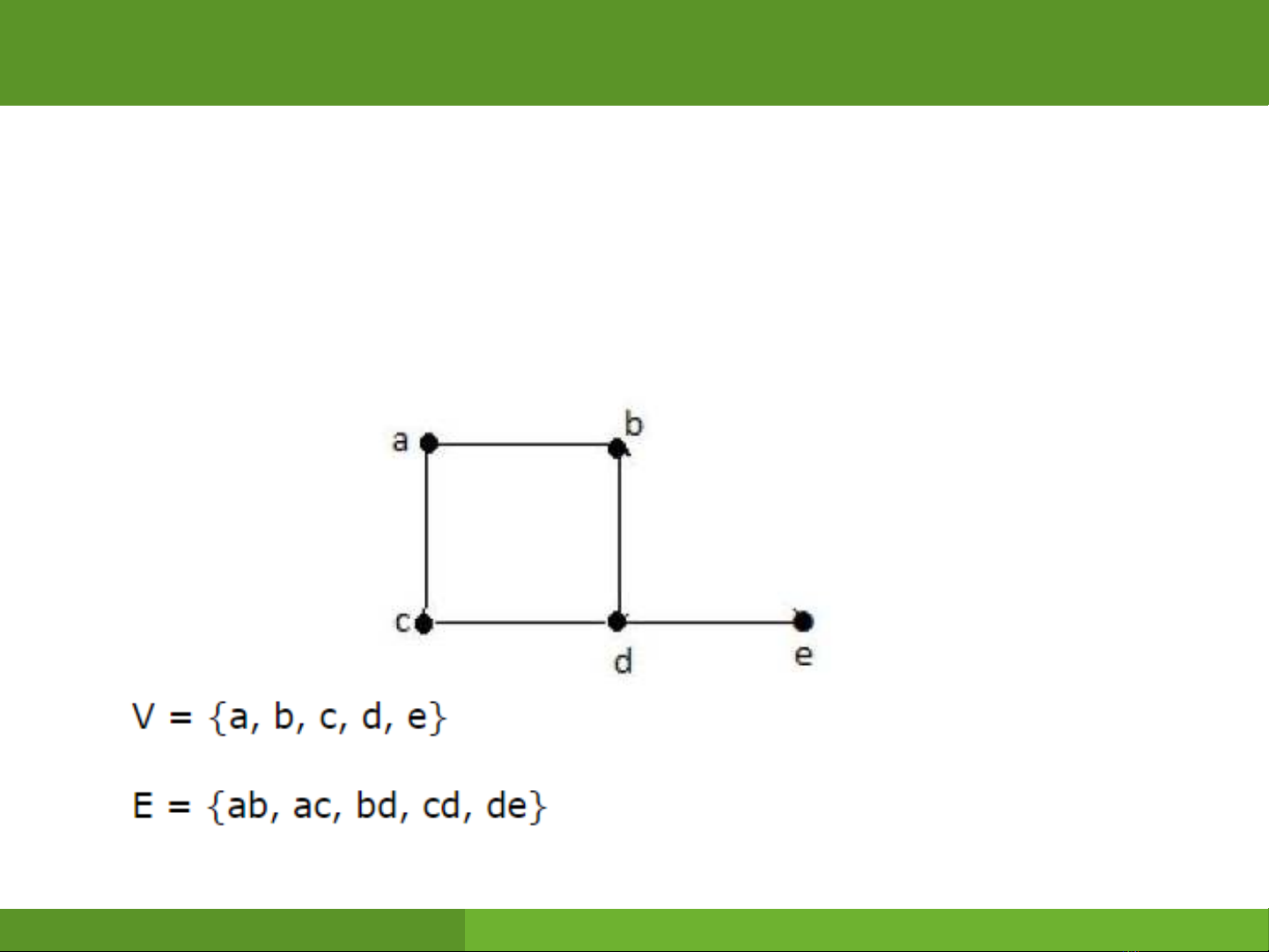
ĐỒ THỊ
Toán rời rạc 4
•Đồ thị là một cấu trúc rời rạc
•Gồm các đỉnh (V) và các cạnh (E) nối đỉnh
Nguyễn Quỳnh Diệp
ĐỒ THỊ
Toán rời rạc 5
•Dùng đồ thị cho các lĩnh vực khác nhau:
Kĩ sư điện: dùng đồ thị để thiết kế các mạch điện
Ngành khoa học: biểu diễn cấu trúc hóa học của các chất, cấu
trúc DNA…
Ngành ngôn ngữ học: biểu diễn cây ngôn ngữ
•Các ứng dụng khác của đồ thị
Biểu diễn sự ảnh hưởng của một ai đó trong tổ chức
Biểu diễn kết quả cuộc thi thể thao
Mạng hàng không
Nguyễn Quỳnh Diệp