1
30 October 2012 1
Toán rời rạc (5):
MỘT SỐ BÀI TOÁN TỐI ƯU
TRÊN ĐỒ THỊ
Ts. Hoàng ThịThanh Hà
Khoa Thống kê –Tin học
Trường Đại học Kinh tế
30 October 2012 2
Nội dung
1. MỘT SỐ BÀI TOÁN TRÊN ĐỒ THỊ
2. THUẬT TOÁN DIJKSTRA
3. THUẬT TOÁN FLOYD TÌM KHOẢNG
CÁCH CỦA CÁC CẶP ĐỈNH
30 October 2012 3
MỘT SỐ BÀI TOÁN TRÊN ĐỒ THỊ
Mở đầu:
Trong đời sống, chúng ta thường gặp những
tình huống nhưsau: để đi từ địađiểm A đếnđịa
điểm B trong thành phố, có nhiềuđường đi,
nhiều cách đi; có lúc ta chọnđường đi ngắn
nhất (theo nghĩa cựly), có lúc lại cần chọn
đường đi nhanh nhất (theo nghĩa thời gian) và
có lúc phải cân nhắcđể chọnđường đi chi phí
thấp nhất, v.v...
30 October 2012 4
MỘT SỐ BÀI TOÁN TRÊN ĐỒ THỊ
Có thểcoi sơ đồ củađường đi từAđến B trong
thành phốlà mộtđồ thị, vớiđỉnh là các giao lộ
(A và B coi nhưgiao lộ), cạnh là đoạnđường
nối hai giao lộ. Trên mỗi cạnh củađồ thịnày, ta
gán một sốdương, ứng với chiều dài củađoạn
đường, thời gian điđoạnđường hoặc cước phí
vận chuyển trên đoạnđường đó, ...
30 October 2012 5
MỘT SỐ BÀI TOÁN TRÊN ĐỒ THỊ
a) ĐN: Đồ thịcó trọng sốlà đồ thịG=(V,E) mà mỗi cạnh
e∈Eđược gán bởi một sốthực m(e), gọi là trọng sốcủa
cạnh (hoặc cung) e
–Ở đây trọng sốcủa mỗi cạnh được xét là một sốdương và còn
gọi là chiều dài của cạnh đó.
–Mỗiđường đi từ đỉnh u đếnđỉnh v, có chiều dài là m(u,v), bằng
tổng chiều dài các cạnh mà nó đi qua. Khoảng cách d(u,v) giữa
hai đỉnh u và v là chiều dài đường đi ngắn nhất trong các đường
đi từuđến v.
Có thểxem mộtđồ thịG bất kỳlà mộtđồ thịcó trọng số
mà mọi cạnh đều có chiều dài 1. Khi đó, khoảng cách
d(u,v) giữa hai đỉnh u và v là chiều dài củađường đi từu
đến v ngắn nhất, tức là đường đi qua ít cạnh nhất.
30 October 2012 6
THUẬT TOÁN DIJKSTRA
Cho đơnđồ thịliên thông, có trọng sốG=(V,E). Tìm
khoảng cách d(u0,v) từmộtđỉnh u0cho trướcđến một
đỉnh v bất kỳcủa G và tìm đường đi ngắn nhất từu0đến v.
Có một sốthuật toán tìm đường đi ngắn nhất; ở đây, ta có
thuật toán do E. Dijkstra, nhà toán học người Hà Lan, đề
xuất năm 1959. Trong phiên bản mà ta sẽtrình bày, người
ta giảsử đồ thịlà vô hướng, các trọng sốlà dương. Chỉ
cần thay đổiđôi chút là có thểgiảiđược bài toán tìm
đường đi ngắn nhất trong đồ thịcó hướng.
2
30 October 2012 7
THUẬT TOÁN DIJKSTRA
b) Phương pháp của thuật toán Dijkstra: xác định tuần
tự đỉnh có khoảng cách đến u0từnhỏ đến lớn.
Trước tiên, đỉnh có khoảng cách đến a nhỏnhất chính là a,
với d(u0,u0)=0. Trong các đỉnh v ≠u0, tìm đỉnh có khoảng
cách k1đến u0là nhỏnhất. Đỉnh này phải là một trong các
đỉnh kềvới u0. Giảsử đó là u1. Ta có: d(u0,u1) = k1.
Trong các đỉnh v ≠u0và v ≠u1, tìm đỉnh có khoảng cách
k2đến u0là nhỏnhất. Đỉnh này phải là một trong các đỉnh
kềvới u0hoặc với u1. Giảsử đó là u2. Ta có: d(u0,u2) = k2.
Tiếp tục nhưtrên, cho đến bao giờtìm được khoảng cách
từu0đến mọiđỉnh v của G. Nếu V={u0, u1, ..., un} thì:

30 October 2012 8
THUẬT TOÁN DIJKSTRA
b). Ma trn khong cách.
Cho G=(V,E) V={v1,v2,…,vn}làđơn đ th
cótrng s.Ma trn khong cách ca G
làma trn D= (dij) xác đnh như sau
d(ij)= {0 nếu i=j
W(vi,vj) khi (vi,vj) ∈E
∞khi ∉E
30 October 2012 9
THUẬT TOÁN DIJKSTRA
c)Thut toánDijkstra
Bưc1. i:=0, S:=V\{u0}, L(u0):=0, L(v):= ∞vi mi v∈S
vàđánh duđnh v bi (∞,-). Nu n=1 thìxut
d(u0,u0)=0 =L(u0)
Bưc2. Vi mi v ∈S vàkvi ui(nuđ thcóhung
thìv làđnh sau ca ui), đt L(v):=min
{L(v),L(ui)+w(ui,v)}, đánh du v bi (L(v);ui) nu L(v)
cósthay đi.
Xácđnh k =min L(v) (v∈S)
Nu k=L(vj) thìxut d(u0,vj)=k vàui+1:=vjS:=S\{ui+1}
Bưc3 i:=i+1
Nu i = n-1 thìkt thúc (hoc S rng) , nu không thì
quay li Bưc 2
30 October 2012 10
THUẬT TOÁN DIJKSTRA
Bài tp 1. Tìm đưng đi ngn nht t u0đn các
đnh còn li
30 October 2012 11
THUẬT TOÁN DIJKSTRA
30 October 2012 12
THUẬT TOÁN DIJKSTRA
3
30 October 2012 13
THUẬT TOÁN FLOYD
Sử dụng ma trận Wn x n để tính độ dài đường đi ngắn
nhất giữa tất cả các cặp đỉnh.
1) Bắt đầu gán W0:= ma trận trọng số M
2) Thực hiện nlần lặp trên W. Sau bước lặp thứ
k, W[i,j] chứa độ dài đường đi ngắn nhất từ đỉnh
i đến đỉnh j mà chỉ đi qua các đỉnh có chỉ số
không vượt quá k:
W(k)[i,j] := min ( W(k-1)[i,j] , W(k-1)[i,k] + W(k-1)[k,j] ) ,
với k= 1, 2, ... , n.
30 October 2012 14
THUẬT TOÁN FLOYD
Dữliệu vào: Ma trận trọng sốM củađồ thị và kết quả: Ma
trận Wn chứa khoảng cách của tất cảcác cặpđỉnh.
BEGIN
for i:= 1 to ndo
for j:= 1 to ndo W[i,j] := M[i,j]
for i := 1 to ndo W[i,i] := 0 {Khoảng cách từ một điểm đến
chính nó = 0}
for k:= 1 to ndo
for i:= 1 to ndo
for j:= 1 to ndo
if W[i,j] > W[i,k] + W[k,j] then
W[i,j] := W[i,k] + W[k,j]
{W[i,j] là phần tử dòng i cột j của ma trận Wk}
END .
30 October 2012 15
THUẬT TOÁN FLOYD
Định lý: Thuật toán Floyd cho ta ma trận W*=Wn
là ma trận khoảng cách nhỏnhất củađồ thịG.
30 October 2012 16
THUẬT TOÁN FLOYD
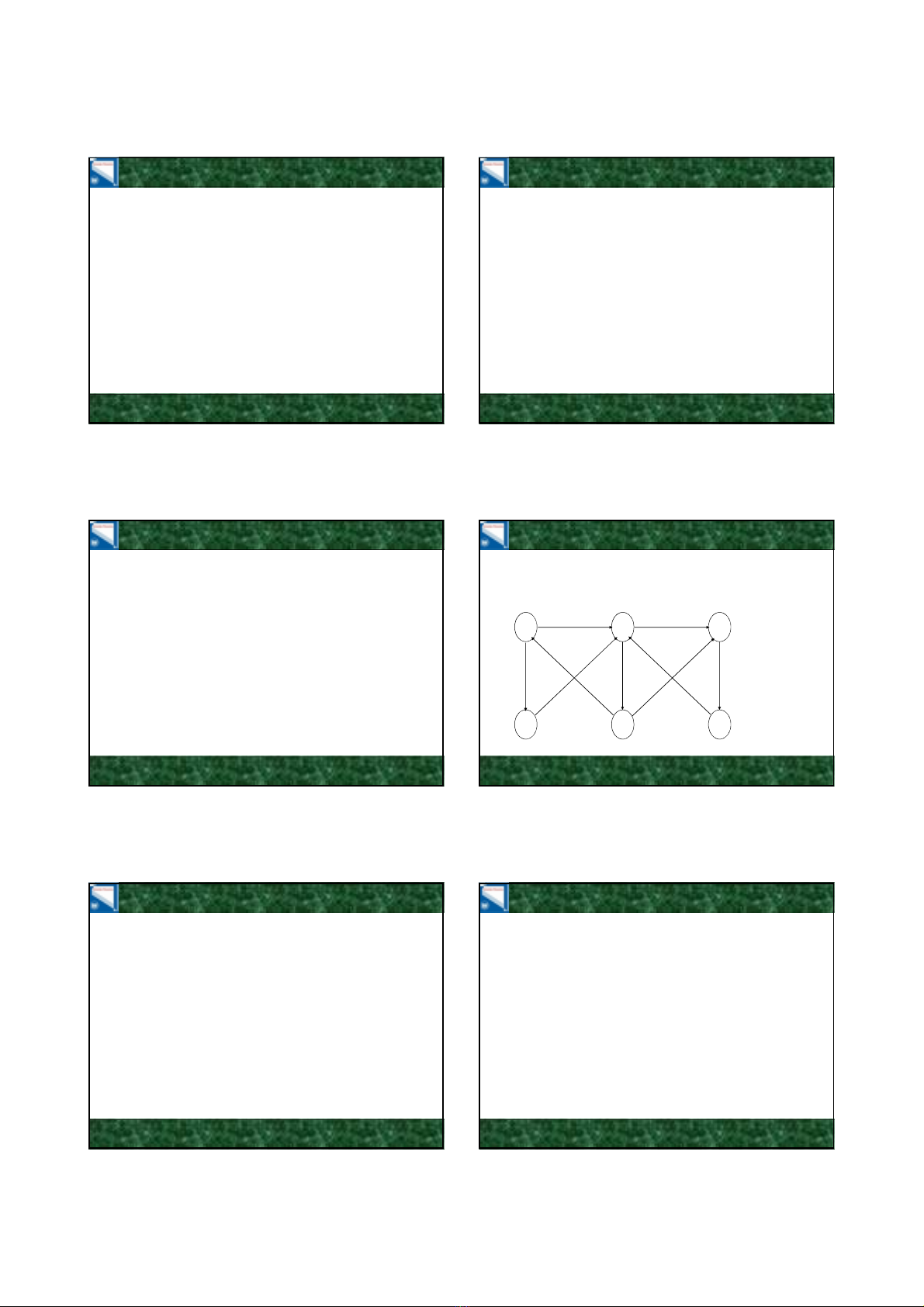
Ví dụ:Xét đồ thịG sau:
v1v2v3
v4v5v6
4
7
22
4
11
2
3
30 October 2012 17
THUẬT TOÁN FLOYD
Áp dụng thuật toán Floyd, ta tìm được (các ô
trống là ∞)

1
22
4
3
14
27
30 October 2012 18
THUẬT TOÁN FLOYD
1
4292
4
3
14
27
251
104292
584
3
14
82117

4
30 October 2012 19
THUẬT TOÁN FLOYD
8251
5104292
11584
3
714
1482117
8251
594282
11584
3
714
1372106

30 October 2012 20
THUẬT TOÁN FLOYD
726414
594282
1059747
3
615393
1272969
726414
574262
1059747
359747
615373
1272969
