
BÀI KI M TRA 1 TI T CH NG IỂ Ế ƯƠ
−−−−−−−−−−−−− (Hình h c ọ− Ch ng trình chu n)ươ ẩ
I. M c đích, yêu c uụ ầ : + Ôn t p, h th ng và đánh giá vi c lĩnh h i ki n th c hình ch ng I.ậ ệ ố ệ ộ ế ứ ươ
+ Hi u rõ khái ni m v hình đa di n, v n d ng công th c đ tính th tích c a kh i đaể ệ ề ệ ậ ụ ứ ể ể ủ ố
di nệ
II. M c tiêuụ:
+ V ki n th c:ề ế ứ − N m đ c khía ni m v hình đa di n và kh i đa di n, kh i đa di n đ u và th tích c aắ ượ ệ ề ệ ố ệ ố ệ ề ể ủ
kh i đa di n.ố ệ
− N m đ c phép d i hình trong không gian.ắ ượ ờ
+ V k năng:ề ỹ − Phân lo i đ c kh i đa di n đ u.ạ ượ ố ệ ề
− Xác đ nh đ c m t ph ng đ i x ng c a kh i t di n đ u.ị ượ ặ ẳ ố ứ ủ ố ứ ệ ề
− Tính đ c th tích c a kh i đa di n và chi u cao c a kh i chóp.ượ ể ủ ố ệ ề ủ ố
III. Ma tr n đậ ề:
M c đứ ộ
N i dungộ
Nh n bi t ậ ế Thông hi uểV n d ngậ ụ
T ngổ
TN TL TN TL TN TL
1. Khái ni mệ
v kh i đa di nề ố ệ 2
0,8
1
0,4
1
1,0
4
2,2
2. Kh i đa di nố ệ
l i và kh i đaố ố
di n đ uệ ề
2
0,8
1
0,4
1(Hv)
1
4
2,2
3. Khái ni mệ
v th tích c aề ể ủ
kh i đa di nố ệ
1
0,4
1
0,4
1
2,5
2
0,8
1
1,5
6
5,6
5
2
6
5,7
3
2,3
14
10
IV. Đ bàiề:
A. TR C NGHI MẮ Ệ : (4 đi m, m i câu 0,4 đi m).ể ỗ ể
Câu 1(NB): Cho kh i l p ph ng ABCD.A’B’C’D’, m t (ACC’A’) c a kh i l p ph ng đó chia kh i đóố ậ ươ ặ ủ ố ậ ươ ố
thành bao nhiêu kh i đa di n:ố ệ
A/ 2; B/ 3; C/ 4; D/ 5.
Câu 2(NB): Ch n kh ng đ nh ọ ẳ ị sai. Trong m t kh i đa di n:ộ ố ệ
A/ Hai m t b t kỳ luôn có ít nh t m t đi m chung;ặ ấ ấ ộ ể B/ M i đ nh là đ nh chung c a ít nh t 3 m t;ỗ ỉ ỉ ủ ấ ặ
C/ M i m t có ít nh t ba c nh;ỗ ặ ấ ạ D/ M i c nh c a m t kh i đa di n cũng là c nh chung c a đúng 2 m t;ỗ ạ ủ ộ ố ệ ạ ủ ặ
Câu 3(TH): Hình t di n đ u có bao nhiêu tâm đ i x ng?ứ ệ ề ố ứ
A/ 1; B/ 2; C/ 3; D/ Không có.
Câu 4(TH): Cho ba m nh đ :ệ ề (I): Kh i đa di n đ u lo i {4; 3} là kh i l p ph ng;ố ệ ề ạ ố ậ ươ
(II): Kh i đa di n đ u lo i {3; 5} là kh i hai m i m t đ u;ố ệ ề ạ ố ươ ặ ề
(III): Kh i đa di n đ u lo i {3; 4} là kh i m i m t đ u.ố ệ ề ạ ố ườ ặ ề
S m nh đ đúng trong 3 m nh đ trên là:ố ệ ề ệ ề
A/ 0; B/ 1; C/ 2; D/ 3.
Câu 5(NB): Trong đ nh nghĩa kh i đa di n đ u lo i {p; q}. Xét ba m nh đ sau:ị ố ệ ề ạ ệ ề
M = “p là s c nh c a m i m t kh i đa di n đ u”ố ạ ủ ỗ ặ ố ệ ề
N = “p là s c nh c a kh i đa di n đ u”ố ạ ủ ố ệ ề
P = “M i đ nh c a kh i đa di n đ u là đ nh chung c a đúng q m t”ỗ ỉ ủ ố ệ ề ỉ ủ ặ
Khi đó ta có:
A/ Ch M đúng;ỉB/ Ch N đúng;ỉC/ N và P đúng; D/ M và P đúng.
Câu 6(NB): Kh i đa di n đ u lo i {4; 3} là:ố ệ ề ạ
A/ Kh i đa di n đ u 4 c nh, 3 m t;ố ệ ề ạ ặ B/ Kh i đa di n đ u có 6 m t, 12 c nh và 8 đ nh;ố ệ ề ặ ạ ỉ
C/ Kh i đa di n có 3 c nh và 4 m t;ố ệ ạ ặ D/ Kh i đa di n có 12 c nh, 12 đ nh và 6 đ ng chéo.ố ệ ạ ỉ ườ

Câu 7(TH): Cho kh i chóp có th tích b ng ố ể ằ
1
6
m3 và di n tích đáy b ng ệ ằ
1
4
m2. Khi đó, chi u cao c a kh iề ủ ố
chóp b ng:ằA/ 1m; B/ 2m; C/ 3m; D/
1
3
m.
H
M
B
D
C
A
C âu 8(NB) : Cho kh i lăng tr có di n tích đáy b ng ố ụ ệ ằ
S
và chi u cao b ng ề ằ
h
. Khi đó, th tích c a kh i lăngể ủ ố
tr b ng:ụ ằ
A/
1.
3S h
; B/
1.
6S h
; C/
1.
2S h
. D/ S.h.
Câu 9(VD): Khi đ dài c nh c a m t kh i l p ph ng tăng lên k l n thì th tích kh i l p ph ng đó tăngộ ạ ủ ộ ố ậ ươ ầ ể ố ậ ươ
lên:
A/ k l n;ầB/ 3k l n;ầC/ k3 l n;ầD/ k2 l n.ầ
Câu 10(VD) Cho kh i chóp S.ABCD có đáy ABCD là hình vuông c nh ố ạ
a
. SA vuông góc v i đáy và SA = ớ
a
.
G i I là trung đi m c a SC. Th tích kh i chóp I.ABCD b ng:ọ ể ủ ể ố ằ
A/
3
6
a
; B/
3
2
4
a
; C/
3
12
a
; D/
3
2
9
a
.
B. T LU NỰ Ậ : (6 đi m)ể
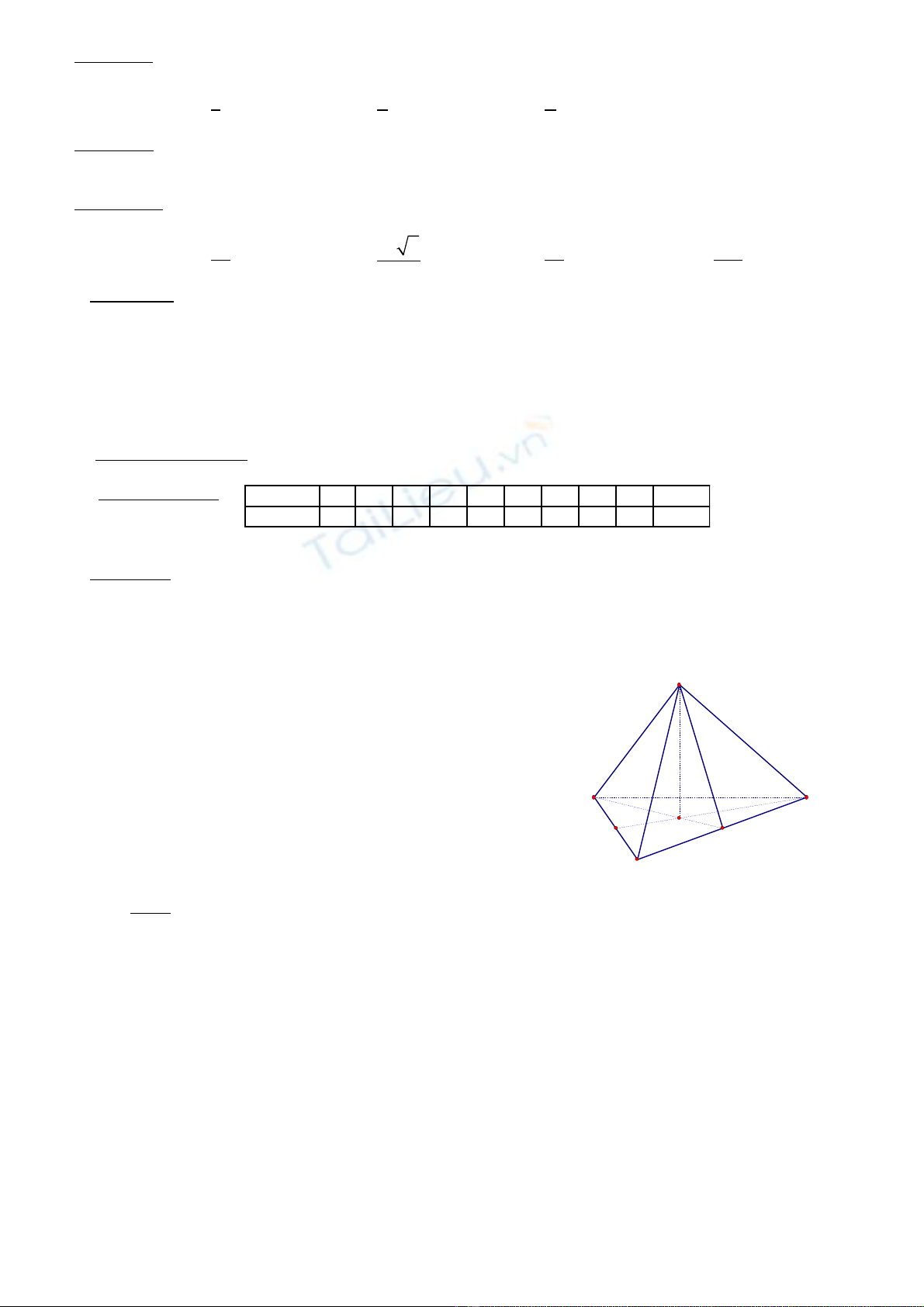
Cho t di n đ u ABCD c nh b ng 2a. G i M là trung đi m c a CD.ứ ệ ề ạ ằ ọ ể ủ
1/ Ch ra m t m t ph ng đ i x ng c a t di n ABCD (Không yêu c u ch ng minh) ỉ ộ ặ ẳ ố ứ ủ ứ ệ ầ ứ
2/ Tính th tích c a kh i t di n ABCD.ể ủ ố ứ ệ
3/ Tính kho ng cách t đi m M đ n mp(ABC).ả ừ ể ế
− − − − − − − − − − − − @ − − − − − − − − − − − −
V. Đáp án và bi u đi m:ể ể
A. TR C NGHI MẮ Ệ :
B. T LU NỰ Ậ :
Hình v (1 đi m) ẽ ể
- T di n: 0,5 đ.ứ ệ
- Ph c v câu b: 0,5 đ.ụ ụ
1/ 1 đi m.ể
+ Ch ra đ c m t ph ng (ABM) (ho c m t m t khác) ỉ ượ ặ ẳ ặ ộ ặ 1,0 đi m.ể
2/ 2,5 đi m.ể
+ Ghi đúng công th c th tíchứ ể 0,5 đi mể
+ Xác đ nh và tính đ c chi u cao c a kh i t di nị ượ ề ủ ố ứ ệ 1,0 đi mể
+ Tính đúng di n tích đáyệ0,5 đi mể
+ Tính đúng th tíchể0,5 đi m.ể
3/ 1,5 đi mể
+ Tính đúng th tích kh i t di n ABCMể ố ứ ệ 0,5 đi mể
+ Áp d ng công th c th tích c a t di n ABCM đ ụ ứ ể ủ ứ ệ ể
suy ra kho ng cách t M đ n mp(ABC)ả ừ ế 0,25 đi m.ể
+ Tính đúng k t qu kho ng cáchế ả ả 0,25 đi mể
Chú ý: N u h c sinh gi i cách khác thì giáo viên căn c vào bài làm c a h c sinh mà cho đi m cho t ngế ọ ả ứ ủ ọ ể ừ
câu đúng v i bi u đi m trên.ớ ể ể ở
Câu 12345678910
Đáp án A A D C D B B D C A


























