ĐỀ KIỂM TRA GIỮA HỌC KỲ I NĂM HỌC ……
MÔN: TOÁN 12 – ĐỀ 1
Thời gian làm bài: 90 phút
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Mỗi câu hỏi thí sinh chỉ chọn một
phương án.
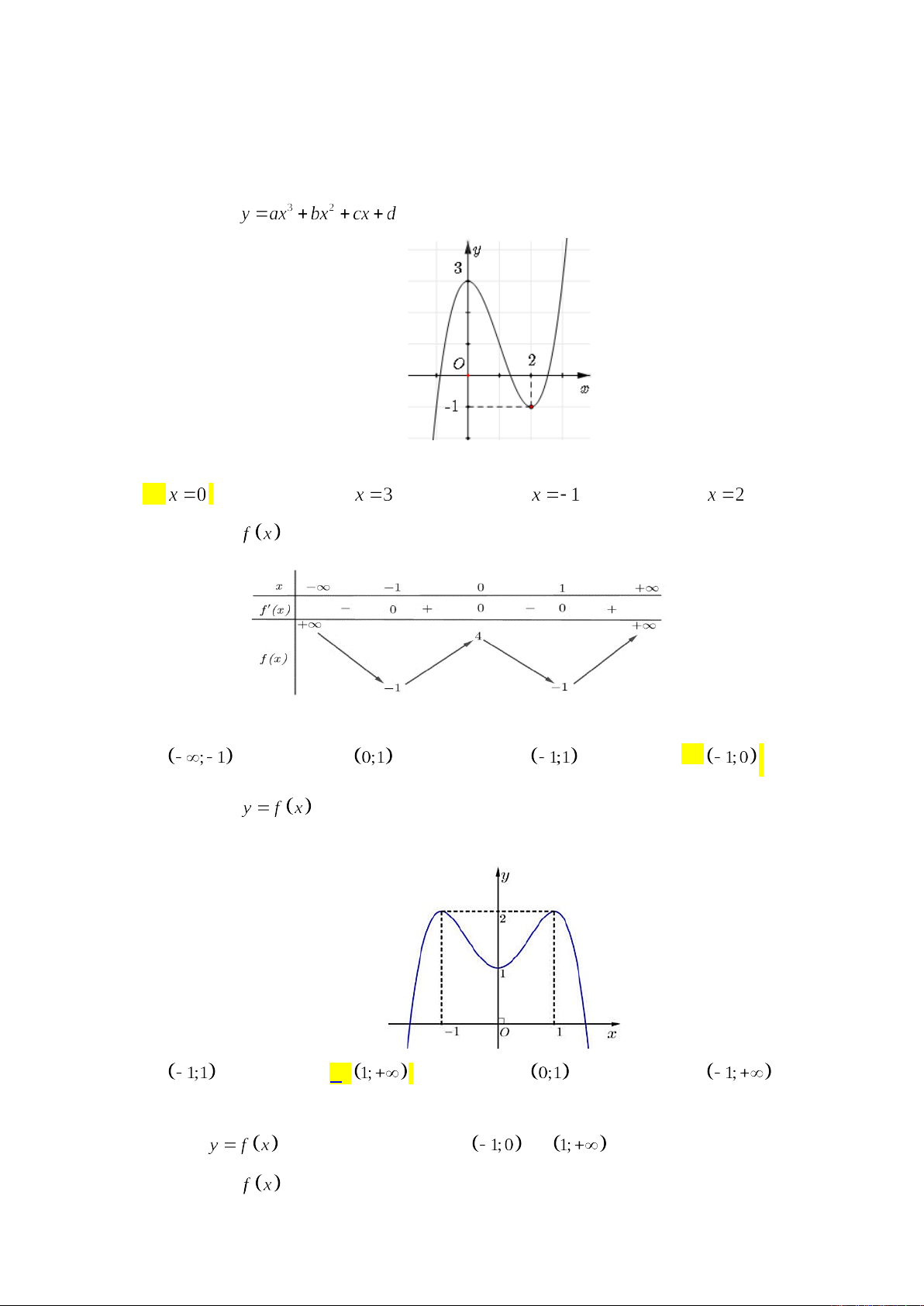
Câu 1. Cho hàm số có đồ thị là đường cong trong hình bên dưới.
Điểm cực đại của hàm số đã cho là
A. .B. .C. .D. .
Câu 2. Cho hàm số có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A. .B. .C. .D. .
Câu 3. Cho hàm số có đồ thị là đường cong hình bên dưới. Hàm số đã cho nghịch biến trên
khoảng nào dưới đây?
A. .B. .C. .D. .
Lời giải
Hàm số nghịch biến trên khoảng và .
Câu 4. Cho hàm số có bảng biến thiên như sau:
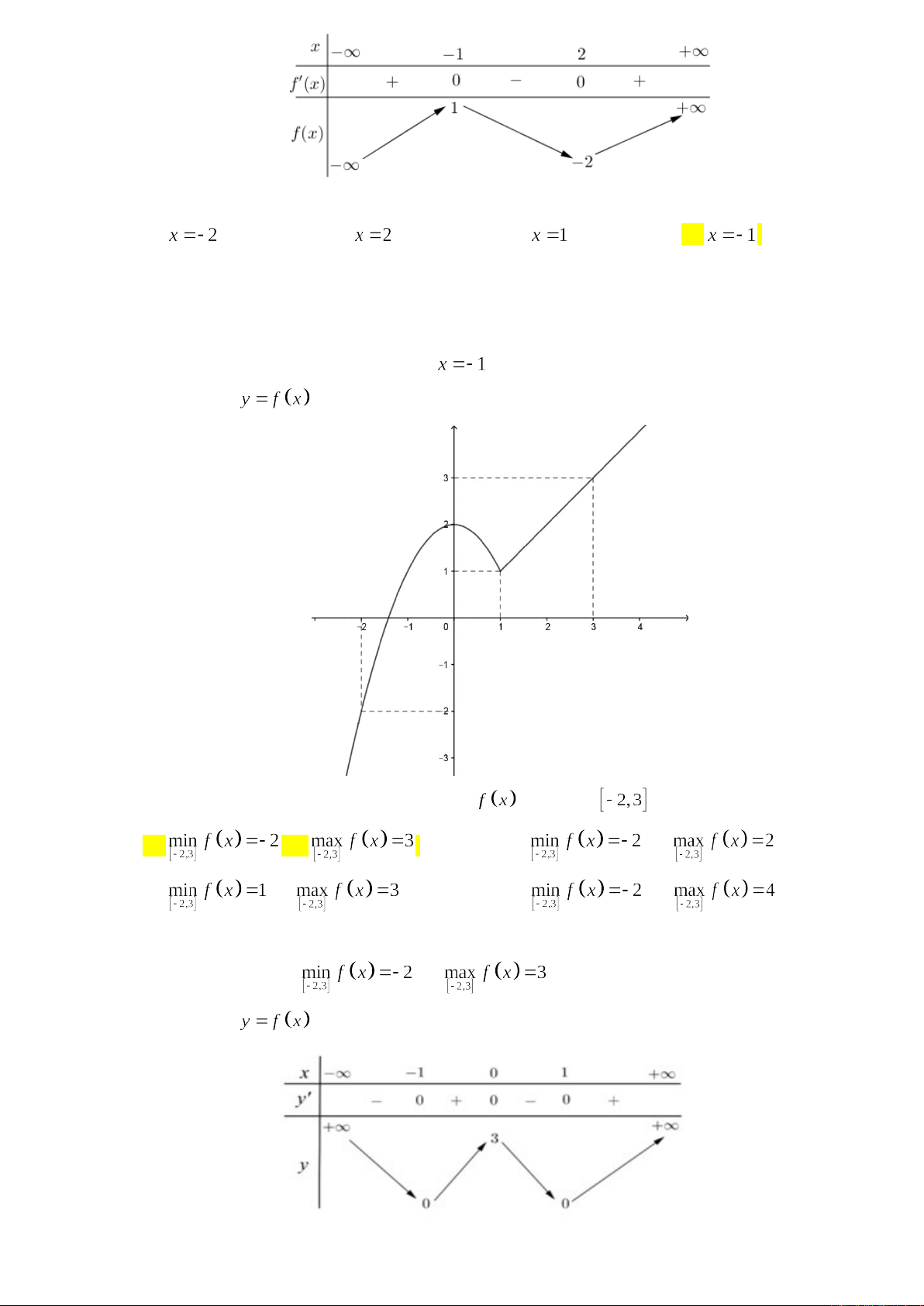
Hàm số đã cho đạt cực đại tại
A. .B. .C. .D. .
Lời giải
Chọn D
Hàm số đạt cực đại tại điểm mà đạo hàm đổi dấu từ dương sang âm.
Từ bảng biến thiên hàm số đạt cực đại tại .
Câu 5. Cho hàm số có đồ thị như hình dưới đây:
Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn ?
A. và . B. và .
C. và . D. và .
Lời giải
Dựa vào đồ thị ta có và .
Câu 6. Cho hàm số có bảng biến thiên như sau
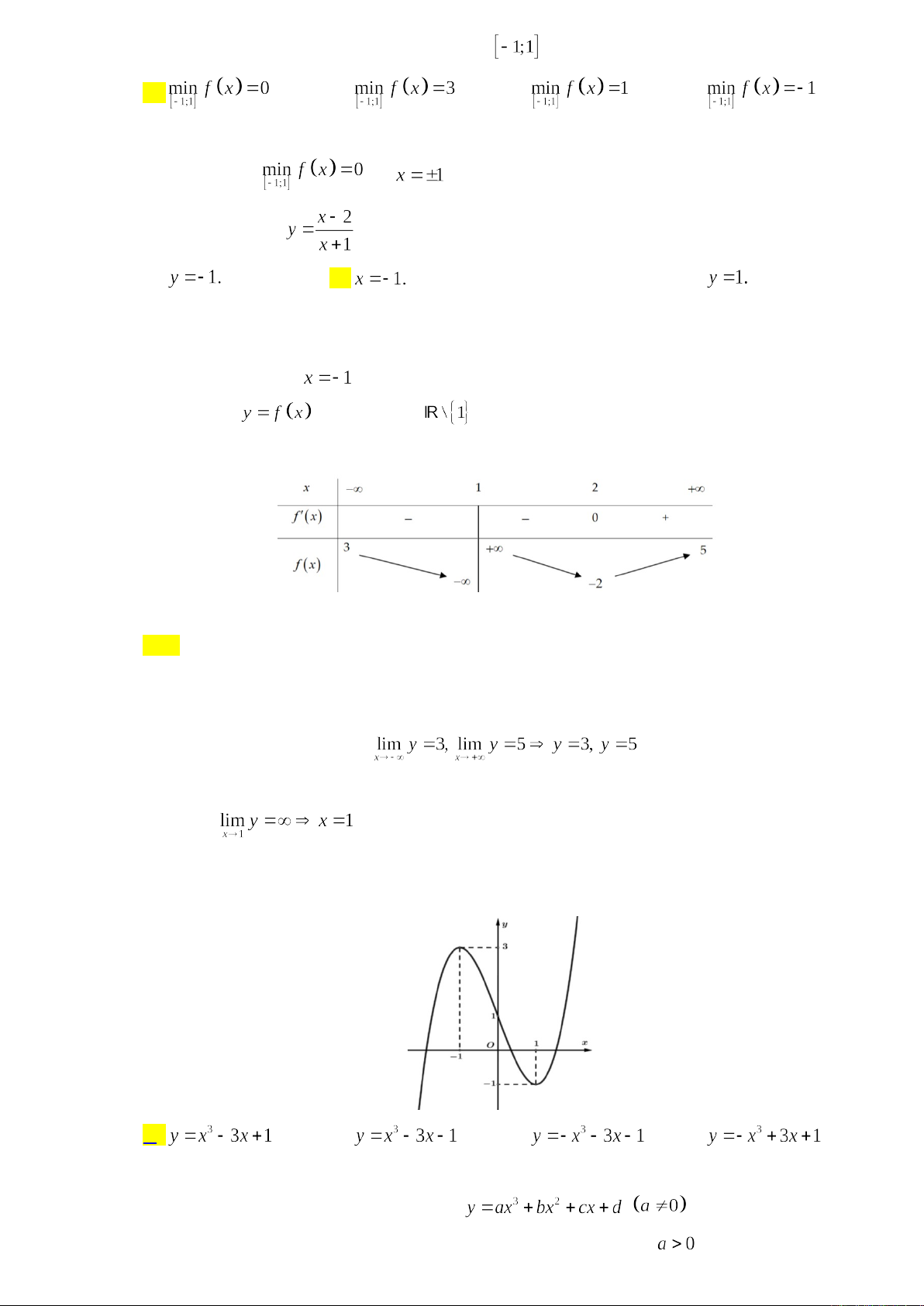
Cho biết giá trị nhỏ nhất của hàm số trên đoạn là bao nhiêu?
A. B. C. D.
Lời giải
Từ BBT suy ra tại .
Câu 7. Đồ thị của hàm số có đường tiệm cận đứng là
A. B. C.
1.x
D.
Lời giải
Chọn B
Ta có tiệm cận đứng .
Câu 8. Cho hàm số xác định trên liên tục trên mỗi khoảng xác định và có bảng biến
thiên sau.
Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?
A. 3. B. 4. C. 5. D. 2.
Lời giải
Chọn A
Dựa vào đồ thị hàm số ta thấy là 2 đường tiệm cận ngang
của đồ thị hàm số.
Mặt khác là tiệm cận đứng của đồ thị hàm số.
Do đó đồ thị hàm số có 3 đường tiệm cận.
Câu 9. Đồ thị sau đây là của hàm số nào?
A. .B. .C. .D. .
Lời giải
Đồ thị hàm số trên là đồ thị hàm số bậc ba .
Nhìn vào nhánh phải của đồ thị ta thấy đồ thị có hướng đi lên suy ra .
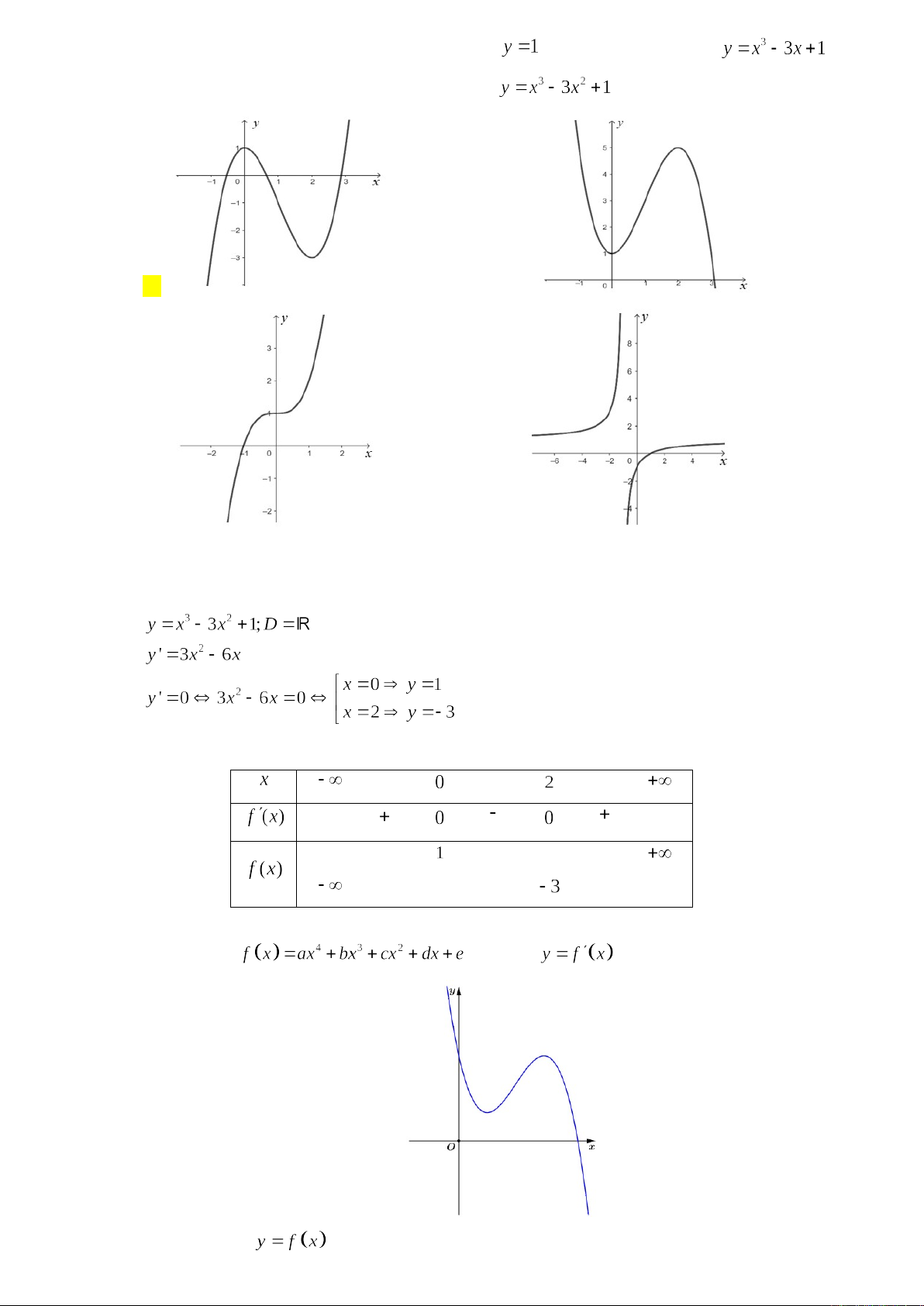
Đồ thị hàm số cắt trục tung tại điểm có tung độ . Vậy hàm số thỏa đề là .
Câu 10. Đường cong nào dưới đây là đồ thị của hàm số
A. .B. .
C. .D. .
Lời giải
Chọn A
Bảng biến thiên:
.
Câu 11. Cho hàm số . Hàm số có đồ thị như hình vẽ sau.
Đồ thị hàm số có tất cả bao nhiêu điểm cực trị?
A. .B. .C. .D. .
Lời giải
Ta có
Ta thấy đồ thị hàm số cắt đường thẳng tại điểm suy ra phương trình
có nghiệm đơn. Vậy hàm số có điểm cực trị.
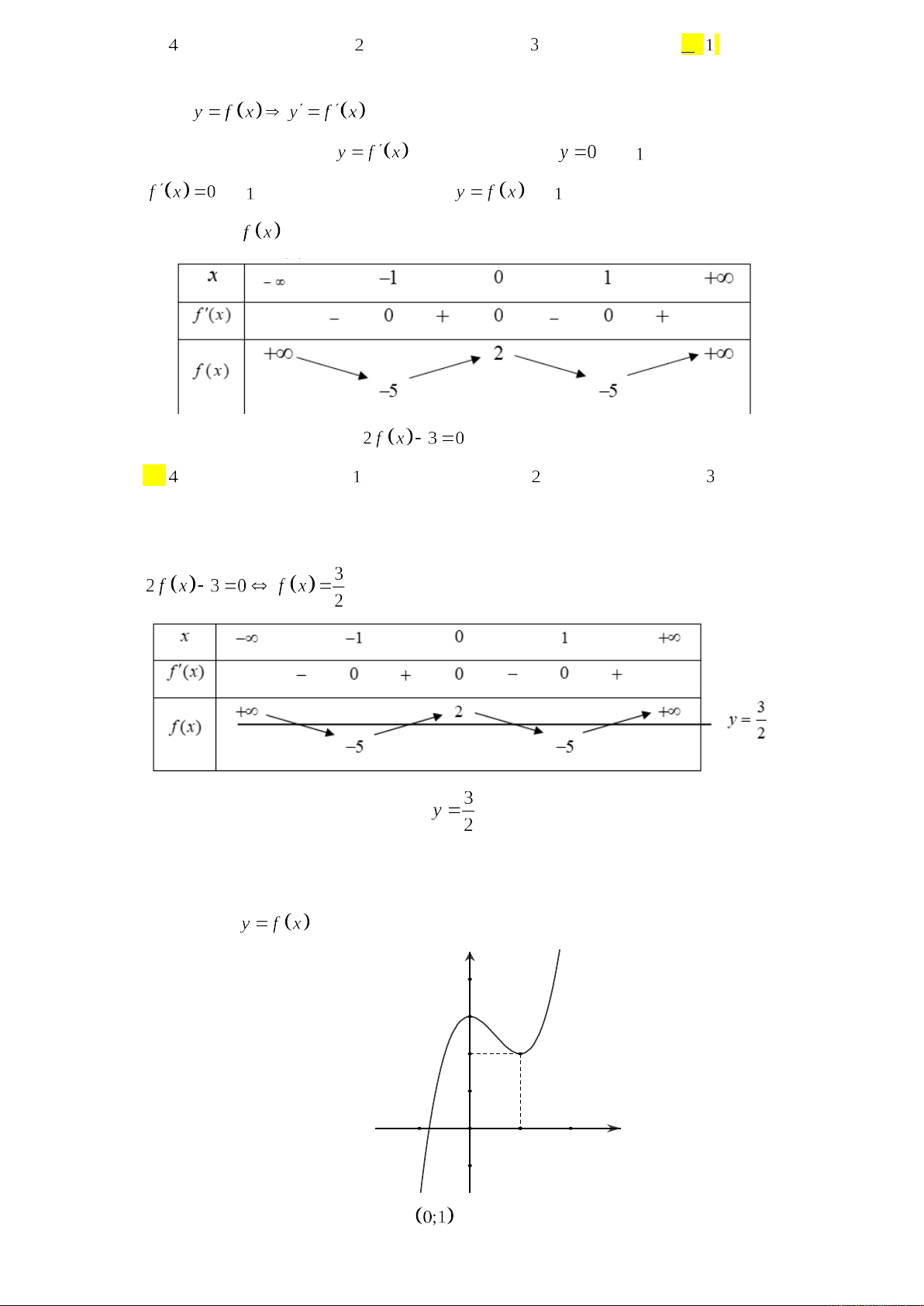
Câu 12. Cho hàm số có bảng biến thiên như sau:
Số nghiệm của phương trình là?
A. .B. .C. .D. .
Lời giải
Chọn A
.
Từ bảng biến thiên, thấy đường thẳng cắt đồ thị tại 4 điểm.
PHẦN II. Câu trắc nghiệm đúng sai. Trong mỗi ý A), B), C), D) ở mỗi câu, thí sinh chọn
đúng hoặc sai.
Câu 13. Cho hàm số có đồ thị như hình vẽ bên.
y
x
-1
-1
3
2
1
O
1
A. Hàm số nghịch biến trên khoảng .


























