A B C OR NOR AND NAND
0 0 0 0 1 0 1
0 0 1 1 0 0 1
0 1 0 1 0 0 1
0 1 1 1 0 0 1
1 0 0 1 0 0 1
1 0 1 1 0 0 1
1 1 0 1 0 0 1
1 1 1 1 0 1 0
Bài 1 : L p b ng ho t đ ng c a các c ng AND 3 ngõ vào , NAND 3 ngõ vào , OR 3 ngõ vào Và NOR 3ậ ả ạ ộ ủ ổ
ngõ vào
Bài 2 : v s đ m ch ẽ ơ ồ ạ
Y1 = A
Ta có A =
=>
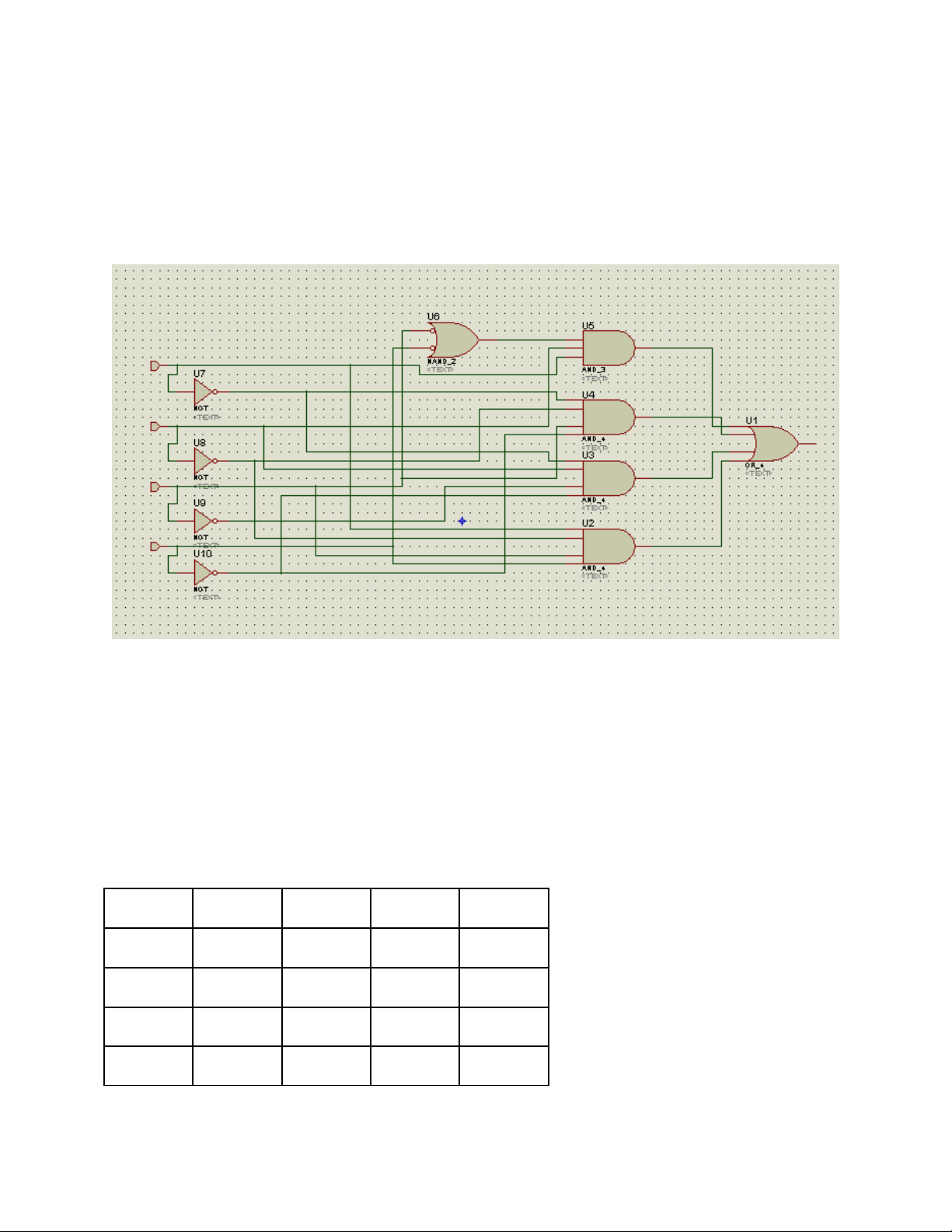
Y2 =
Bài 3 L p b ng ho t đ ng c a m ch s có ngõ ra sauậ ả ạ ộ ủ ạ ố
Y =
Ta có
Y =
A B C D Y
00001
00011
00101
00111
01001
01010
01101
01111
10001
10011
10101
10111
11000
11010
11101
11110
Bài 4
Y1 =
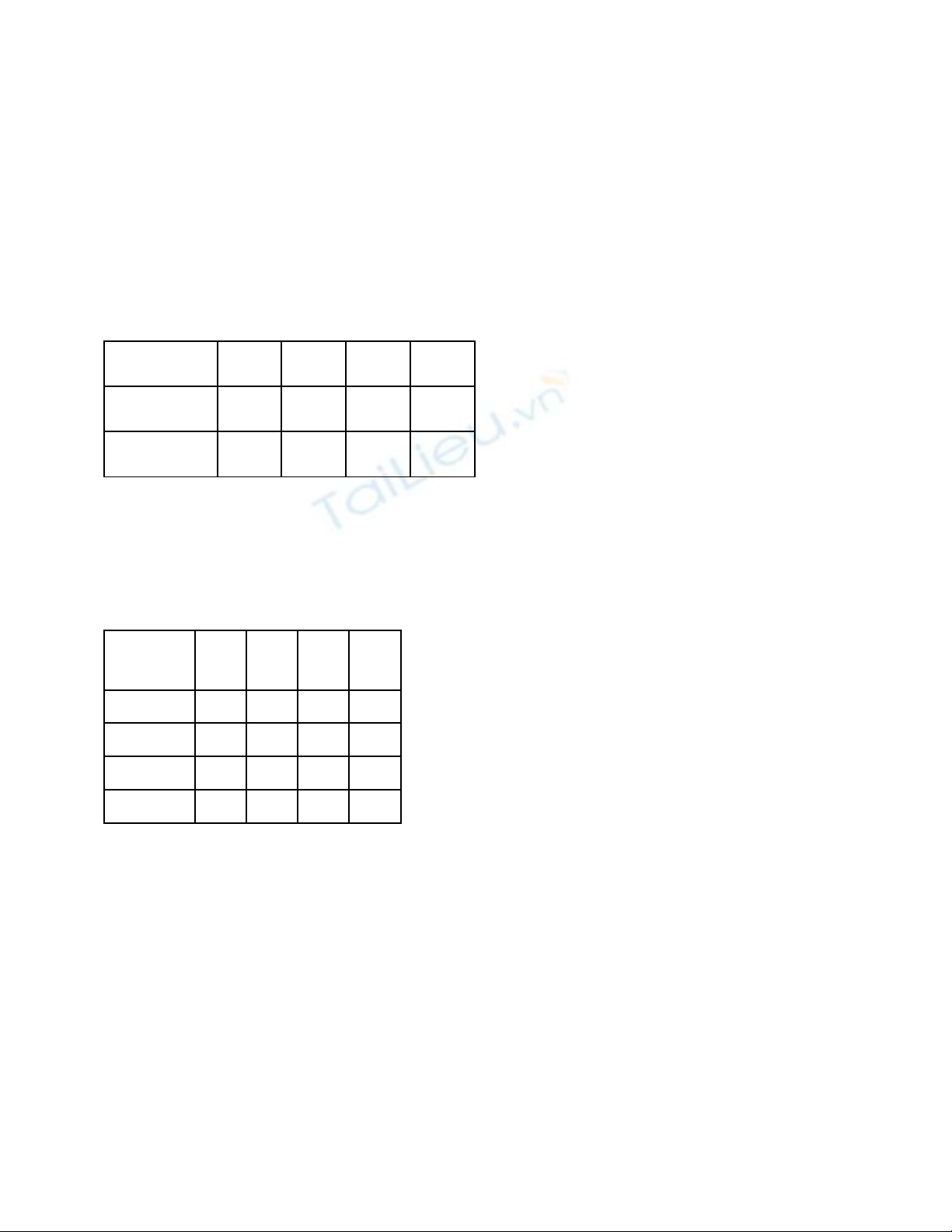
a. V s đ m chẽ ơ ồ ạ
b. L p b ng ho t đ ngậ ả ạ ộ
Y1= = = =
A C Y
0 0 1
0 1 1
1 0 1
1 1 0
Bài 5
f1 =
AB
C
00 01 11 10
0 1001
1 1001
f1 = A
f1=
A
B
DC
00 01 11 10
00 0 1 1 0
01 0 1 0 0
11 0 0 0 0
10 0 1 1 0
f2 =
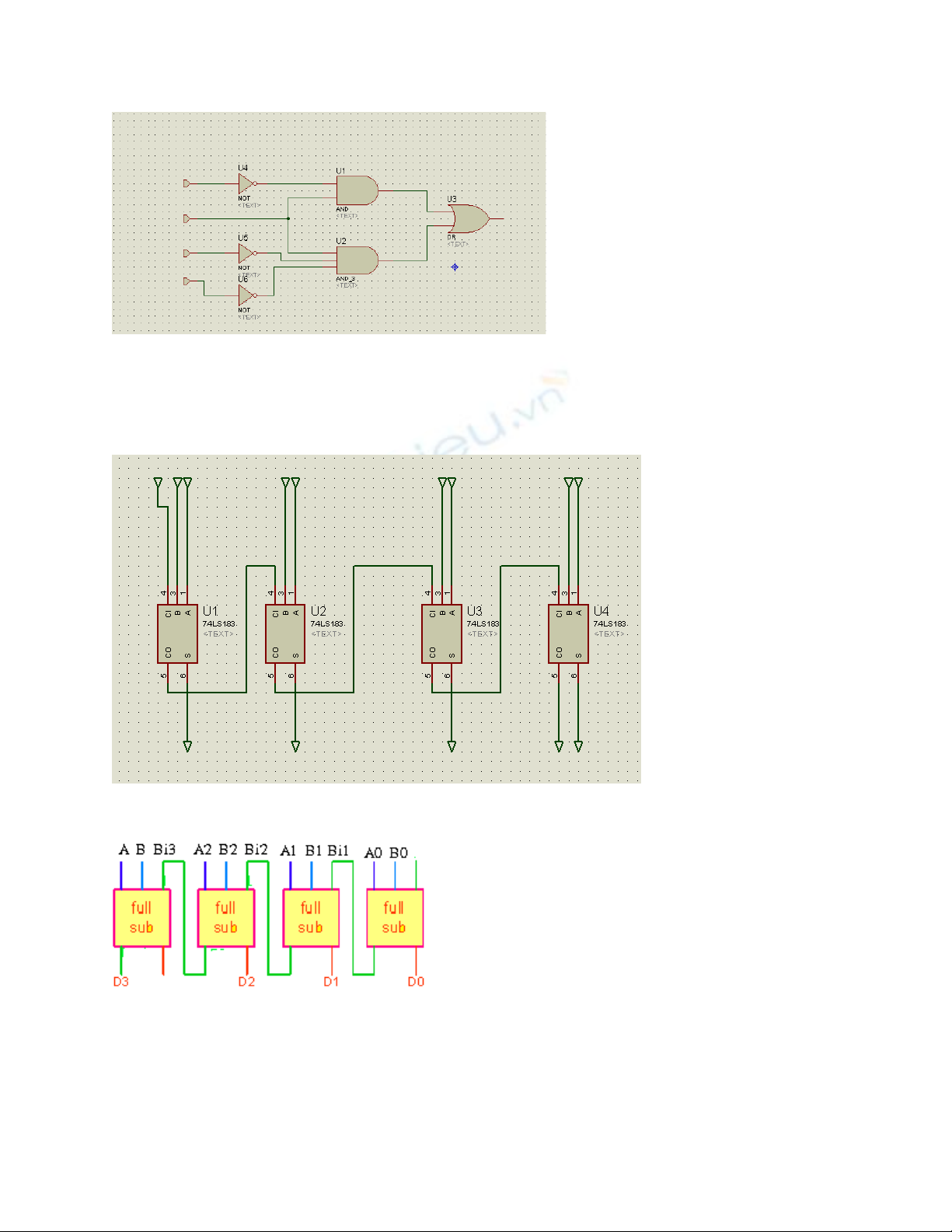
M ch c ng và m ch tr 4 bítạ ộ ạ ừ
+ M ch c ng 4 bitạ ộ
S d ng 4 full-adder :ử ụ
+ M ch tr 4 bitạ ừ