BÀI T P K THU T SẬ Ỹ Ậ Ố
Ch ng 1: Các h th ng s đ mươ ệ ố ố ế
1.1 Bi u di n các s sau trong h nh phân (binary)ể ễ ố ệ ị
a. 23
b. 14
c. 27
d. 34
1-2 Bi u di n các s sau trong h nh phân (binary)ể ễ ố ệ ị
a. 23H
b. 14H
c. C06AH
d. 5DEFH
1.3 Bi u di n các s sau trong h th p phân (decimal)ể ễ ố ệ ậ
a. 01101001B
b. 01111111B
c. 1FH
d. 10H
1.4 Bi u di n các s sau trong h th p l c phân (hex)ể ễ ố ệ ậ ụ
a. 100
b. 10110001B
c. 111100101011100000B
d. 256
1.5 Bi u di n các s cho bài ể ễ ố ở 1-1 và 1-3 thành h th p l c phân (hex).ệ ậ ụ
1.6 Bi u di n các s cho bài ể ễ ố ở 1-2 và 1-6 thành h th p phân (decimal).ệ ậ
1.7 Bi u di n các s cho bài ể ễ ố ở 1-4 và 1-5 thành h nh phân (binary).ệ ị
1.8 Đ i các s sau sang h nh phânổ ố ệ ị
a. 27,625
b. 12,6875
c. 6,345
d. 7,69
1.9 Đ i các s sau sang h bát phân (octal)ổ ố ệ
a. 1023H
b. ABCDH
c. 5EF,7AH
d. C3,BF2H
1.10 L y bù 1 các s sauấ ố
a. 01111010B
b. 11101001B
c. 00000000B
d. 11111111B
1.11 L y bù 2 các s sauấ ố
a. 10101100B
b. 01010100B
c. 00000000B
d. 11111111B
1.12 L y bù 9 các s sauấ ố
a. 3
b. 14
c. 26
d. 73
1.13 L y bù 10 các s sauấ ố
a. 7
b. 25
c. 62
d. 38
1.14 Cho các s nh phân có d u sau, hãy tìm giá tr c a chúngố ị ấ ị ủ
a. 0111B
b. 1000B
c. 0000B
d. 1111B
1.15 Bi u di n các s sau thành mã BCD (còn g i là mã BCD 8421 hay mã BCDể ễ ố ọ
chu n)ẩ
a. 2
b. 9
c. 10
d. 255
1.16 Làm l i bài ạ1-21, nh ng đ i thành mã BCD 2421 (còn g i là mã 2421)ư ổ ọ
1.17 Làm l i bài ạ1-21, nh ng đ i thành mã BCD quá 3 (còn g i là mã quá 3 – XS3)ư ổ ọ
1.18 Cho các mã nh phân sau, hãy đ i sang mã Grayị ổ
a. 0111B
b. 1000B
c. 01101110B
d. 11000101B
1.19 Cho các mã nh phân sau, hãy xác đ nh giá tr c a chúng n u chúng là (i) s nhị ị ị ủ ế ố ị
phân không d u; (ii) s nh phân có d u; (iii) mã BCD; (iv) mã 2421; (v) mã quá 3;ấ ố ị ấ
(vi) mã Gray
a. 1000011B
b. 110101B
c. 1101100B
d. 01000010B
Ch ng 2: Đ i s Booleươ ạ ố
2-1 Ch ng minh các đ ng th c sau b ng đ i sứ ẳ ứ ằ ạ ố
a.
))()(( DBCADADCBDABA +++=++
b.
))()(( DBCBCABDACBDC +++=++
c.
))(( ZYZXZXXYZ ++=++
d.
BABA ⊕=⊕
e.
ABCCBAAB =⊕⊕ )(
2-2 Cho b ng chân tr sauả ị
C B A F1 F2
0 0 0 0 1
0 0 1 0 0
0 1 0 1 0
0 1 1 0 1
1 0 0 0 1
1 0 1 1 1
1 1 0 0 1
1 1 1 1 0
a. Vi t bi u th c c a hàm F1 và F2ế ể ứ ủ
b. Vi t bi u th c hàm F1 d i d ng tích các t ng (POS)ế ể ứ ướ ạ ổ
c. Vi t bi u th c hàm F2 d i d ng t ng các tích (SOP)ế ể ứ ướ ạ ổ
d. Vi t hàm F1 d i d ng Σ và Πế ướ ạ
e. Vi t hàm F2 d i d ng Σ và Πế ướ ạ
2-3 Cho b ng chân tr sauả ị
A B C F1 F2
0 0 0 1 1
0 0 1 0 X
0 1 0 X 0
0 1 1 0 1
1 0 0 0 1
1 0 1 1 X
1 1 0 X X
1 1 1 0 0
a. Vi t bi u th c các hàm F1 và F2ế ể ứ
b. Vi t d ng Σ và Π cho hàm F1 và F2ế ạ
2-4 Cho các hàm sau
))()((),,,(
.),,,(
2
1
DBDCADCBDCBAF
CAACDDBADBCADCBAF
+++++=
+++=
Hãy l p b ng chân tr c a F1 và F2ậ ả ị ủ
2-5 Cho các hàm sau
∏
∑
=
+=
)8,7,6,0().15,14,12,11,5,4,3,1(),,,(
)15,13,3()12,8,6,4,2,1,0(),,,(
2
1
dDCBAF
dDCBAF
Hãy l p b ng chân tr c a F1 và F2ậ ả ị ủ
2-6 Cho gi n đ xung sauả ồ
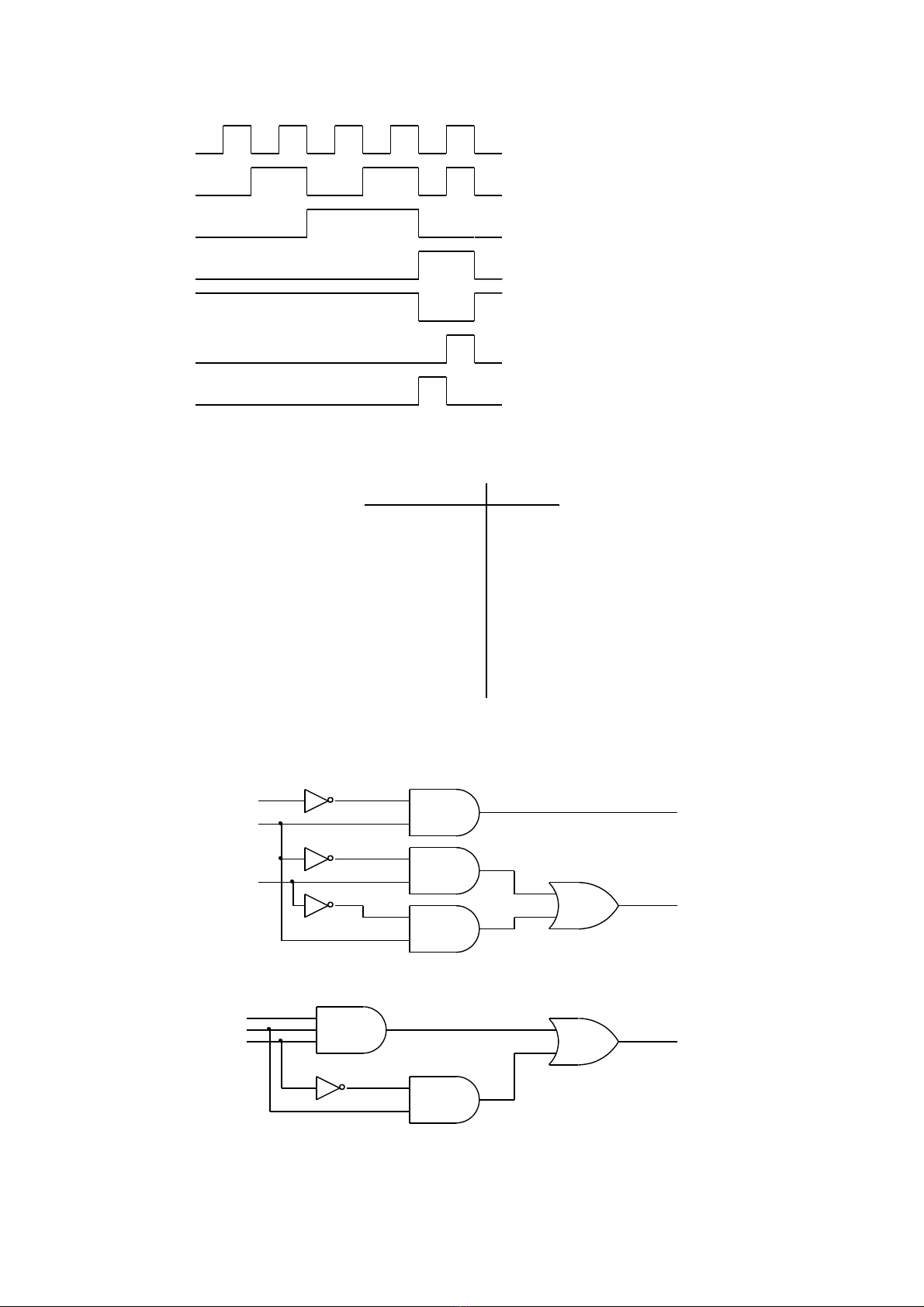
a. Vi t bi u th c các hàm F1, F2 và F3ế ể ứ
b. Vi t d ng Σ và Π cho hàm F1, F2 và F3ế ạ
2-7 Cho b ng chân tr sauả ị
A B C D F1 F2
0 0 0 0 1 1
0 0 0 1 0 1
0 0 1 0 0 0
0 0 1 1 0 1
0 1 0 0 1 1
0 1 0 1 0 1
0 1 1 0 0 0
0 1 1 1 0 1
1 X X X 1 0
a. Vi t bi u th c các hàm F1 và F2ế ể ứ
b. Vi t d ng Σ và Π cho hàm F1 và F2ế ạ
2-8 Bi u di n các hàm đã cho trong các bài t ể ễ ừ 2-2 đ n ế2-7 trên bìa Karnaugh
2-9 Cho s đ m ch sau, hãy vi t bi u th c chu n 1 và 2 c a F1 và F2ơ ồ ạ ế ể ứ ẩ ủ
Y
Z
F 1
F 2
X
2-10 Cho s đ m ch và gi n đ xung các tín hi u vào nh sau, hãy v d ng tínơ ồ ạ ả ồ ệ ư ẽ ạ
hi u F.ệ
A
B
C
D
F1
F2
F3
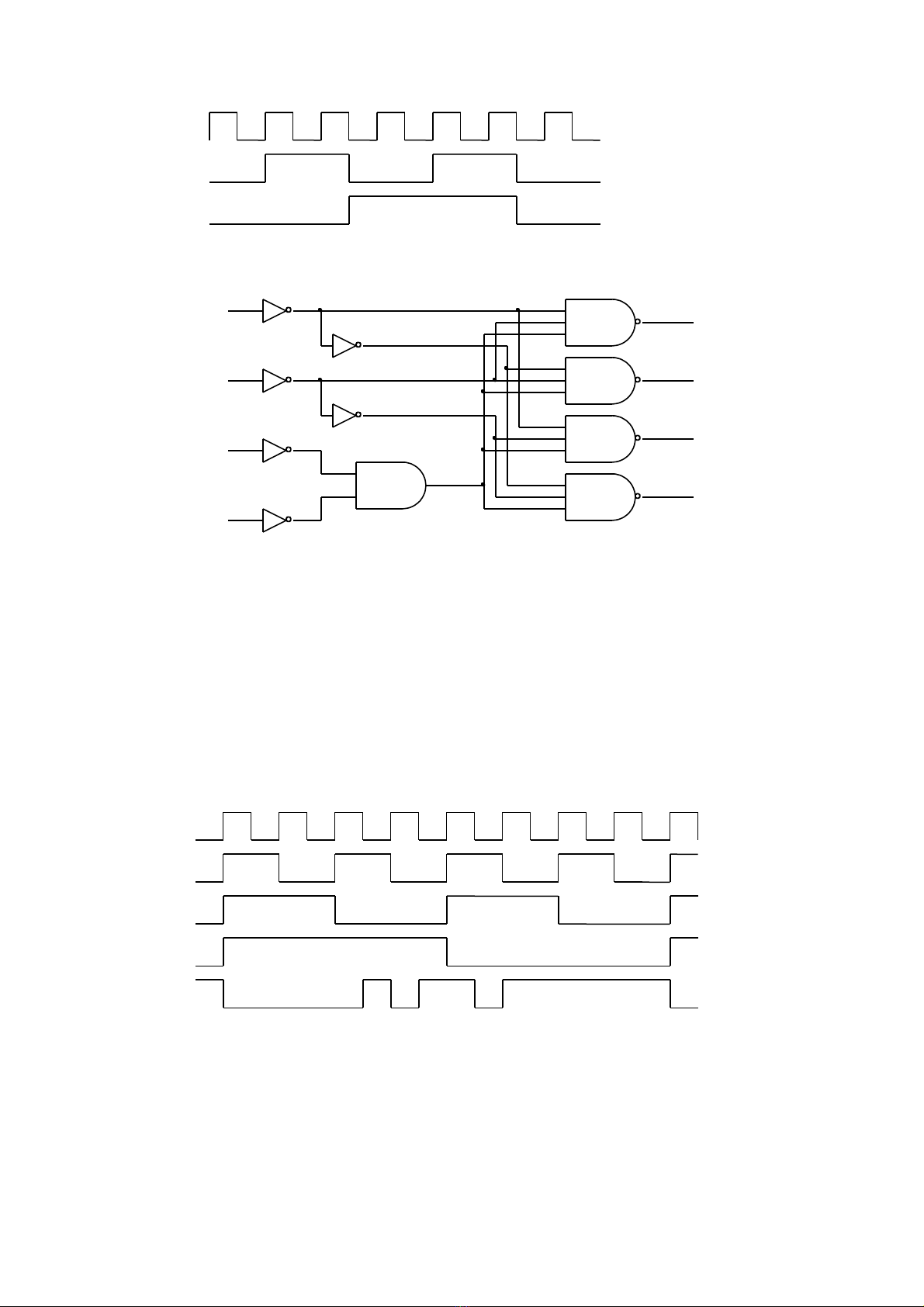
2-11 Cho s đ m ch nh sauơ ồ ạ ư
A
B
E
D
Y 1
Y 3
Y 2
Y 0
L p b ng chân tr và vi t các hàm trong các tr ng h p sauậ ả ị ế ườ ợ
a. E=0 và D=0
b. E=0
2-14 Dùng bìa Karnaugh rút g n các hàm sauọ
)5,3()15,9,7,4,2,1(),,,(
1dDCBAF += ∑
∑
=)15,14,11,10,8,5,4,2,1,0(),,,(
2DCBAF
)10,0(.)15,13,8,7,5,2(),,,(
3dDCBAF ∏
=
∏
=)13,12,10,8,6,5,4,2,0(),,,(
4DCBAF
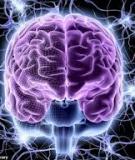
2-15 Cho hàm F(A,B,C,D) bi u di n trên gi n đ xung nh sauể ễ ả ồ ư
a. Vi t bi u th c chu n 2 c a hàm Fế ể ứ ẩ ủ
b. Bi u di n hàm trên bìa Karnaughể ễ
c. Rút g n hàm F và v m ch th c hi n ch dùng c ng NANDọ ẽ ạ ự ệ ỉ ổ
2-16 Rút g n hàm sau và th c hi n b ng c ng NAND 2 ngõ vàoọ ự ệ ằ ổ
)13,11,8()14,12,10,9,6,4(),,,( dDCBAF += ∑
2-17 Rút g n hàm sau và th c hi n b ng c ng NOR 2 ngõ vàoọ ự ệ ằ ổ
)15,13,7(.)11,10,9,6,4,3,2,0(),,,( dDCBAF ∏
=
A
B
C
A
B
C
D
F