intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

Bài tập Kỹ thuật số Chương 2

Chia sẻ: Nguyễn Văn Nguyên | Ngày: | Loại File: PDF | Số trang:16

Thêm vào BST
Báo xấu
120
lượt xem 16
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

Biến đổi các số nhị phân sau sang thập phân: a) 101102 b) 100011012 c) 1001000010012 d) 11110101112 e) 101111112 f) 1100011012 2. Biến đổi các số thập phân sau số nhị phân: a) 37 b) 14 c) 189 d) 205 e) 2313 f) 511 3. Biến đổi các số bát phân sau sang nhị phân: a) 478 b) 238 c) 1708 d) 2068 e) 23138 f) 6168 4. Biến đổi các số thập lục phân sau sang nhị phân: a) AF16 b) 1A216 c) 23416 d) 12A416 e) BC1216 f) 51716 5. Biến đổi các số thập phân sau...

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài tập Kỹ thuật số Chương 2

  1. Baøi taäp Kyõ thuaät soá Chöông 2 Baøi taäp chöông 2 1. Bieán ñoåi caùc soá nhò phaân sau sang thaäp phaân: a) 101102 b) 100011012 c) 1001000010012 d) 11110101112 e) 101111112 f) 1100011012 2. Bieán ñoåi caùc soá thaäp phaân sau soá nhò phaân: a) 37 b) 14 c) 189 d) 205 e) 2313 f) 511 3. Bieán ñoåi caùc soá baùt phaân sau sang nhò phaân: a) 478 b) 238 c) 1708 d) 2068 e) 23138 f) 6168 4. Bieán ñoåi caùc soá thaäp luïc phaân sau sang nhò phaân: a) AF16 b) 1A216 c) 23416 d) 12A416 e) BC1216 f) 51716 5. Bieán ñoåi caùc soá thaäp phaân sau sang baùt phaân: a) 111 b) 97 c) 234 d) 45 e) 3214 f) 517 6. Bieán ñoåi caùc soá thaäp phaân sau sang thaäp luïc phaân: a) 22 b) 321 c) 2007 d) 123 e) 4234 f) 517 7. Bieán ñoåi caùc soá nhò phaân sau sang baùt phaân: a) 10111001012 b) 1001110000112 c) 1110001112 d) 10000100112 e) 1100101001012 f) 1000111002 8. Bieán ñoåi caùc soá nhò phaân trong baøi 7 sang thaäp luïc phaân: 9. Bieán ñoåi caùc soá baùt phaân sau sang thaäp luïc phaân: a) 7438 b) 368 c) 37778 d) 2578 e) 12048 f) 14328 10. Bieán ñoåi caùc soá thaäp luïc phaân trong baøi 4 sang baùt phaân: 11. Bieán ñoåi caùc soá nhò phaân sau sang thaäp phaân: a) 101110.01012 b) 100111000.0112 c) 111000.1112 d) 100001.00112 e) 110010100.1012 f) 100011.1002 12. Maõ hoùa caùc soá thaäp phaân sau sang BCD: a) 47 b) 962 c) 187 d) 1204 e) 187 f) 822 1
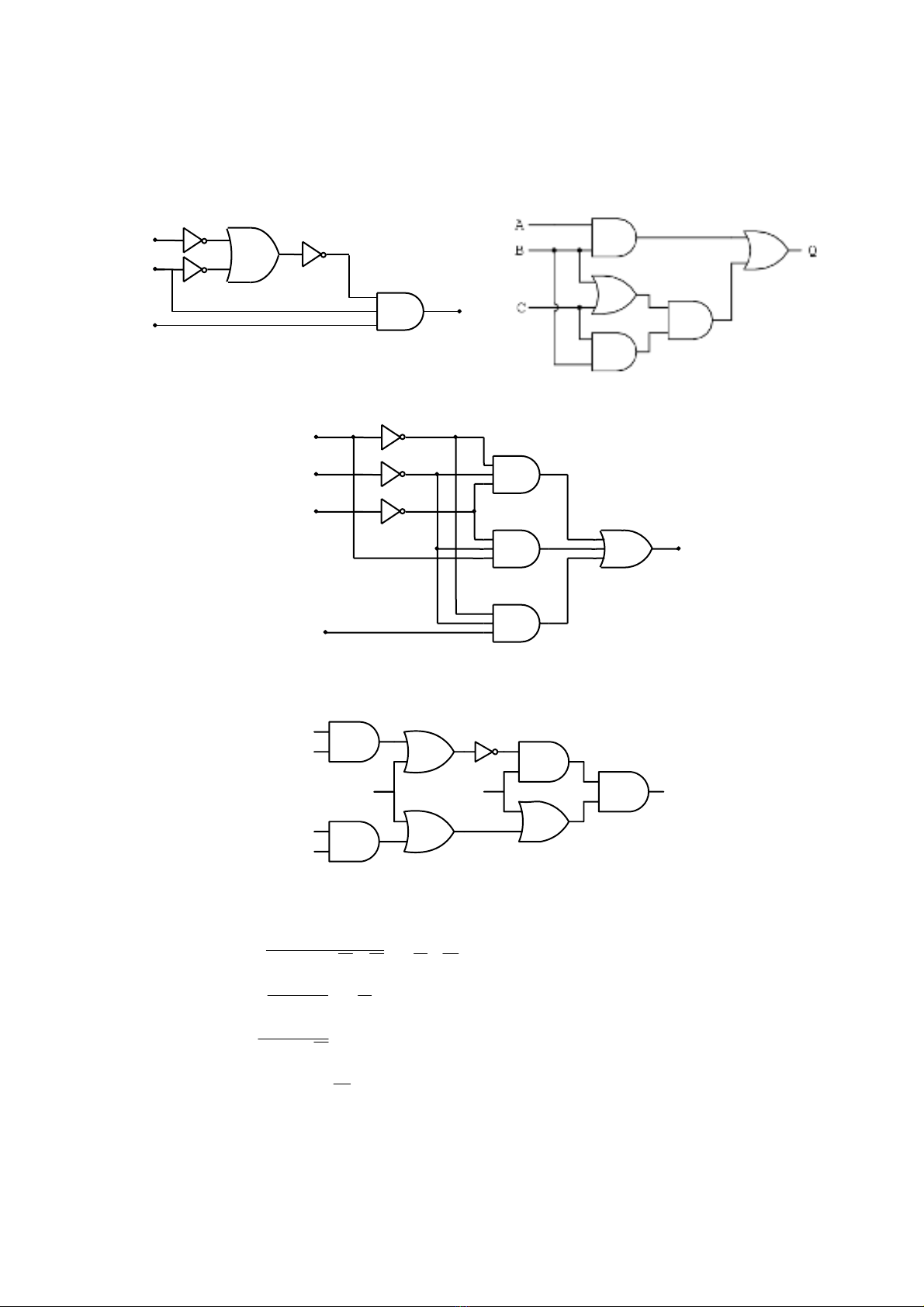
  2. Baøi taäp Kyõ thuaät soá Chöông 3 Baøi taäp chöông 3 1. Xaùc ñònh bieåu thöùc Boolean vaø baûng chaân trò cho caùc maïch sau ñaây. A B X C (a) (b) A B C X D (c) A B C D F A B (d) 2. Veõ sô ñoà maïch cho caùc bieåu thöùc sau ñaây, chæ söû duïng coång AND, OR vaø NOT. a. x = ( A + B + C D E ) + BC D b. y = ( M + N ) + PQ c. z = W + P Q d. t = MN ( P + N ) Trang 1
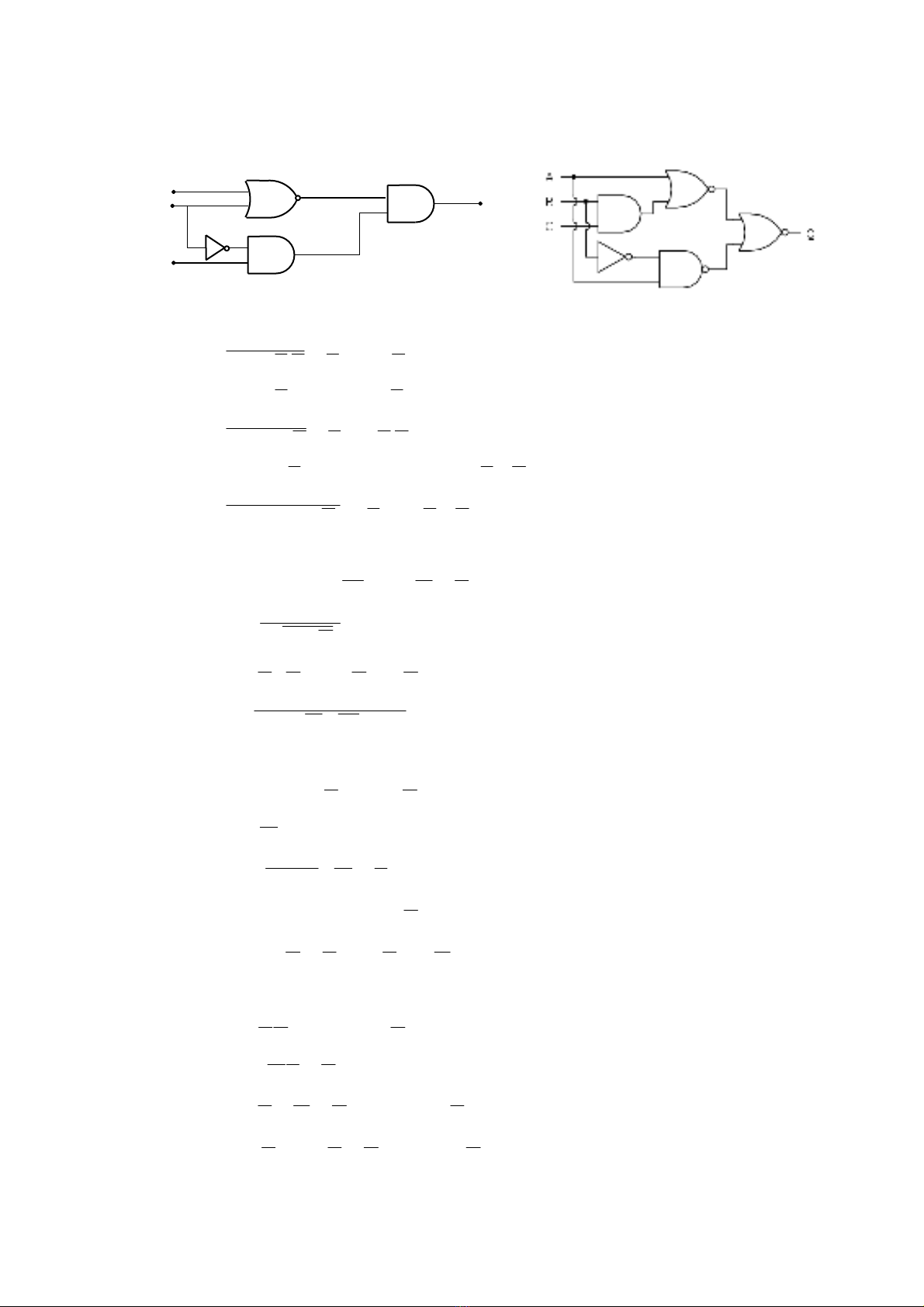
  3. Baøi taäp Kyõ thuaät soá Chöông 3 3. Xaùc ñònh bieåu thöùc Boolean vaø baûng chaân trò cho caùc maïch sau ñaây. A X B C (a) (b) 4. Ch ứ ng minh bằng đại số các biểu thức sau: a. A.B + A.B = A.B + A.B ( ) b. A.B + A.C = ( A + C ) A + B A.C + B.C = A.C + B.C c. (A + B )(A + C )(B + C ) = (A + B )(A + C ) d. ( A + C )(B + C ) = (A + C )(B + C ) e. 5. Ñôn giaûn caùc bieåu thöùc Boolean sau: a. x = ( M + N )( M + P )( N + P ) b. y = A( B + C )D c. z = ABC + ABC + BC D d. t = ( M + N )( M + N ) 6. Ñôn giaûn caùc bieåu thöùc Boolean sau: a. x = ABC + AB + ABC b. y = X YZ + XZ c. z = ( X + Y )( X + Y ) d. t = XY + X (WZ + W Z ) e. m = ( BC + AD )( A B + C D ) 7. Ñôn giaûn caùc bieåu thöùc Boolean sau: a. x = AC + ABC + AC b. y = ( X Y + Z ) + Z + XY + WZ c. z = AB ( D + C D ) + B ( A + ACD ) d. t = ( A + C )( A + C )( A + B + C D ) Trang 2
  4. Baøi taäp Kyõ thuaät soá Chöông 3 8. Haõy söû duïng coång NAND 2 ngoõ vaøo ñeå laøm moät maïch logic töông ñöông vôùi coång NOR 2 ngoõ vaøo. (Caùch ñôn giaûn nhaát) 9. Haõy söû duïng coång NOR 2 ngoõ vaøo ñeå laøm moät maïch logic töông ñöông vôùi coång NAND 2 ngoõ vaøo. (Caùch ñôn giaûn nhaát). 10. Tìm buø cuûa caùc bieåu thöùc sau ñaây: a. x = X Y + X Y b. y = ( A B + C ) D + E c. z = AB (C D + C D ) + A B (C + D )(C + D ) d. t = ( X + Y + Z )( X + Z )( X + Y ) Trang 3
  5. Baøi taäp Kyõ thuaät soá Chöông 4 Baøi taäp chöông 4 1. Theå hieän caùc bieåu thöùc sau ñaây döôùi daïng chuaån taéc tuyeån vaø chuaån taéc hoäi. a) f ( A, B, C ) = 1 neáu soá nhò phaân (ABC)2 laø soá chaün. b) f ( A, B, C ) = 1 neáu coù ít nhaát hai bieán soá baèng 1. c) f ( A, B, C ) = 1 neáu soá nhò phaân (ABC)2 > 5. 2. Ñôn giaûn caùc bieåu chöùc sau baèng phöông phaùp söû duïng ñaïi soá Boolean: ( ) a) q = RST R + S + T b) x = ABC + AC ( )( ) c) z = B + C B + C + A + B + C d) y = (Q + R )(Q + R ) 3. Ñôn giaûn caùc bieåu chöùc sau baèng phöông phaùp söû duïng ñaïi soá Boolean: a) x = A B C + ABC + ABC + A B C + A BC b) w = ABC + A BC + A ( ) c) y = C + D + AC D + A B C + A BCD + AC D () d) z = ABC + AB AC 4. 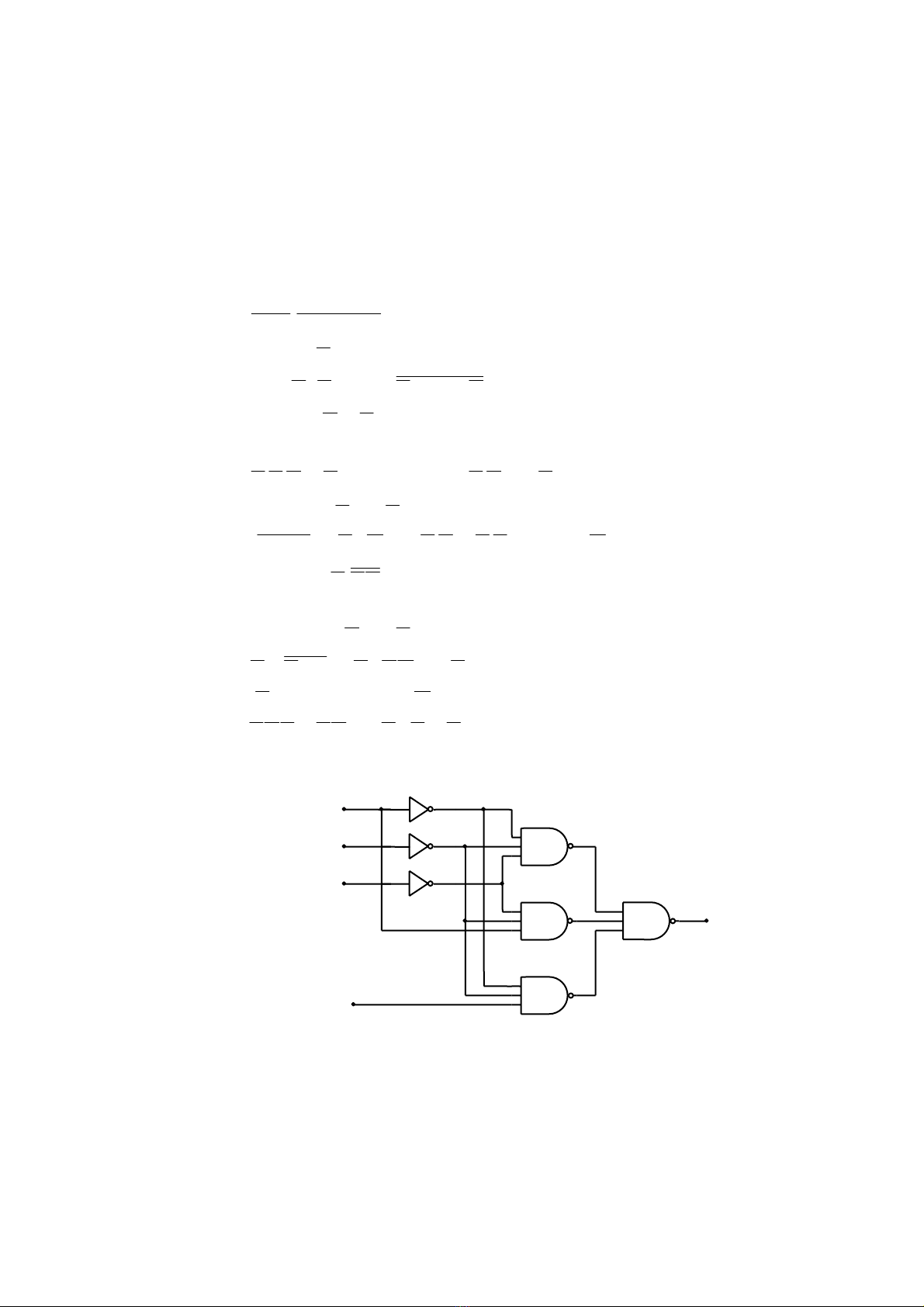Ñôn giaûn caùc bieåu chöùc sau baèng phöông phaùp söû duïng ñaïi soá Boolean: a) z = ABC + ABC + A BC () b) z = AC ABD + ABC D + A BC ( ) c) x = A + B ( A + B + D )D d) s = PQ R + PQR + PQ R + PQR + PQR 5. Söû duïng ñaïi soá Boolean ñeå ñôn giaûn maïch logic sau: A B C X D 6. Haõy thieát keá moät heä thoáng coù 3 ngoõ vaøo vaø 1 ngoõ ra, ngoõ ra ôû traïng thaùi “1” chæ khi coù soá leõ ngoõ vaøo ôû traïng thaùi “1”. 7. Thieát keá moät maïch toå hôïp coù 3 ngoõ vaøo vaø moät ngoõ ra. Ngoõ ra baèng logic 1 khi giaù trò thaäp phaân cuûa ngoõ vaøo nhoû hôn 3, trong tröôøng hôïp ngöôïc laïi ngoõ ra baèng logic 0 Trang 1
  6. Baøi taäp Kyõ thuaät soá Chöông 4 8. Thieát keá maïch logic cho baûng chaân trò sau: A B C X 0 0 0 1 0 0 1 0 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 0 1 1 0 0 1 1 1 1 9. Haõy thieát keá moät heä thoáng coù 4 ngoõ vaøo A, B, C, D vaø 1 ngoõ ra, ngoõ ra ôû traïng thaùi “1” chæ khi A = B = 1 hoaëc khi C = D = 1. 10. Thieát keá maïch logic coù boán ngoõ vaøo maø ngoõ ra cuûa noù ôû möùc cao chæ khi coù ít nhaát 2 ngoõ vaøo ôû traïng thaùi thaáp. 11. Thieát keá moät maïch toå hôïp coù 3 ngoõ vaøo X, Y, Z vaø 3 ngoõ ra a, b, c. Khi giaù trò thaäp phaân cuûa ngoõ vaøo baèng 0, 1, 2, 3 thì giaù trò thaäp phaân ngoõ ra lôùn hôn giaù trò ngoõ vaøo moät ñôn vò. Khi giaù trò thaäp phaân cuûa ngoõ vaøo laø 4, 5, 6, 7 thì giaù trò thaäp phaân ngoõ ra nhoû hôn giaù trò ngoõ vaøo 1 ñôn vò. ÑS: a = XY + XZ + YZ ; b = X ⊕ Y ⊕ Z ; c = Z 12. Ñôn giaûn caùc bìa Karnaugh sau: a) b) c) d) e) f) Trang 2
  7. Baøi taäp Kyõ thuaät soá Chöông 4 13. Ñôn giaûn caùc bìa Karnaugh sau: a) b) c) 14. Toái thieåu caùc bieåu thöùc sau (laøm taát caû caùc tröôøng hôïp coù theå): a. g ( X , Y , Z ) = ∑ (1, 2, 3, 4, 6, 7 ) f (W , X , Y , Z ) = ∑ (2, 5, 7, 8, 10, 12, 13, 15) b. c. g ( A, B, C , D ) = ∑ (0, 6, 8, 9, 10, 11, 13, 14, 15) (2 lôøi giaûi) f ( A, B, C , D ) = ∑ (0, 4, 5, 6, 7, 8, 9, 10, 11, 13, 14, 15) d. (2 lôøi giaûi) f ( A, B, C , D ) = ∑ (0, 1, 2, 4, 6, 7, 8, 9, 10, 11, 12, 15) e. 15. Toái thieåu caùc bieåu thöùc sau (laøm taát caû caùc tröôøng hôïp coù theå): a. g ( A, B, C , D ) = ∑ (0, 2, 3, 5, 7, 8, 10, 11, 12, 13, 14, 15) (4 lôøi giaûi) b. m( A, B, C , D ) = ∑ (0, 1, 4, 5, 7, 8, 10, 13, 14, 15) (3 lôøi giaûi) f (W , X , Y , Z ) = ∑ (2, 3, 4, 5, 6, 7, 9, 10, 11, 13) c. d. h( A, B, C , D ) = ∑ (1, 2, 3, 4, 8, 9, 10, 12, 13, 14, 15) (2 lôøi giaûi) 16. Toái thieåu caùc bieåu thöùc sau (laøm taát caû caùc tröôøng hôïp coù theå): a. f ( A, B, C , D ) = ∑ (0, 2, 3, 7, 8, 9, 13, 15) vôùi N = 1, 12 f (W , X , Y , Z ) = ∑ (1, 3, 5, 6, 7, 13, 14 ) vôùi N = 8, 10, 12 b. (2 lôøi giaûi) f ( A, B, C , D ) = ∑ (3, 8, 10, 13, 15) vôùi N = 0, 2, 5, 7, 11, 12, 14 (8 lôøi giaûi) c. d. g ( A, B, C , D ) = ∑ (4, 6, 9, 10, 11, 12, 13, 14) vôùi N = 2, 5, 7, 8 (3 lôøi giaûi) e. g (W , X , Y , Z ) = ∑ (0, 1, 4, 6, 10, 14) vôùi N=5, 7, 8, 9, 11, 12, 15(13 lôøi giaûi) 17. Toái thieåu caùc bieåu thöùc sau (laøm taát caû caùc tröôøng hôïp coù theå): a. f (W , X ,Y , Z ) = ∑ (2, 5, 7, 8, 10, 12, 13, 15 ) f ( A, B, C , D ) = ∑ (0, 4, 5, 6, 7, 8, 9, 10, 11, 13, 14, 15 ) b. f (W , X ,Y , Z ) = ∑ (1, 3, 5, 6, 7, 13, 14 ) vôùi N = 8, 10, 12 c. f ( A, B, C , D ) = ∑ (0, 3, 5, 6, 7, 9, 10, 11, 12, 13, 14 ) d. 18. Toái thieåu caùc bieåu thöùc sau (laøm taát caû caùc tröôøng hôïp coù theå): a. f ( A, B, C , D ) = ∑ (1, 2, 3, 5, 6, 7, 8, 11, 13, 14, 15 ) b. g (W , X ,Y , Z ) = ∑ (0, 2, 5, 7, 8, 10, 12, 13) c. h( A, B, C , D ) = ∑ (2, 4, 5, 6, 7, 8, 10, 12, 13, 15 ) f ( A, B, C , D ) = ∑ (1, 3, 4, 5, 6,11, 12, 13, 14, 15 ) d. Trang 3
  8. Baøi taäp Kyõ thuaät soá Chöông 4 19. Toái thieåu caùc bieåu thöùc sau (laøm taát caû caùc tröôøng hôïp coù theå): a. g (W , X ,Y , Z ) = ∑ (2, 3, 6, 7, 8, 10, 11, 12, 13, 15 ) b. h(P, Q , R, S ) = ∑ (0, 2, 3, 4, 5, 8, 11, 12, 13, 14, 15 ) f (W , X ,Y , Z ) = ∑ (0, 2, 3, 4, 5, 8, 10, 11, 12, 13, 14, 15) c. f (W , X ,Y , Z ) = ∑ (0, 1, 2, 4, 5, 6, 9, 10, 11, 13, 14, 15) d. 20. Toái thieåu caùc bieåu thöùc sau (laøm taát caû caùc tröôøng hôïp coù theå): a. g ( A, B, C , D ) = (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 15) ∑ h(W , X , Y , Z ) = ∑ (0, 2, 3, 5, 6, 7, 8, 10, 12, 13) b. f ( A, B, C , D ) = ∑ (0, 1, 2, 4, 5, 6, 7, 8, 9, 10, 11, 13, 14, 15) c. f ( A, B, C , D ) = ∑ (0, 3, 5, 6, 7, 9, 10, 11, 12, 13, 14 ) d. 21. Toái thieåu caùc bieåu thöùc sau (laøm taát caû caùc tröôøng hôïp coù theå): a. f (W , X , Y , Z ) = (1, 3, 6, 8, 11, 14) vôùi N = 2, 4, 5, 13, 15 ∑ f ( A, B, C , D ) = ∑ (0, 3, 6, 9, 11, 13, 14 ) vôùi N = 5, 7, 10, 12 b. f ( A, B, C , D ) = ∑ (0, 2, 3, 5, 7, 8, 9, 10, 11) vôùi N = 4, 15 c. f (W , X , Y , Z ) = ∑ (0, 2, 4, 5, 10, 12, 15) vôùi N = 8, 14 d. 22. Toái thieåu caùc bieåu thöùc sau (laøm taát caû caùc tröôøng hôïp coù theå): a. f ( A, B, C , D ) = (5, 7, 9, 11, 13, 14) vôùi N = 2, 6, 10, 12, 15 ∑ f ( A, B, C , D ) = ∑ (0, 2, 4, 5, 6, 7, 8, 9, 10, 14 ) vôùi N = 3, 13 b. f (W , X , Y , Z ) = ∑ (1, 2, 5, 10, 12 ) vôùi N = 0, 3, 4, 8, 13, 14, 15 c. f (W , X , Y , Z ) = ∑ (0, 4, 6, 9, 10, 11, 14 ) vôùi N = 1, 3, 5, 7 d. 23. Toái thieåu caùc bieåu thöùc sau (laøm taát caû caùc tröôøng hôïp coù theå): a. f ( A, B, C , D ) = (0, 1, 2, 5, 7, 9) vôùi N = 6, 8, 11, 13, 14, 15 ∑ f (W , X , Y , Z ) = ∑ (4, 6, 9, 10, 11, 13) vôùi N = 2, 12, 15 b. f ( A, B, C , D ) = ∑ (0, 1, 4, 6, 10, 14 ) vôùi N = 5, 7, 8, 9, 11, 12, 15 c. f (W , X , Y , Z ) = ∑ (1, 3, 7, 11, 13, 14 ) vôùi N = 0, 2, 5, 8, 10, 12, 15 d. 24. Toái thieåu caùc bieåu thöùc sau (laøm taát caû caùc tröôøng hôïp coù theå): a. f ( A, B, C , D, E ) = ∑ (0, 5, 7, 9, 11, 13, 15, 18, 19, 22, 23, 25, 27, 28, 29, 31) b. g ( A, B, C , D, E ) = ∑ (0, 2, 4, 7, 8, 10, 15, 17, 20, 21, 23, 25, 26, 27, 29, 31) c. g (V , W , X , Y , Z ) = ∑ (0, 1, 4, 5, 6, 7, 10, 11, 14, 15, 21, 24, 25, 26, 27 ) (3 lôøi giaûi) f (V , W , X , Y , Z ) = ∑ (0, 1, 5, 6, 7, 8, 9, 14, 17, 20, 21, 22, 23, 25, 28, 29, 30 ) d. (3 lôøi giaûi) e. h( A, B, C , D, E ) = ∑ (1, 3, 10, 14, 21, 26, 28, 30) vôùi N = 5, 12, 17, 29 Trang 4
  9. Baøi taäp Kyõ thuaät soá Chöông 4 25. Toái thieåu caùc bieåu thöùc sau (laøm taát caû caùc tröôøng hôïp coù theå): ⎛ 0, 1, 5, 7, 8, 9, 11, 13, 15, 18, 20, ⎞ f ( A, B, C , D, E ) = ∑ ⎜ ⎟ a. ⎜ 21, 23, 26, 28, 29, 31 ⎟ ⎝ ⎠ ⎛ 0, 1, 2, 4, 5, 6, 10, 13, 14, 18, 21, 22, ⎞ b. g ( A, B, C , D, E ) = ∑ ⎜ ⎟ ⎟ ⎜ 24, 26, 29, 30 ⎠ ⎝ c. h( A, B, C , D, E ) = ∑ (5, 8, 12, 13, 15, 17, 19, 21, 23, 24, 28, 31 ) ⎛ 2, 4, 5, 6, 10, 11, 12, 13, 14, 15, 16, 17, ⎞ f (V ,W , X ,Y , Z ) = ∑ ⎜ ⎟ d. ⎟ ⎜18, 21, 24, 25, 29, 30, 31 ⎠ ⎝ 26. Ñôn giaûn caùc bìa Karnaugh sau a) c) b) Trang 5
  10. Baøi taäp Kyõ thuaät soá Chöông 5 Baøi taäp chöông 5 1. Xaùc ñònh ngoõ ra cuûa RS-FF coù nhöõng ngoõ vaøo nhö sau 2. Xaùc ñònh ngoõ ra cuûa JK-FF coù nhöõng ngoõ vaøo nhö sau 3. Xaùc ñònh ngoõ ra cuûa D-FF coù nhöõng ngoõ vaøo nhö sau 1 Kyõ Thuaät Soá
  11. Baøi taäp Kyõ thuaät soá Chöông 5 4. Xaùc ñònh ngoõ ra cuûa maïch logic coù nhöõng ngoõ vaøo nhö sau 5. Cho maïch logic nhö hình veõ, xaùc ñònh taàn soá ngoõ ra cuûa maïch 6. Xaùc ñònh ngoõ ra cuûa maïch sau 2 Kyõ Thuaät Soá
  12. Baøi taäp Kyõ thuaät soá Chöông 5 7. Veõ daïng soùng ngoõ ra Q theo tín hieäu xung clock 3 Kyõ Thuaät Soá
  13. Baøi taäp Kyõ thuaät soá Chöông 7 Baøi taäp chöông 7 1. Sử dụng JK-FF để thiết kế bộ đếm không đồng bộ MOD-24. 2. Sử dụng IC 74LS293 để thiết lập bộ chia tần số từ 18Kpps xuống còn 1,2Kpps. 3. Sử dụng IC 74LS293 để thiết lập mạch chia 60. 4. Xác định tần số ngõ ra X 5. (a) Vẽ sơ đồ mạch đếm xuống không đồng bộ MOD-16. (b) Xác định sơ đồ trạng thái của bộ đếm (c) Nếu bộ đếm đang ở trạng thái 0110, xác định trạng thái của bộ đếm sau 37 chu kỳ xung clock. 6. Thiết kế bộ đếm đồng bộ cho chuỗi đếm sau: 000, 010, 101, 110 và lặp lại. Các trạng thái không xuất hiện (001, 011, 100 và 111) phải chuyển đến trạng thái 000 ở xung clock tiếp theo. 7. Thiết lập sơ đồ mạch bộ đếm đồng bộ MOD-64. 8. Thiết kế bộ đếm đồng bộ MOD-12 sử dụng cổng NAND và a. RS-FF b. JK-FF c. D-FF 9. Thiết kế một dãy tín hiệu tuần hoàn dùng JK-FF và mạch NAND như bảng sau Xung lock C B A 1 0 0 1 2 1 0 0 3 0 1 0 4 1 0 1 5 1 1 0 6 0 1 1 Vẽ dạng tín hiệu của A, B, C. 10. Xây dựng bộ đếm vòng với MOD-6 dùng Flip Flop loại D. 11. Xây dựng bộ đếm vòng với MOD-8 dùng Flip Flop loại RS. 12. Thieát keá maïch daõy tín hieäu tuaàn hoaøn nhö sau, duøng RS-FF. 000 101 010 110 011 001 1
  14. Baøi taäp Kyõ thuaät soá Chöông 7 13. Thieát keá maïch daõy tín hieäu tuaàn hoaøn nhö sau, duøng JK-FF. 100 111 000 101 001 110 010 011 14. Thiết kế mạch đếm đồng bộ modulo-12 dùng FF JK. Dùng ngã ra mạch đếm để điều khiển hệ thống đèn giao thông: - Đèn xanh cháy trong 40 s - Đèn vàng cháy trong 20s - Đèn đỏ cháy trong 40s - Đèn vàng và đỏ cùng cháy trong 20s. Chu kỳ lặp lại Cho chu kỳ xung đồng hồ là 10s. 15. Thiết kế mạch đếm đồng bộ dùng FF JK có ngã vào điều khiển X: - Khi X=0 mạch đếm theo thứ tự 0, 2, 4, 6 rồi trở về 0 - Khi X=1 mạch đếm 0, 6, 4, 2 rồi trở về 0. Các trạng thái không sử dụng trong hai lần đếm đều trở về 0 khi có xung đồng hồ 2
  15. Baøi taäp Kyõ thuaät soá Chöông 9 Baøi taäp chöông 9 1. Xaùc ñònh giaù trò caùc ngoõ ra vôùi caùc giaù trò ngoõ vaøo nhö sau: a. Taát caû caùc ngoõ vaøo ôû möùc thaáp. b. Taát caû caùc ngoõ vaøo ôû möùc thaáp ngoaïi tröø E3 = 1. c. Taát caû caùc ngoõ vaøo ôû möùc cao ngoaïi tröø E1 = E 2 = 0 d. Taát caû caùc ngoõ vaøo ôû möùc cao. 2. Xaùc ñònh caùc ñieàu kieän ñeå O6 cuûa IC 74LS138 ôû möùc thaáp. 3. Söû duïng IC 74LS138 ñeå thieát keá boä giaûi maõ 4 sang 16 (boä giaûi maõ 1-16). 4. Söû duïng IC 74LS138 ñeå thieát keá boä giaûi maõ 5 sang 32 (boä giaûi maõ 1-32). 5. Duøng moät maïch giaûi maõ töø 3 sang 8 ñöôøng vaø caùc coång logic caàn thieát ñeå thöïc hieän caùc haøm sau a. F1 = ∑ (1, 2, 3) b. F1 = ∑ (4, 5, 7 ) c. F1 = ∑ (1, 2, 3, 4, 5, 7 ) 6. Xaùc ñònh ngoõ ra cuûa IC 74LS174 khi A8 = A4 = 0 vaø taát caû caùc ngoõ vaøo coøn laïi ñeàu ôû möùc cao. 1
  16. Baøi taäp Kyõ thuaät soá Chöông 9 7. Giaûi thích hoaït ñoäng cuûa maïch ôû hình sau. Maïch naøy duøng ñeå laøm gì? 8. Söû duïng IC 74LS85 ñeå thieát keá boä so saùnh 6 bit. 9. Söû duïng IC 74LS85 ñeå thieát keá boä so saùnh 10 bit. 10. Söû duïng IC 74LS155 ñeå thieát keá boä giaûi maõ töø 3 sang 8. 11. Söû duïng IC 74LS155 ñeå thieát keá boä taùch keânh 1 sang 8. 12. Xaùc ñònh chöùc naêng hoaït ñoäng cuûa maïch logic sau. 13. Söû duïng IC 74LS42 ñeå thieát keá boä taùch keânh 1 sang 8. 14. Söû duïng IC 74151 ñeå taïo ra moät maïch logic Z = AB + BC + AC 2
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

LV.15: Bộ Đồ Án Tốt Nghiệp Chuyên Ngành Cơ Khí
65 tài liệu
2431 lượt tải
THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
2=>2