StuDocu is not sponsored or endorsed by any college or university
Nhóm07-Áp dụng thuật giải heuristic cho bài toán tô màu tối
ưu trên đồ thị
Công nghệ phần mềm (Trường Đại Học Điện Lực)
StuDocu is not sponsored or endorsed by any college or university
Nhóm07-Áp dụng thuật giải heuristic cho bài toán tô màu tối
ưu trên đồ thị
Công nghệ phần mềm (Trường Đại Học Điện Lực)
Downloaded by Dung Nguyen (tridanh2468@gmail.com)
lOMoARcPSD|16911810
TRƯỜNG ĐẠI HỌC ĐIỆN LỰC
KHOA CÔNG NGHỆ THÔNG TIN
BÁO CÁO CHUYÊN ĐỀ HỌC PHẦN
NHẬP MÔN TRÍ TUỆ NHÂN TẠO
ĐỀ TI:
Áp dụng thuật giải heuristic cho bài toán tô màu tối ưu trên đồ thị
Sinh viên thực hiện : PHẠM VĂN TUẤN
NGUYỄN HONG HIỆU
NGUYỄN DỨC THUẬN
Giảng viên hướng dẫn : VŨ VĂN ĐỊNH
Ngành : CÔNG NGHỆ THÔNG TIN
Chuyên ngành : HỆ THỐNG THƯƠNG MẠI ĐIỆN
TỬ
Lớp : D14HTTMDT1
Khóa : 2019
Hà Nội, tháng 10 năm 2021
Phiếu chấm điểm
Downloaded by Dung Nguyen (tridanh2468@gmail.com)
lOMoARcPSD|16911810
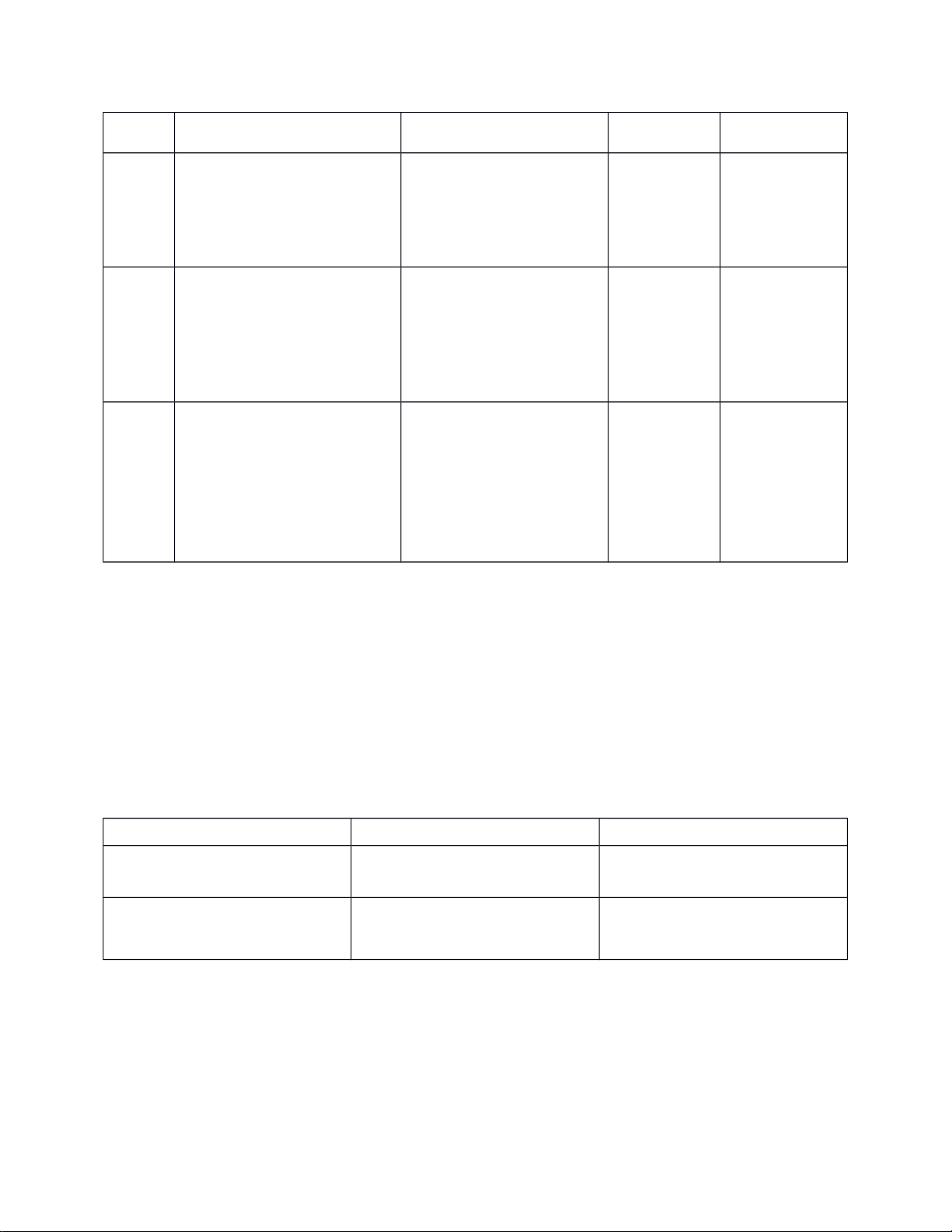
STT Họ tên sinh viên Nội dung thực hiện Điểm Chữ ký
1 Phạm Văn Tuấn Làm báo cáo
Làm chương trình
2 Nguyễn Hoàng Hiệu Làm báo cáo
Làm chương trình
3 Nguyễn Đức Thuận Làm báo cáo
Làm chương trình
Họ tên giảng viên Chữ ký Ghi chú
Downloaded by Dung Nguyen (tridanh2468@gmail.com)
lOMoARcPSD|16911810
M C L CỤ Ụ
I. GIỚI THIỆU BI TOÁN..................................................................................................................4
1. Tổng quan về heuristic..................................................................................................................4
1.1. Heuristic và các cách biểu diễn đồ thị.......................................................................................4
1.2. Các bài toán điển hình................................................................................................................6
2. Bài toán tô mầu đồ thị...................................................................................................................6
2.1. Bài toán tô mầu cạnh..................................................................................................................6
2.2. Bài toán tô mầu đỉnh..................................................................................................................6
2.3. Các khái niệm liên quan.............................................................................................................7
2.4. ng d ngỨ ụ ......................................................................................................................................8
II. GIẢI THUẬT.................................................................................................................................9
1. Bài toán tô mầu đỉnh.....................................................................................................................9
1.1. Các định nghĩa sử dụng:........................................................................................................9
1.2. Thuật toán............................................................................................................................10
1.3. Ví dụ......................................................................................................................................12
2. Bài toán tô mầu cạnh...................................................................................................................17
2.1. Giải thuật..............................................................................................................................17
2.3. Độ phức tạp:.........................................................................................................................23
III. CI ĐẶT THUẬT TOÁN...........................................................................................................24
1. Bài toán tô mầu đỉnh.......................................................................................................................24
2. Bài toán tô mầu cạnh.......................................................................................................................30
2.1. Đ c d li u t fleọ ữ ệ ừ ..................................................................................................................30
2.2. D li u vào t bàn phímữ ệ ừ ........................................................................................................40
3. Mã nguồn......................................................................................................................................51
IV. TI LIỆU THAM KHẢO...........................................................................................................52
PHỤ LỤC 1: DANH MỤC CÁC HÌNH ẢNH TRONG TI LIỆU...................................................53
PHỤ LỤC 2: PHÂN CHIA CÔNG VIỆC..............................................................................................53
Downloaded by Dung Nguyen (tridanh2468@gmail.com)
lOMoARcPSD|16911810
I. GIỚI THIỆU BI TOÁN
1. Thuật giải heuristic
1.1.khái niệm heuristic
Là mở rộng khái niệm thuật toán.
oThuờng tìm lời giải tốt nhưng không tốt nhất.
oNhanh chóng tìm ra kết quả hơn so với giải thuật tối ưu, vì vậy chi phí thấp hơn.
oThuờng thể hiện khá tự nhiên, gần gũi với cách suy nghĩ và hành động của con
nguời.
Các nguyên lý của thuật giải heuristic
Vét c n thông minhạ
Nguyên lý th tứ ự
Nguyên lý tham lam
Hàm heuristic
Kyỹ thu t heuristic:ậ
Theo T đi n tiêếng Anh Oxford: “Heuristics là ngh thu t tm kiêếm chân lý. Nói riêng, ừ ể ệ ậ
heuristics là đ c tr ng c a quá trình h c nh đó các h c sinh h c đ c cách t tm ra cách ặ ư ủ ọ ờ ọ ọ ượ ự
gi i thíchả các hi n t ng t nhiên”.ệ ượ ự
T “Heuristics” có cùng m t gôếc tiêếng Hy L p nh t Eureka. Feigenbaum Feldman đã ừ ộ ạ ư ừ
đ a ra đ nh nghĩa :ư ị
“Heuristics (Các quy tắếc heuristics, các ph ng pháp heuristics) là các quy tắếc, ph ng ươ ươ
pháp, chiêến l c, m o gi i hay ph ng cách nào đó nhắằm làm gi m khôếi l ng tm kiêếm l i ượ ẹ ả ươ ả ượ ờ
gi i trong không gian bài tóan c c l n”.ả ự ớ
2. Bài toán tô mầu đồ thị
Tô màu đồ thị và sự tổng quát của nó là công cụ hữu dụng trong việc mô hình hóa rất nhiều bài
toán khác nhau trong vấn đề xếp lịch, xây dựng chương trình và vấn đề phân công công việc. Bài
toán tô màu đồ thị bao gồm nhiều loại: tô màu đỉnh đồ thị (vertex graph coloring) , tô màu cạnh
đồ thị (edge graph coloring) ...
2.1. Bài toán tô mầu cạnh
Bài toán
Cho G=(V,E) là đơn đồ thị vô hướng ( G không là đồ thị khuyên) , hãy tìm cách gán (tô màu) cho
mỗi cạnh của đồ thị một màu sao cho hai cạnh có cùng chung 1 đỉnh không bị tô bởi cùng một
màu. Một phép gán màu cho các cạnh như vậy gọi là một phép tô màu cạnh đồ thị. Nói cách
khác, phép tô cạnh đồ thị bởi k màu nói trên có thể được hiểu là một phân hoạch của tập cạnh E
của G thành k tập con (tương ứng với k màu) sao cho mỗi tập con ứng với một màu i nhất định.
Bài toán đặt ra là tìm cách tô màu nào sử dụng số màu ít nhất có thể.
Ví dụ
Downloaded by Dung Nguyen (tridanh2468@gmail.com)
lOMoARcPSD|16911810