
NGHIÊN CỨU HIỆN TƯỢNG CỘNG HƯỞNG PHI TUYẾN
TRONG THIẾT BỊ ĐIỆN CHỨA CUỘN DÂY LÕI THÉP
BẰNG PHƯƠNG PHÁP MÔ PHỎNG
TS. LÊ MẠNH VIỆT
Bộ môn Trang bị điện
Khoa Điện – Điện tử
Trường Đại học Giao thông Vận tải
Tóm tắt: Cuộn dây lõi thép làm việc ở điểm gần bão hoà sẽ cộng hưởng nếu nó được nối
thêm 1 tụ điện và kích thích điều hoà với biên độ đủ lớn. Cộng hưởng phi tuyến có những đặc
tính rất đa dạng phụ thuộc vào các thông số điện từ của mạch, nhất là trạng thái bão hoà của
lõi thép. Mô phỏng mạch điện khi cộng hưởng phi tuyến đóng vai trò quan trọng trong phân
tích, vận hành, sửa chữa và định hướng thiết kế thiết bị điện.
Bài báo này trình bày kết quả nghiên cứu việc mô phỏng biên độ từ thông là nghiệm của
phương trình vi phân phi tuyến khi cộng hưởng. Chương trình mô phỏng này viết bằng ngôn
ngữ C với nhiều đồ thị sẽ rất hiệu quả cho việc phân tích đánh giá thiết bị điện ấy. Hơn thế
nữa phương pháp thành lập, phân tích cũng như chương trình mô phỏng là rất bổ ích cho các
kỹ sư, giảng viên, sinh viên ngành điện điện tử trong chuyên môn của mình.
Summary: The iron core inductor operating in the proximity of saturation point will
resonate if this inductor connects to a capacitor and harmonizes excitement with sufficent
amplitude. Non-linear resonance possesses various characteristics dependent on the circuit ‘s
electromechanical parameters, especially state of saturation of the iron core. Simulating
electrical circuits which are non-linear resonance plays an important role in analysing,
operating, reparing and orienting towards design of electric equipment.
This paper introduces research results in simulating the magnetic flux‘s amplitudes
which are roots of non-linear differential equation in resonant state. This simulation program
using C programming language with many graphs effectively assists to analyse and evaluate
the equipment. Furthermore, the methods of foundation, and analysis as well as simulation
program are useful tools for engineers, lecturers and students of Electronic Electrical
Engineering.
ĐT
I. ĐẶT VẤN ĐỀ
Cộng hưởng trong mạch tuyến tính (thông số của các phần tử là hằng) xảy ra khi tần số
nguồn kích thích bằng tần số riêng của mạch. Tại tần số cộng hưởng chứa nhiều thông tin, như:
dòng hoặc áp cực đại (do kết cấu mạch quyết định), công suất nhỏ nhất hay lớn nhất, thành phần
dòng hay áp trên cuộn cảm và tụ điện bằng nhau về trị số… Trong mạch phi tuyến (khi chính
xác) khái niệm cộng hưởng có nhiều điểm khác hẳn so với mạch tuyến tính. Nói đúng ra cần
định nghĩa cộng hưởng theo đặc trưng khác, tổng quát hơn và vì thế có cách nhìn nhận, phân
tích mạch điện hiệu quả hơn. Để phân tích mạch điện phi tuyến ở trạng thái đã xác lập có nhiều
phương pháp, song đều là gần đúng. Hơn thế nữa lúc chọn phương pháp sử dụng đã nhắm đến
hoặc tiên lượng tới khả năng nghiệm của bài toán, đấy cũng chính là ưu điểm và hạn chế của các
phương pháp trước đây. Ưu điểm vì mục đích của thiết bị điện cụ thể cần nghiệm bài toán phi
tuyến như thế nào để nó thực hiện được chức năng thiết kế đề ra. Còn sự hạn chế phụ thuộc vào
phương pháp gần đúng do trình độ khoa học của mình và mức độ công nghệ của thiết bị, máy
móc lúc thiết kế.
Trong trường hợp xem xét thiết bị điện từ chứa cuộn dây lõi thép bão hoà phục vụ trong
các hệ thống máy điện, khí cụ điện, chính chúng ta phải tiên lượng nghiệm của các bài toán trên.
Do thiết bị điện từ làm việc được trong hệ thống lưới điện công nghiệp thì nghiệm của các bài
toán bắt buộc chứa tần số công nghiệp hay tần số cơ bản, dù đáp ứng của hệ thống có chứa
nhiều tần số cao khác. Với mục tiêu giảm thiểu biên độ các sóng hài bậc cao cho các thiết bị
điện từ, nên việc giả thiết nghiệm có chứa và nên chứa số lượng chính tần số cơ bản sẽ là tiền
đề, nền tảng cho việc phân tích cộng hưởng phi tuyến gắn với mục đích hoạt động của thiết bị.
II. NỘI DUNG
1. Bài toán phi tuyến với thiết bị điện từ chứa cuộn dây lõi thép
Cuộn dây lõi thép trong thiết bị điện từ ở trạng thái bắt đầu bão hoà và bão hoà có đặc tính
dòng điện - từ thông dạng:
ĐT
iL(j) = a1 Ψ+ a3Ψ3 (1)
trong đó: a1, a3 là các hằng số.
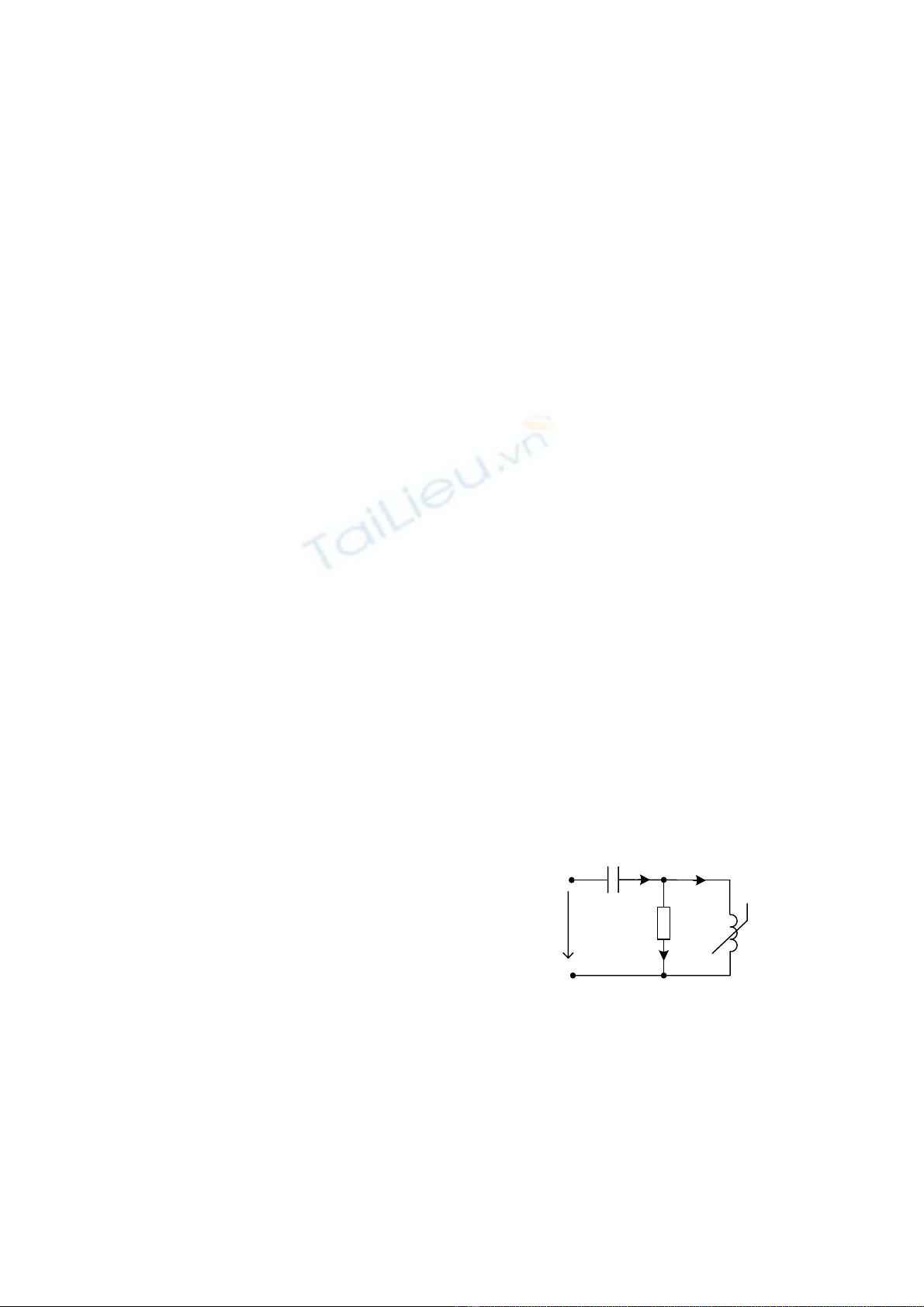
Một thiết bị điện từ đơn giản nhất và cũng phổ thông nhất có dạng mạch điện tương đương
hình 1, trong đó ngoài 2 phần tử tuyến tính R, C thì cuộn dây lõi thép phi tuyến có dạng công
thức (1).
Khi làm việc với lưới điện công nghiệp, nguồn
kích thích là nguồn áp điều hoà :
Hình 1. Mạch điện tương đương
của thiết bị điện từ chứa cuộn dây
lõi thép nối với tụ điện:
u~(t) = E m.sin(ωt + θ) (2)
trong đó biên độ E m có thể thay đổi trong những
điều kiện làm việc nào đó (nhất là lúc sự cố). Phương
trình Kiếchốp K1 cho nút:
iC = iL + ig = iL + g.uL (3a)
trong đó g = 1/R là điện dẫn, và dòng qua tụ điện :
iC = C. (duC /dt) (3b)

Phương trình Kiếchốp K2 cho vòng:
u~ = uL + uC (4)
trong đó có: uL = dψ/dt (5)
Đưa (5), (4) vào (3), sau đó đạo hàm 2 vế sẽ được phương trình:
dt
du
C
i
dt
d
.
C
g
dt
d~L
2
2
=+
Ψ
+ (6a)
Ψ’’+ (g/C)Ψ’+(1/C) iL= u’~ (6b)
Thay (1) iL = a1ψ + a3ψ3 vào (6b) sẽ được:
ψ’’ + kψ’ + αψ + βψ3 = u’~ (7a)
trong đó: k = g/C, α = a1/C và β = a3/C
(7b)
Chúng ta có thể chứng minh được dạng thiết bị điện từ có sơ đồ tương đương chỉ toàn nối
tiếp R - C và cuộn dây lõi thép cũng có dạng phương trình (7a), nhưng với các hệ số khác.
Phương trình vi phân trên sẽ có nghiệm xác lập khi giả thiết các điều kiện đầu bằng không, hoặc
sau một thời gian đủ lớn các thành phần tự do đã triệt tiêu.
Tần số riêng của hệ thống tuyến tính suy biến (β = 0) tìm được từ phương trình đồng nhất
(u~ = 0) và không tiêu tán (k = 0):
Ψ’’+ αΨ =0 (8) ĐT
trong đó tần số riêng ω2 = α = a1/C (9)
Hệ thống trở thành tuyến tinh khi thành phần phi tuyến bậc 3 với β = 0:
Ψ’’+ αΨ + k.Ψ’ = u’~ (10)
Trong đó tiêu tán (hoặc là công suất thiết bị tiêu thụ) trong hệ thống thể hiện bằng hệ số
k = g/C.
Như đã phân tích chúng ta cần và bắt buộc thiết bị điện từ đang xem xét phải chứa tần số
công nghiệp là chính, và cần có nghiệm thoả mãn nhất định bài toán đề ra. Trên cơ sở ấy giả
thiết nghiệm xác lập của từ thông (thông số đặc trưng nhất cho cuộn dây) chứa tần số cơ bản khi
đã bỏ các điều hoà bậc cao:
Ψ = Acos ωt (11)
Sau đây tính các đạo hàm để thế vào phương trình (7a),
ψ’ = - ωAsinωt, (12)
ψ’’ = - ω2 A cosωt, (13)
Đạo hàm u~(t) trong (2), sau đó ký hiệu:
u’~ = F. cos (ωt + θ), (14a)
u’~ = G cos ωt – H sinωt, (14b)
trong đó: F = ωEm, G = Fcosθ, H = Fsinθ, tgθ = H/G (15)
Thay các kết quả từ (11) tới (15) vào phương trình (7a), sau đó dùng phương pháp cân
bằng điều hòa bỏ qua tần số bậc cao sẽ nhận được hệ phương trình đại số :
(α - ω2). A + (3/4). β. A3= G (16)
A.k.ω = H (17)
G2 + H2 = F2 (18)
[(α-ω2).A+(3/4).β.A3]2 + A2.k2.ω2 = F2 (19)
Để giải (16,17 và 18 hay 19) tìm nghiệm A với các giá trị α, β, k và F cụ thể sẽ không khó
khăn gì, nhưng chỉ được 1 giá trị không có ý nghĩa tổng quát.
2. Sử dụng phương pháp mô phỏng phân tích thiết bị điện chứa cuộn dây lõi thép bão
hoà nối với tụ điện
Phương trình (7a) có nghiệm là từ thông ψ(t) của thiết bị điện từ điển hình và nghiệm này
gần đúng chỉ chứa tần số cơ bản. Nhưng biên độ từ thông A phụ thuộc vào tần số theo cách nào,
cũng như phụ thuộc các thông số khác hay không và nó có những tính chất , đặc điểm gì... Dựa
vào khái niệm về cộng hưởng đã phân tích, ở đây coi rằng biên độ từ thông A(ω) phụ thuộc vào
tần số ω. Để giải tổng quát (7a) ta mô phỏng nghiệm A(ω) theo phưong trình (19). A(ω) được
xây dựng bằng các đồ thị theo các giá trị của thông số các phần tử tuyến tính, phi tuyến cùng
biên độ kích thích.
ĐT 3. Kết quả các đồ thị mô phỏng ( xem các đồ thị )
Để xem xét đủ các trường hợp, khả năng mà thiết bị điện từ cuộn dây lõi thép nối với tụ
điện có thể gặp, ta phân loại chúng như sau:
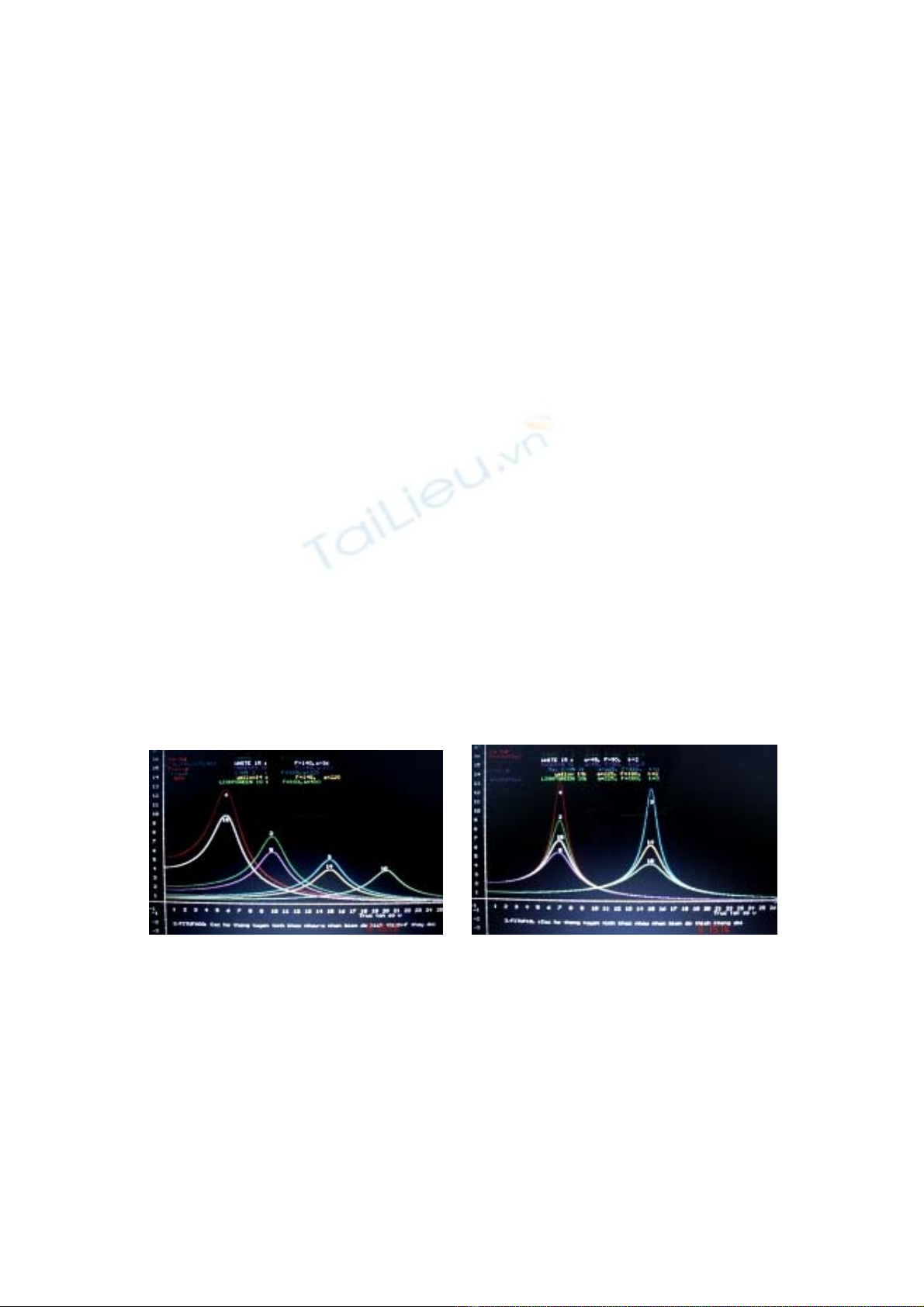
Hình 2. Tuyến tính k hằng Hình 3. Tuyến tính tổn hao k khác nhau
+ Lõi thép làm việc trong vùng chưa bão hoà hay là thiết bị điện từ ở chế độ tuyến tính, hệ
số bậc 3 trong công thức (1) có β = 0. Lúc này nhận được 2 đồ thị.
Hình 2 có bốn dạng đồ thị khi chung giá trị k = 2,5 gồm:
+ α = 36(F = 180,140), + α = 100(F = 180,140),
+ α = 225(F = 180,140) và + α = 400(F = 180).
Hình 3 với hai dạng đồ thị gồm :

+ α = 49, F = 90 (k = 1; 1.5; 2; 2.5) và + α = 225, F = 180 (k = 1; 2; 3).
Hình 4. Fi tuyến tần số riêng β khác nhau Hình 5. Mức độ fi tuyến k khác nhau.
Hình 4 có F = 180, α = 45, K = 2 và β = invar(0; 0.5; 1; 1.5; 2; 2.5; 3).
Hình 5 có β = 3, α = 45, K = 2 và F = invar(400; 350; 300; 250; 200; 150; 100).
ĐT
Hình 6. Fi tuyến có tổn hao k thay đổi Hình 7. Fi tuyến α khác nhau
Hình 6 có F = 200, α = 45, β = 3 và K = invar(0.5; 1; 1.5; 2; 2.5; 3; 3.5).
Hình7 có F = 180, K = 2, β = 3 và α = invar(5; 45; 85; 125; 165; 205; 245).
+ Lõi thép làm việc trong vùng đã bão hoà ở mức độ khác nhau có β ≠ 0 với độ lớn khác
nhau. Chú ý rằng lõi thép thật thì trong công thức (1) có giá trị β > 0. Trường hợp này nhận
được đồ thị hình 4, hình 5, hình 6 và hình 7.
Hình 8. Tổng quát fi tuyến k hằng Hình 9. Tổng quát fi tuyến α hằng
Hình 8 có năm dạng đồ thị với thông số chung F = 220, k = 2:





![Giáo trình Phương pháp nghiên cứu khoa học Trường ĐH Nha Trang [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2023/20230131/baphap06/135x160/4821675131161.jpg)

![Giáo trình Phương pháp nghiên cứu khoa học: Phần 1 [FULL]](https://cdn.tailieu.vn/images/document/thumbnail/2023/20230111/phuong3659/135x160/1068230845.jpg)

















