Báo cáo thí nghi m h th ng đi u khi n sệ ệ ố ề ể ố
BÁO CÁO THÍ NGHI M H TH NG ĐI U KHI N SỆ Ệ Ố Ề Ể Ố
Sinh viên: Nguy n Th Đ cễ ế ứ
SHSV:20090812
L p: Đi u khi n & t đ ng hóa –K54ớ ề ể ự ộ
Bài s d ng: ử ụ và
I.M c đích bài th c hành.ụ ự
Giúp sinh viên làm quen v i công c và môi tr ng mô ph ngớ ụ ườ ỏ
Matlab/Simulink trong vi c mô hình hóa, phân tích và thi t k h th ng đi uệ ế ế ệ ố ề
khi n s (tài li u [1], vi t t t: ĐKS), qua đó n m v ng đ c các ki n th c cể ố ệ ế ắ ắ ữ ượ ế ứ ơ
b n nh :ả ư
•Các ph ng pháp gián đo n hóa h th ng đ i t ng đi u khi n (vi t t t:ươ ạ ệ ố ố ượ ề ể ế ắ
ĐTĐK)
•Ph ng pháp phân tích h th ng ĐKSươ ệ ố
•Thi t k th nghi m thu t toán ĐKSế ế ử ệ ậ
II. Nhi m v bài th c hành.ệ ụ ự
Bài t p th c hành đ c th c hi n d a trên các ki n th c đã đ c h c trênậ ự ượ ự ệ ự ế ứ ượ ọ
l p áp d ng cho m c đích phát tri n và thi t k vòng đi u ch nh cho h th ngớ ụ ụ ể ế ế ề ỉ ệ ố
đi u khi n đ ng c đi n m t chi u kích thích đ c l p (vi t t t: ĐCMC). Theoề ể ộ ơ ệ ộ ề ộ ậ ế ắ
[2], đ i t ng đi u khi n ĐCMC đ c mô t b i các ph ng trình d i đây:ố ượ ề ể ượ ả ở ươ ướ
−Đi n áp ph n ng:ệ ầ ứ = +
−S c đi n đ ng c m ng :ứ ệ ộ ả ứ
−T c đ quay :ố ộ
−Mô men quay :
−H ng s đ ng c : ằ ố ộ ơ
−H ng s th i gian ph n ng: ằ ố ờ ầ ứ
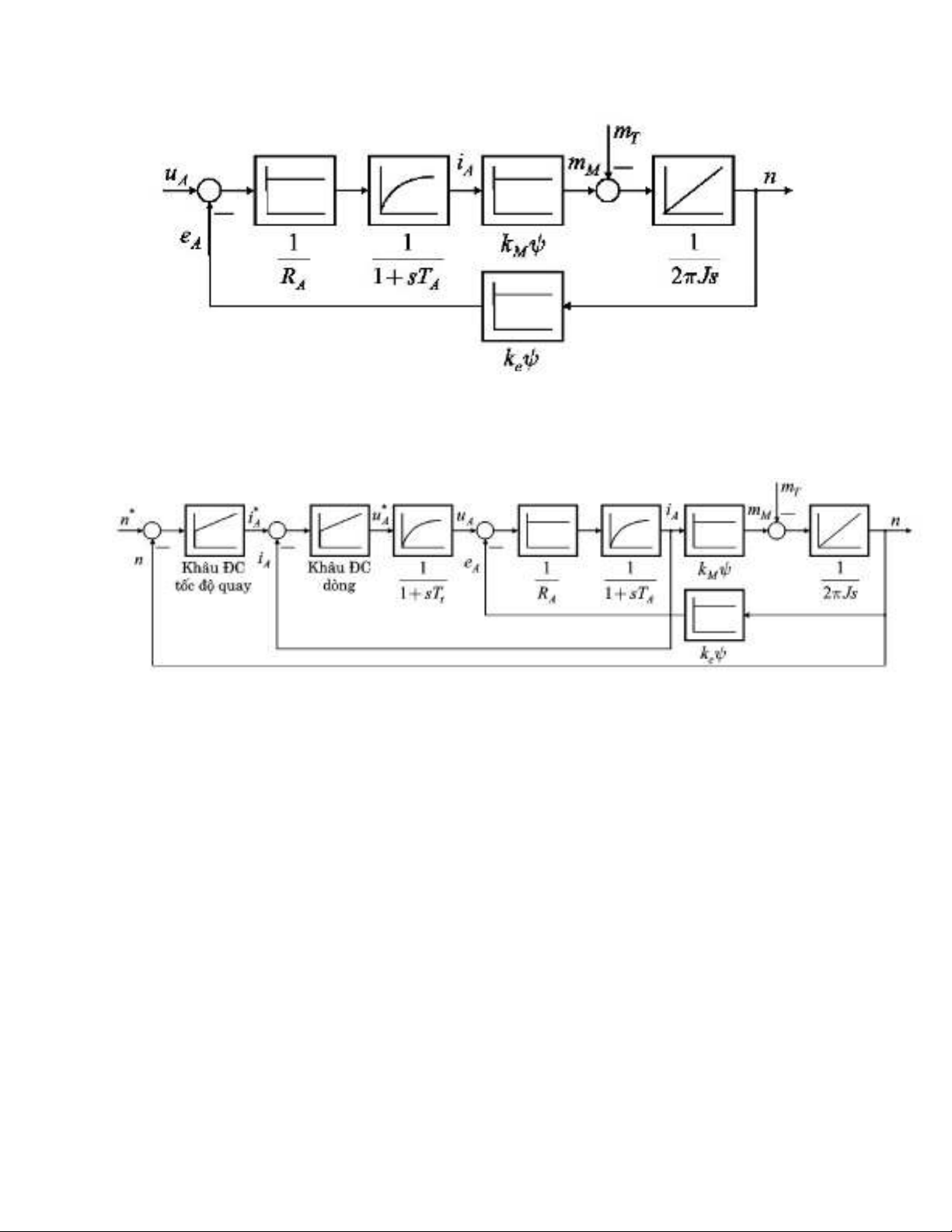
S đ c u trúc c a ĐCMC đ c minh h a hình v H.1 (tài li u [2], hình 9.1).ơ ồ ấ ủ ượ ọ ở ẽ ệ
Đ ng c có các tham s sau đây:ộ ơ ố
- Đi n tr ph n ng: RA = 250mΩệ ở ầ ứ
- Mô men quán tính: J = 0,012kgm2
- Đi n c m ph n ng: LA = 4mHệ ả ầ ứ
- H ng s đ ng c : ke = 236,8, kM = 38,2ằ ố ộ ơ
- T thông danh đ nh: ψR=0,04VSừ ị
Nguy n Th Đ c-20090812ễ ế ứ
ĐK&TĐH4-K54
Báo cáo thí nghi m h th ng đi u khi n sệ ệ ố ề ể ố
H. 1: S đ c u trúc c a ĐCMC kích thích đ c l pơ ồ ấ ủ ộ ậ
N i dung c a 4 bài th c hành nh m t o cho sinh viên kh năng thi t k hộ ủ ự ằ ạ ả ế ế ệ
th ng đi u khi n ĐCMC theo c u trúc Cascade nh hình (tài li u [2], hình 9.14)ố ề ể ấ ư ệ
sau đây:
H. 2: S đ h th ng đi u khi n ĐCMC theo c u trúc Cascadeơ ồ ệ ố ề ể ấ
Ngoài ra, sinh viên c n n m v ng ph ng pháp tìm mô hình gián đo n trênầ ắ ữ ươ ạ
không gian tr ng thái đ sau này có th thi t k h th ng đi u khi n ĐCMCạ ể ể ế ế ệ ố ề ể
trên không gian tr ng thái.ạ
III.K T QU TH C NGHI MẾ Ả Ự Ệ
Bài th c hành s 1: Tìm mô hình gián đo n c a ĐCMC.ự ố ạ ủ
1. S d ng ph ng pháp đã h c (m c 1.3.2b, tài li u [1]) đ xác đ nh hàmử ụ ươ ọ ụ ệ ể ị
truy n đ t trên mi n nh z thích h p đ thi t k vòng trong cùng ĐKề ạ ề ả ợ ể ế ế
dòng ph n ng (tài li u [2], hình 9.10). Chu kỳ trích m u đ c ch n là ầ ứ ệ ẫ ượ ọ TI
= 0,1ms và 0,01ms.
Hàm truy n h c a đ i t ng ĐCMC là:ề ở ủ ố ượ
Hàm truy n kín mô hình đ i t ng là:ề ố ượ
2.Th c hi n t i c a s Matlab command:ự ệ ạ ử ổ
Nguy n Th Đ c-20090812ễ ế ứ
ĐK&TĐH4-K54
Báo cáo thí nghi m h th ng đi u khi n sệ ệ ố ề ể ố
>> Ra=0.25; La=0.04; Ta=La/Ra; Ke=236.8; Km=38.2;
J=0.012; phi=0.04;
>> Wh=(1/Ra)*tf([1],[Ta 1])*Km*phi*tf([1],[2*pi*J 0])
Transfer function:
6.112
----------------------
0.01206 s^2 + 0.0754 s
>> Wk=feedback(Wh,Ke*phi)
Transfer function:
6.112
------------------------------
0.01206 s^2 + 0.0754 s + 57.89
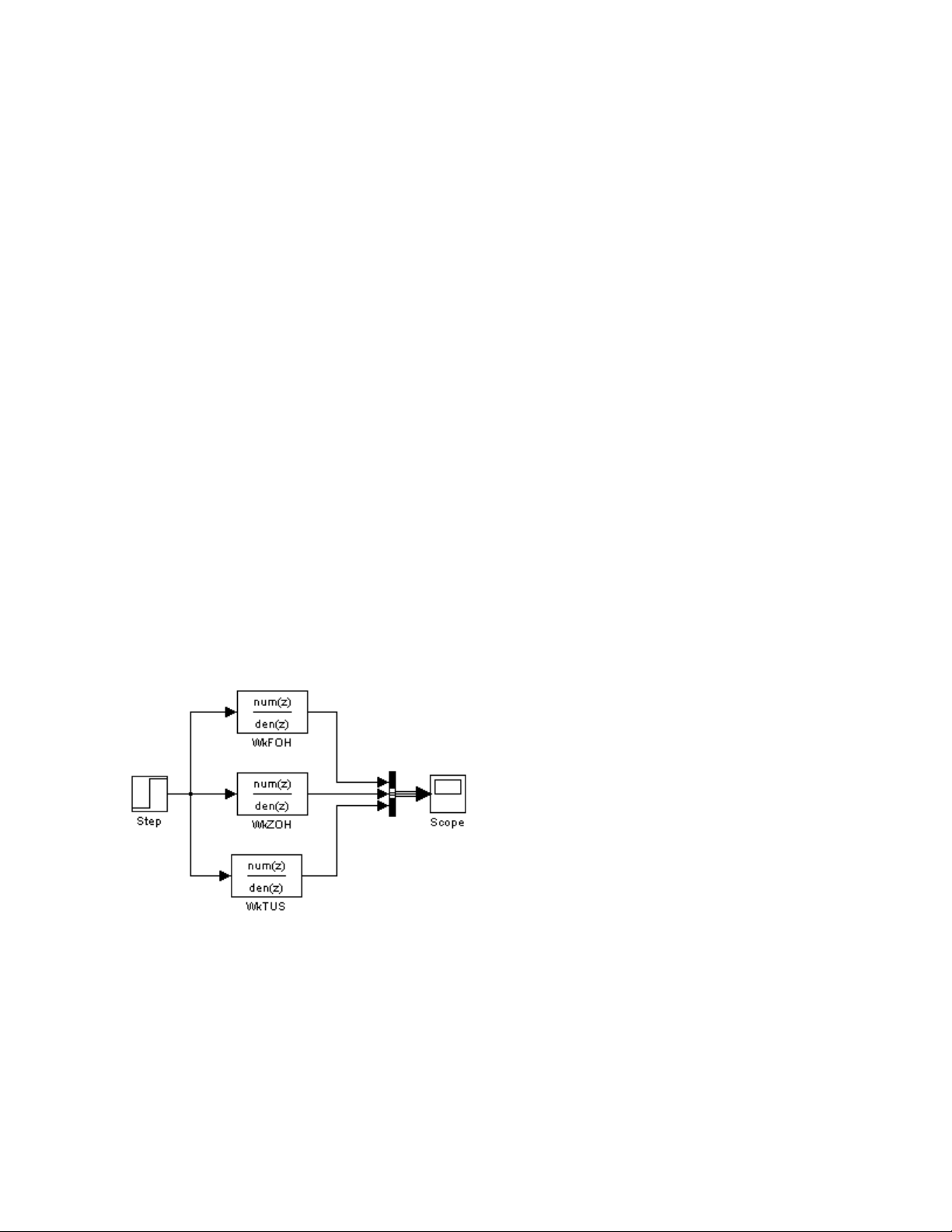
Đ tìm hàm truy n gián đo n c a đ i t ng ta s d ng l nh:ể ề ạ ủ ố ượ ử ụ ệ
>>c2d(sys,T,’method’)
>> Wkz1=c2d(Wk,0.1*10^-3,'ZOH')
Transfer function:
2.533e-006 z + 2.532e-006
-------------------------
z^2 - 1.999 z + 0.9994
Sampling time: 0.0001
>> Wkz2=c2d(Wk,0.1*10^-3,'FOH')
Transfer function:
8.443e-007 z^2 + 3.377e-006 z + 8.44e-007
-----------------------------------------
z^2 - 1.999 z + 0.9994
Sampling time:
0.0001
>> Wkz3=c2d(Wk,0.1*10^-3,'TUSTIN')
Transfer function:
1.266e-006 z^2 + 2.532e-006 z + 1.266e-006
------------------------------------------
z^2 - 1.999 z + 0.9994
Sampling time: 0.0001
Nguy n Th Đ c-20090812ễ ế ứ
ĐK&TĐH4-K54
Báo cáo thí nghi m h th ng đi u khi n sệ ệ ố ề ể ố
>> Wkz4=c2d(Wk,0.01*10^-3,'ZOH')
Transfer function:
2.533e-008 z + 2.533e-008
-------------------------
z^2 - 2 z + 0.9999
Sampling time: 1e-005
>> Wkz5=c2d(Wk,0.01*10^-3,'FOH')
Transfer function:
8.444e-009 z^2 + 3.378e-008 z + 8.444e-009
------------------------------------------
z^2 - 2 z + 0.9999
Sampling time: 1e-005
>> Wkz6=c2d(Wk,0.01*10^-3,'TUSTIN')
Transfer function:
1.267e-008 z^2 + 2.533e-008 z + 1.267e-008
------------------------------------------
z^2 - 2 z + 0.9999
Sampling time: 1e-005
3.Mô ph ng simulinkỏ
Nguy n Th Đ c-20090812ễ ế ứ
ĐK&TĐH4-K54
Báo cáo thí nghi m h th ng đi u khi n sệ ệ ố ề ể ố
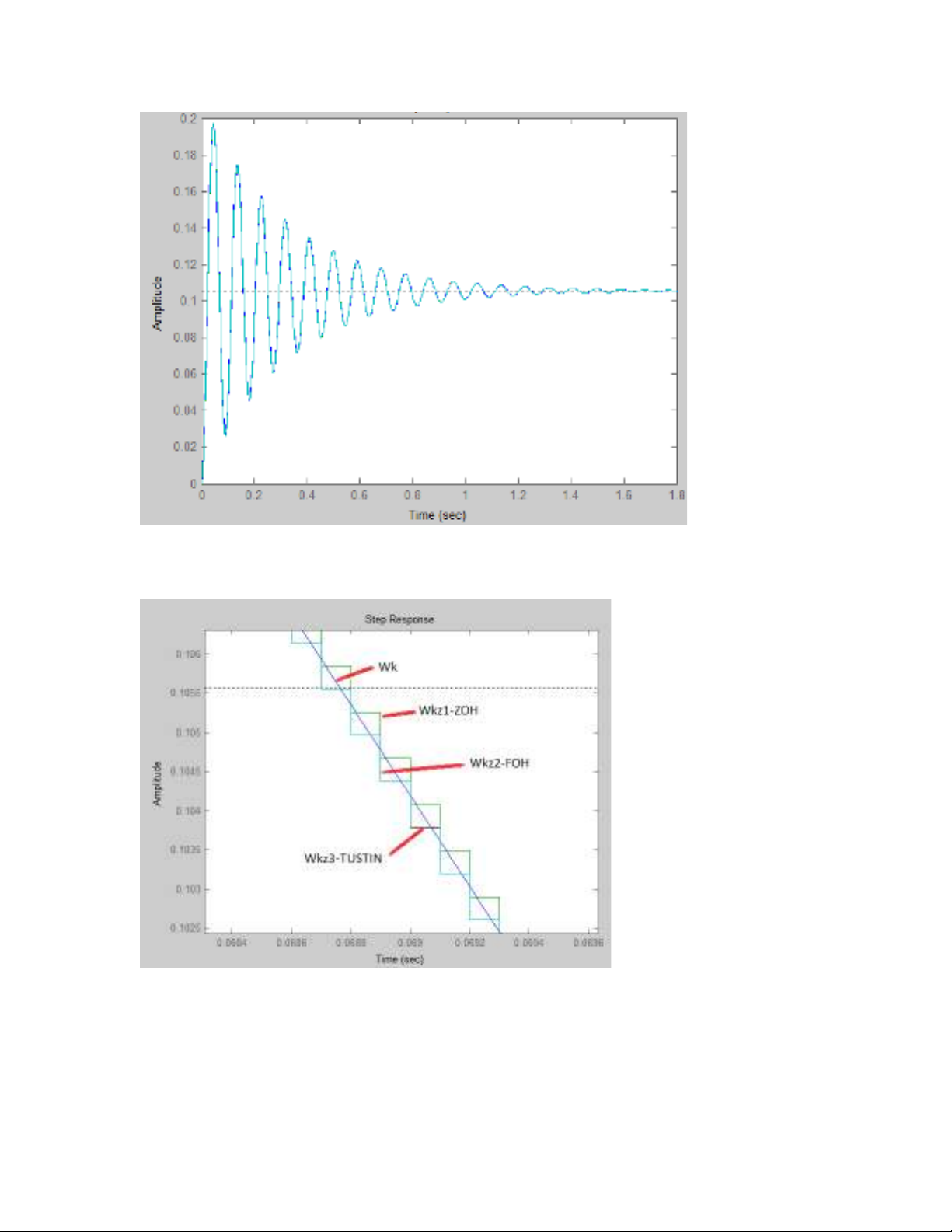
Vì đ chính xác c a máy tính là cao nên n u đ quan sát trên kho ng th iộ ủ ế ể ả ờ
gian r ng s không th th y đ c s khác bi t gi a các ph ng pháp.Taộ ẽ ể ấ ượ ự ệ ữ ươ
phóng to hình trên:
4. Xây d ng mô hình tr ng thái c a ĐCMC trên mi n th i gian liên t c. S d ngự ạ ủ ề ờ ụ ử ụ
ph ng pháp đã h c (m c 1.3.2c, tài li u [1]) đ gián đo n hóa mô hình v i giươ ọ ụ ệ ể ạ ớ ả
thi t chu kỳ trích m u ế ẫ T=0,01s và T=0,1s.
Nguy n Th Đ c-20090812ễ ế ứ
ĐK&TĐH4-K54