BỘ 30 ĐỀ THI
VÀO LỚP 10
MÔN TOÁN
NĂM 2020 - CÓ ĐÁP ÁN
1. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT An Giang
2. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Bắc Giang
3. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Bến Tre
4. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Bình Phước
5. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Bình Thuận
6. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Cao Bằng
7. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Đồng Nai
8. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Hà Nam
9. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Hà Nội
10. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Hải Dương
11. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Hải Phòng
12. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Hòa Bình
13. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Khánh Hòa
14. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Lạng Sơn
15. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Long An
16. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Nam Định
17. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Ninh Bình
18. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Quảng Ninh
19. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Sóc Trăng
20. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Thái Bình
21. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Thanh Hóa
22. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Thành phố Đà Nẵng
23. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Thừa Thiên Huế
24. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Tiền Giang
25. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT TP.HCM
26. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở
GD&ĐT Vĩnh Phúc
27. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở GD-
KH&CN Bạc Liêu
28. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Sở Giáo
dục và Đào tạo
29. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Trường
Đại học KHTN ĐHQG Hà Nội
30. Đề tuyển sinh vào lớp 10 THPT môn Toán năm 2020-2021 có đáp án - Trường
PT Năng khiếu ĐHQG TP.HCM
SỞ GIÁO DỤC VÀ ĐÀO TẠO KỲ THI TUYỂN SINH VÁO LỚP 10 THPT
AN GIANG Năm học: 2020 – 2021
Khóa ngày: 18/07/2020
ĐỀ CHÍNH THỨC Môn thi: TOÁN
(Đề thi gồm có 01 trang) Thời gian làm bài: 120 phút, không kể thời gian giao đề
Câu 1. (3,0 điểm)
Giải các phương trình và hệ phương trình sau đây:
a.
3 3 3;x−=
b.
7;
22
xy
xy
+=
−+ =
c.
42
3 4 0;xx− −=
Câu 2. (2,0 điểm)
Cho hàm số
2
yx=
có đồ thị là parabol
( )
P
.
a. Vẽ đồ thị
( )
P
trên hệ trục tọa độ.
b. Viết phương trình đường thẳng
( )
d
có hệ số góc bằng
và cắt parabol
( )
P
tại điểm có
hoành độ bằng
1
.
c. Với
( )
d
vừa tìm được, tìm giao điểm còn lại của
( )
d
và
( )
P
.
Câu 3. (2,0 điểm)
Cho phương trình bậc hai
( )
2
2 10 ;x xm− + −= ∗
với
m
là tham số.
a. Tìm tất cả các giá trị của
m
để phương trình
( )
∗
có nghiệm.
b. Tính theo
m
giá trị của biểu thức
33
12
Ax x= +
với
12
;xx
là hai nghiệm của phương trình
( )
∗
. Tìm giá trị nhỏ nhất của
A
.
Câu 4. (2,0 điểm)
Cho tam giác
ABC
có ba góc đều nhọn và nội tiếp trong đường tròn
( )
O
. Vẽ các đường cao
'; '; 'AA BB CC
cắt nhau tại
H
.
a. Chứng minh rằng tứ giác
''AB HC
là tứ giác nội tiếp.
b. Kéo dài
'AA
cắt đường tròn
( )
O
tại điểm
D
. Chứng minh rằng tam giác
CDH
cân.
Câu 5. (1,0 điểm)
Cho
ABCD
là hình vuông có cạnh
1dm
. Trên cạnh
AB
lấy một
điểm
E
. Dựng hình chữ nhật
CEFG
sao cho điểm
D
nằm trên cạnh
FG
. Tính diện tích hình chữ nhật
CEFG
(hình vẽ bên)
-------- HẾT --------
1
dm
F
G
C
D
A
B
E
ĐÁP ÁN VÀ LỜI GIẢI CHI TIẾT
Bài 1 (3,0 điểm):
a)
( )
3 3 3 3 1 3 11 2x x xx− = ⇔ − = ⇔ −=⇔ =
Vậy PT có nghiệm duy nhất
2x=
b)
7 39 3 4
2 2 7 37 3
xy y y x
x y xy x y
+= = = =

⇔⇔⇔

−+ = + = += =

Vậy HPT có nghiệm duy nhất
( ) ( )
; 4;3xy =
c)
42
3 40xx− −=
Đặt
2
tx=
. Điều kiện
0t≥
PT đã cho trở thành:
2
3 40tt− −=
(1)
PT (1) có các hệ số:
1; 3; 4ab c= =−=−
Vì
1 (3) (4) 0abc− + = −− +− =
nên PT (1) có hai nghiệm phân biệt
11t= −
(loại) ;
2
( 4) 4
1
c
ta
− −−
= = =
Với
2
44 2tx x=⇒ =⇔=±
Vậy PT đã cho có hai nghiệm phân biệt:
12
2; 2xx= = −
Bài 2 (2,0 điểm): Cho hàm số
2
yx=
có đồ thị là Parabol (P).
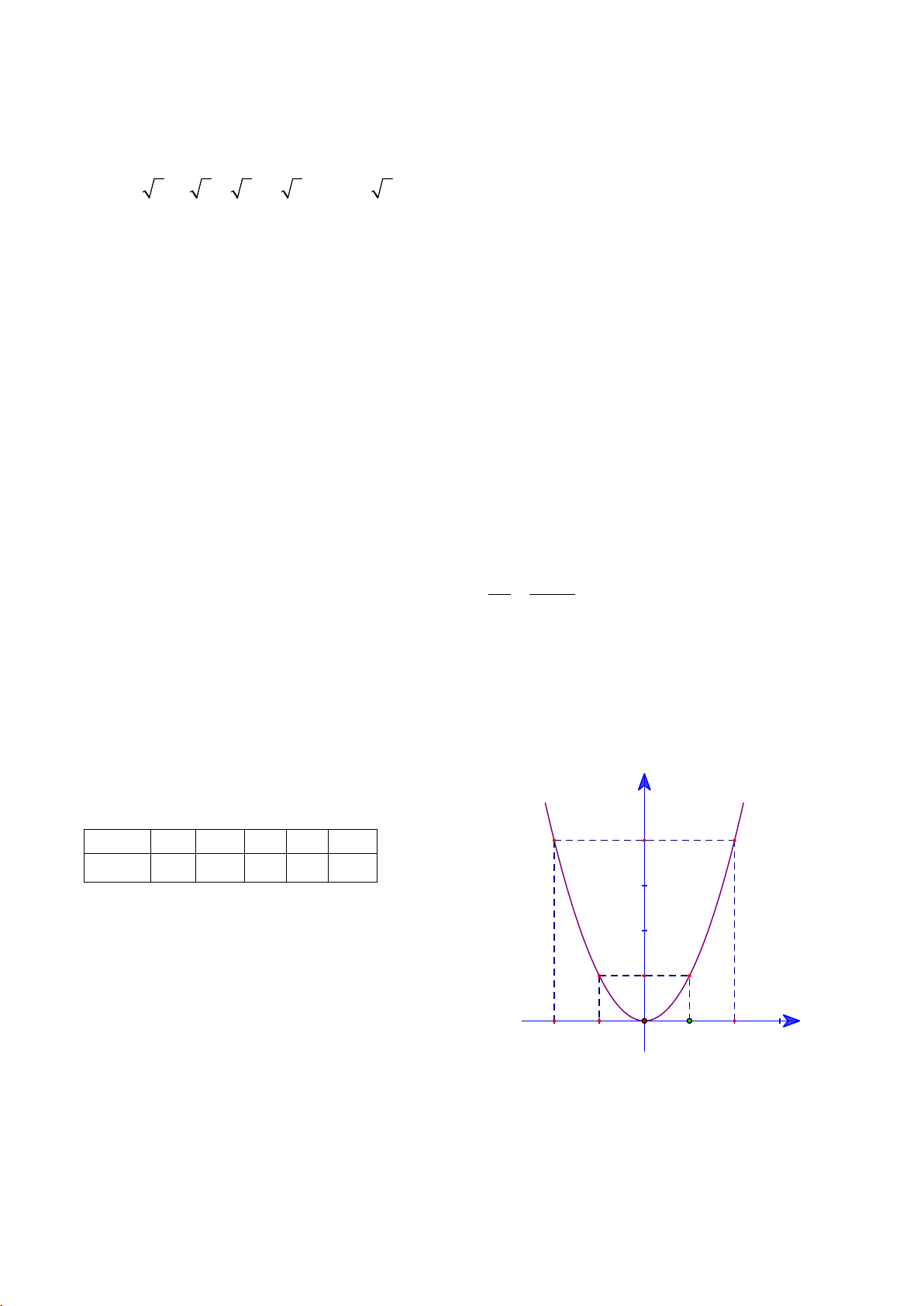
a) Vẽ đồ thị (P):
Bảng giá trị đặc biệt:
x
- 2
- 1
0
1
2
2
yx=
4
1
0
1
4
Vẽ đồ thị:
b) PT đường thẳng (d) có dạng:
y ax b= +
Vì (d) có hệ số góc bằng – 1 nên
1 ( ):a dy xb=−⇒ =−+
Vì (d) cắt (P) tại điểm có hoành độ bằng 1 nên thay
1x=
vào hàm số
2
yx=
ta được:
2
11y= =
(
P
)
x
y
4
1
-2
-1
2
O
1