LÊ QUANG XE
LUYỆN THI THPT QUỐC GIA
BỘ 20 ĐỀ
8+
LƯU HÀNH NỘI BỘ
NĂM HỌC 2021 −2022
MỤC LỤC
Đề số 1 1
Đề số 2 12
Đề số 3 23
Đề số 4 34
Đề số 5 45
Đề số 6 56
Đề số 7 67
Đề số 8 78
Đề số 9 89
Đề số 10 100
Đề số 11 111
Đề số 12 122
Đề số 13 133
Đề số 14 143
Đề số 15 154
Đề số 16 165
Đề số 17 176
Đề số 18 188
Đề số 19 199
Đề số 20 210
219 i/219 pLê Quang Xe – Ô0967.003.131
MỤC LỤC NƠI NÀO CÓ Ý CHÍ, NƠI ĐÓ CÓ CON ĐƯỜNG
ii
219 ii/219 pLê Quang Xe – Ô0967.003.131
PHÁT TRIỂN ĐỀ THAM KHẢO 2022 NƠI NÀO CÓ Ý CHÍ, NƠI ĐÓ CÓ CON ĐƯỜNG
1
BỘ GIÁO DỤC & ĐÀO TẠO
TRƯỜNG THPT NGUYỄN TẤT THÀNH
GV: LÊ QUANG XE - 0967.003.131
ĐỀ SỐ 1
PHÁT TRIỂN ĐỀ THAM KHẢO 2022
NĂM HỌC 2021 - 2022
Môn: Toán
Thời gian làm bài: 90 phút
PHÁT TRIỂN ĐỀ THAM KHẢO 2022
dCâu 1. Trong các mệnh đề sau, mệnh đề nào đúng?
ASố phức z= 2 −3icó phần thực là 2và phần ảo là −3i.
BSố phức z= 2 −3icó phần thực là 2và phần ảo là −3.
CSố phức z= 2 −3icó phần thực là 2và phần ảo là 3i.
DSố phức z= 2 −3icó phần thực là 2và phần ảo là 3.
ÊLời giải.
Một số phức z=a+bi thì alà phần thực, blà phần ảo và ilà đơn vị ảo.
Chọn đáp án B
dCâu 2. Trong không gian Oxyz, mặt cầu tâm I(1; 2; 3) đi qua điểm A(1; 1; 2) có phương trình
là A(x−1)2+ (y−1)2+ (z−2)2= 2.B(x−1)2+ (y−2)2+ (z−3)2= 2.
C(x−1)2+ (y−2)2+ (z−3)2=√2.D(x−1)2+ (y−1)2+ (z−2)2=√2.
ÊLời giải.
Bán kính R=IA =√2nên phương trình mặt cầu là (x−1)2+ (y−2)2+ (z−3)2= 2.
Chọn đáp án B
dCâu 3. Trong các hàm số dưới đây, hàm số nào có đồ thị đi qua điểm M(1; 0)?
Ay=x3+ 3x2−3.By=2x−2
x2−1.
Cy=x4−3x2+ 2.Dy= (x−1)√x−2.
ÊLời giải.
Đáp án đúng y=x4−3x2+ 2.
Chọn đáp án C
dCâu 4. Cho một mặt cầu có diện tích là Svà thể tích là V. Tính bán kính Rcủa mặt cầu.
AR=3V
S.BR=S
3V.CR=4V
S.DR=V
3S.
ÊLời giải.
Ta có V=4
3πR3và S= 4πR2.
Suy ra V
S=R
3hay R=3V
S.
Chọn đáp án A
219 1/219 pLê Quang Xe – Ô0967.003.131
ĐỀ SỐ 1 NƠI NÀO CÓ Ý CHÍ, NƠI ĐÓ CÓ CON ĐƯỜNG
2
dCâu 5. Họ nguyên hàm của hàm số f(x) = sin 5x+ 2 là
A5 cos 5x+C.B−1
5cos 5x+ 2x+C.
C1
5cos 5x+ 2x+C.Dcos 5x+ 2x+C.
ÊLời giải.
Ta có: Zf(x)dx =Z(sin 5x+ 2)dx =−1
5cos 5x+ 2x+C.
Chọn đáp án B
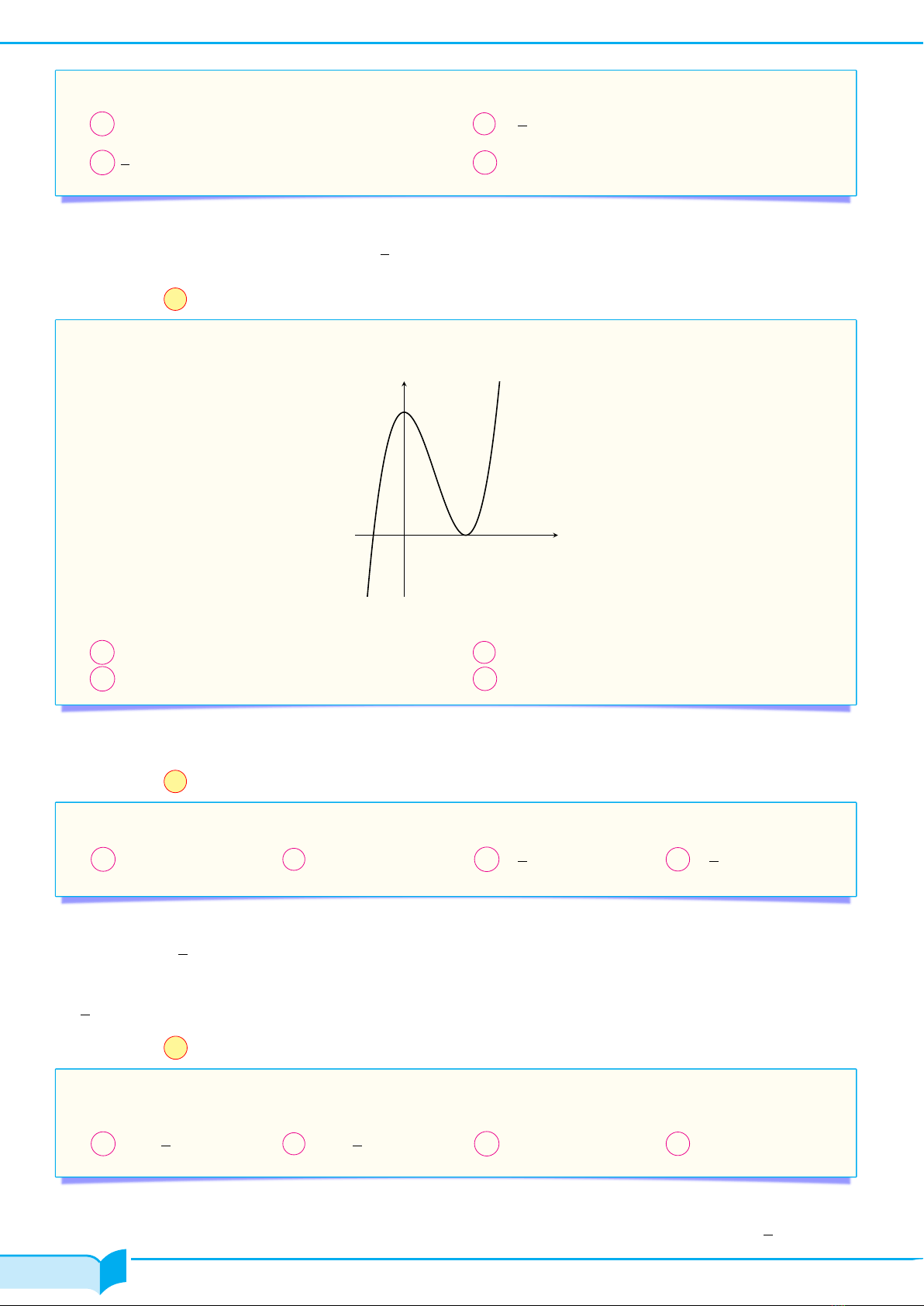
dCâu 6. Cho hàm số y=f(x)có đồ thị như hình vẽ bên dưới.
x
y
O
−1 2
4
Mệnh đề nào sau đây đúng ?
AHàm số đạt cực đại tại x= 2.BHàm số đạt cực tiểu tại x= 2.
CHàm số đạt cực đại tại x= 4.DHàm số đạt cực tiểu tại x= 0.
ÊLời giải.
Dựa vào đồ thị.
Chọn đáp án B
dCâu 7. Bất phương trình log0,5(2x−3) >0có tập nghiệm là
A(−∞; 2).B(2; +∞).CÅ3
2; +∞ã.DÅ3
2; 2ã.
ÊLời giải.
Điều kiện: x > 3
2
log0,5(2x−3) >0⇔2x−3<1⇒x < 2
⇒3
2< x < 2
Chọn đáp án D
dCâu 8. Thể tích của khối chóp có diện tích đáy Bvà chiều cao hđược tính theo công thức
nào sau đây?
AV=1
2Bh.BV=1
3Bh.CV= 3Bh.DV=Bh.
ÊLời giải.
Thể tích của khối chóp có diện tích đáy Bvà chiều cao hđược tính theo công thức V=1
3Bh.
219 2/219 pLê Quang Xe – Ô0967.003.131