Đề thi học kì 1 Toán 8 Cánh diều
I. TRẮC NGHIỆM KHÁCH QUAN: (3,0 điểm)
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Hãy viết chữ cái in hoa đứng trước phương án đúng duy nhất trong mỗi câu sau vào bài làm.
Câu 1 : Kết quả thu gọn của A= (2x2-4xy+5)+(3xy-5) l
A. 2x2-x2y2
B.2x2-7xy
C.2x2-xy
D.2x2-xy+10
Câu 2 : Thương của phép chia (12x4y + 4x3 – 8x2y2) : (4x2) bằng
B. 3x4y + x3– 2x2y2
B. -12x2y + 4x – 2y2
C. 3x2y + x – 2y2
D. -3x2y + x – 2y2
Câu 3. Kết quả rút gọn phân thức l
A. B. C. D.
Câu 4: Thực hiện phép tính ta được
A. B. C. D.
Câu 5. Cho hm số y = f(x) = 2x2 - 1. Khẳng định no sau đây l đúng?
A. f(-1) = -3.
B. f(1) = 1.
C. f(-1) = -1.
D. f(1) = 3.
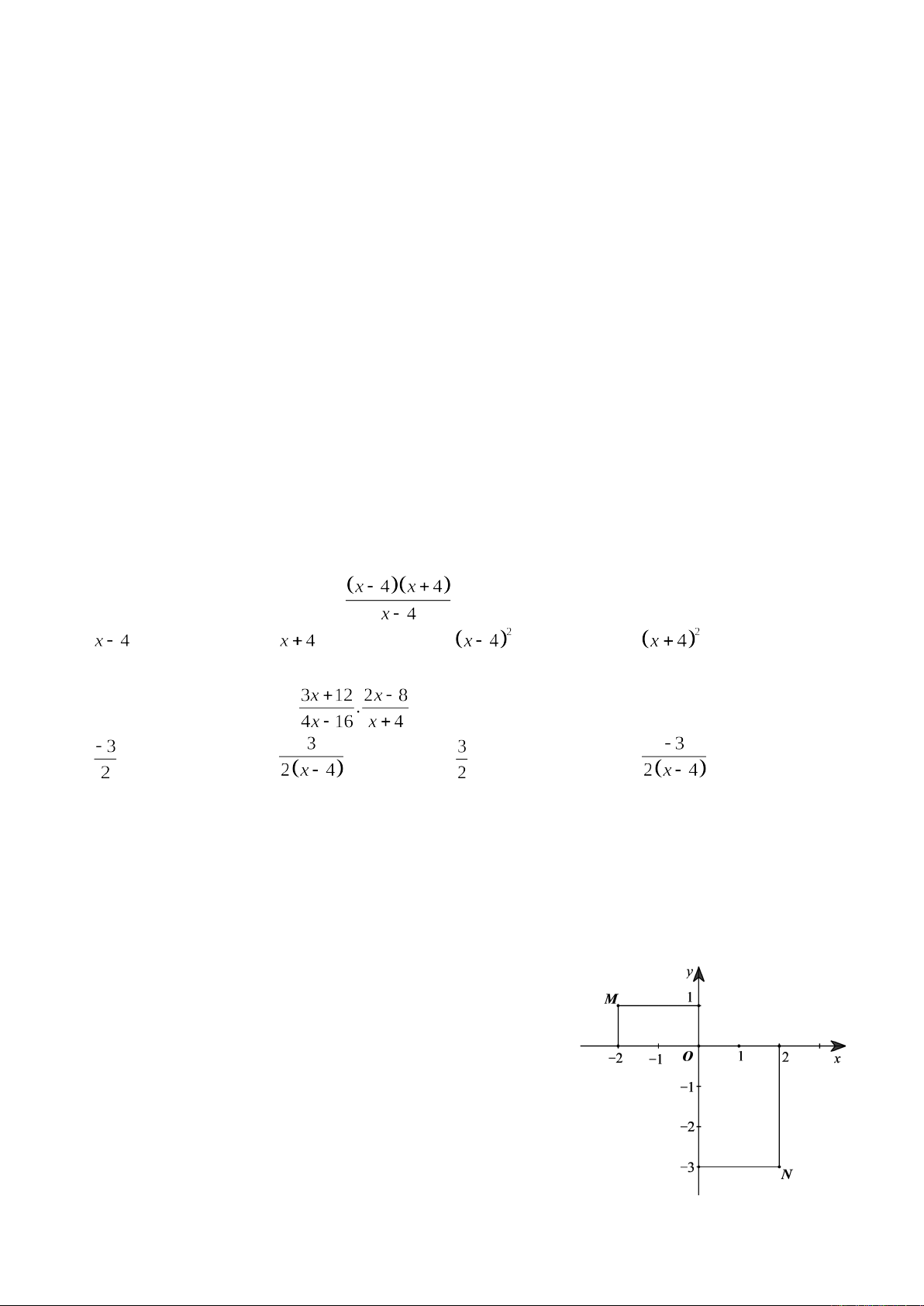
Câu 6. Cho điểm A v B trong mặt phẳng tọa độ Oxy như
hình bên. Khẳng định no sau đây l đúng?
A. N (-3; 2).
B. N(2; -3).
C. M (1; -2).
D. M (-1; 2).
Câu 7. Cho hai đường thẳng d: y = ax + b (a ≠ 0) v d': y = a'x + b' (a' ≠ 0). Với điều kiện no sau
đây thì hai đường thẳng d v d' song song?
A. a = a'.
B. a = a' v b = b'.
C. a ≠ a'.
D. a = a' v b ≠ b'.
Câu 8. Góc tạo bởi đường thẳng y = -2x + 1 với trục Ox l
A. góc nhọn.
B. góc vuông.
C. góc tù.
D. góc bẹt.
Câu 9. TZng số cạnh bên v cạnh đ[y của một hình chóp tứ gi[c đều l
A. 4.
B. 6.
C. 8.
D. 10.
Câu 10 : Hình chóp tam gi[c đều có cạnh đ[y 20dm, chiều cao mặt bên 10dm, có diện tích xung
quanh l:
A. 100 dm3B. 100 dm2C. 300 dm3D. 300 dm2
Câu 11. Một hình thang vuông có một góc bằng 75° góc còn lại không vuông của hình thang đó
có số đo l
A. 25°.
B. 75°.
C. 105°.
D. 125°.
Câu 12. Hình thoi cần thêm yếu tố no để trở thnh hình vuông?
A. Hai đường chéo vuông góc.
B. Hai đường chéo bằng nhau.
C. Hai cạnh kề bằng nhau.
D. Một đường chéo l tia phân gi[c của một góc.
II. TỰ LUẬN : (7,0 điểm)
Câu 1. (1 điểm) Rút gọn c[c biểu thức sau
a)
b)
Câu 2. (1 điểm) Phân tích đa thức thnh nhân tử
a)
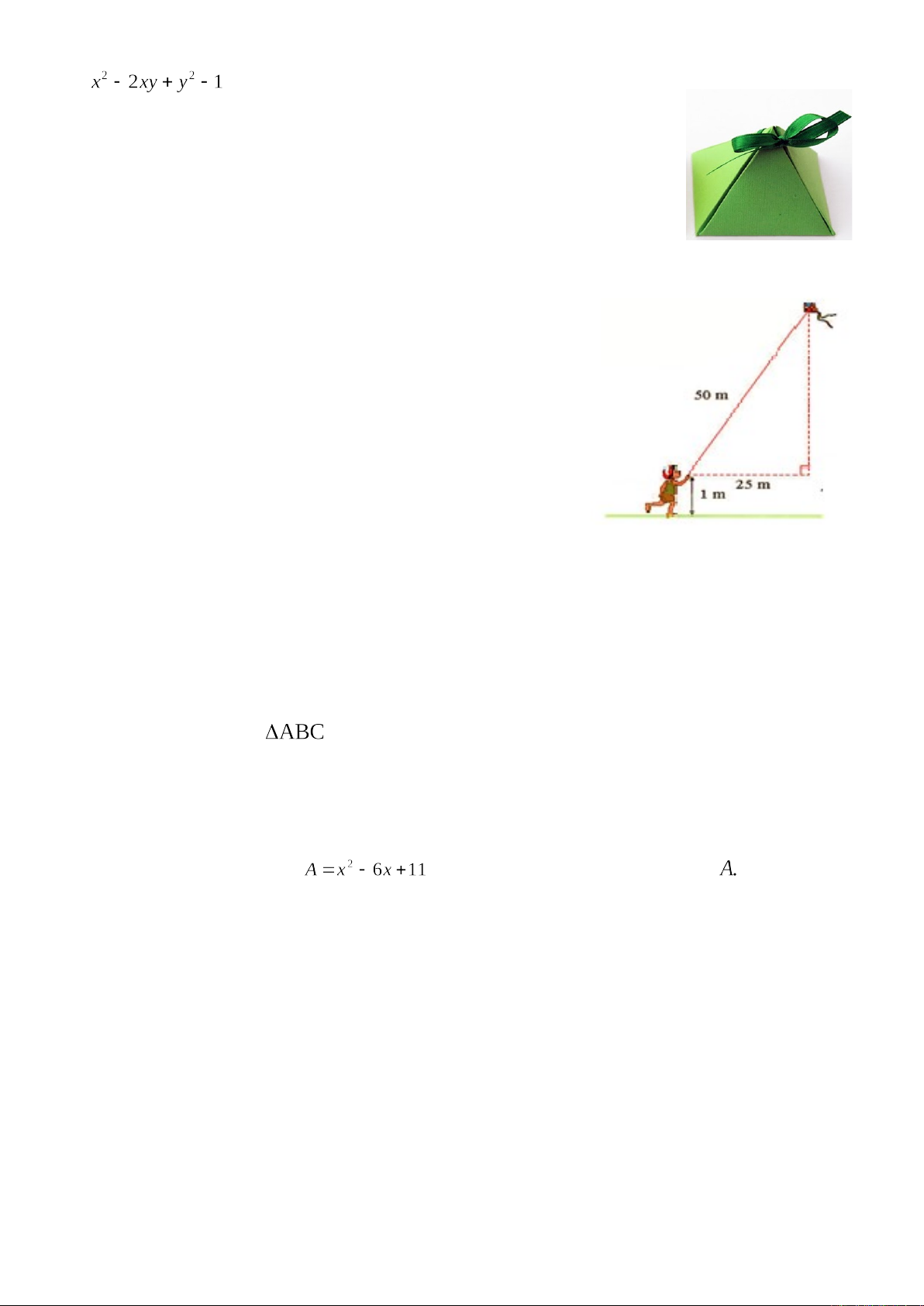
b)
Câu 3. (1 điểm)
a) Bạn Đo dự định gấp một hộp qu hình chóp tứ gi[c đều có cạnh đ[y
bằng 6cm v chiều cao l 4cm, để đựng món qu tặng sinh nhật bạn Nam.
(xem hình ảnh minh họa). Thể tích tối đa m hộp qu có thể chứa được l
bao nhiêu?
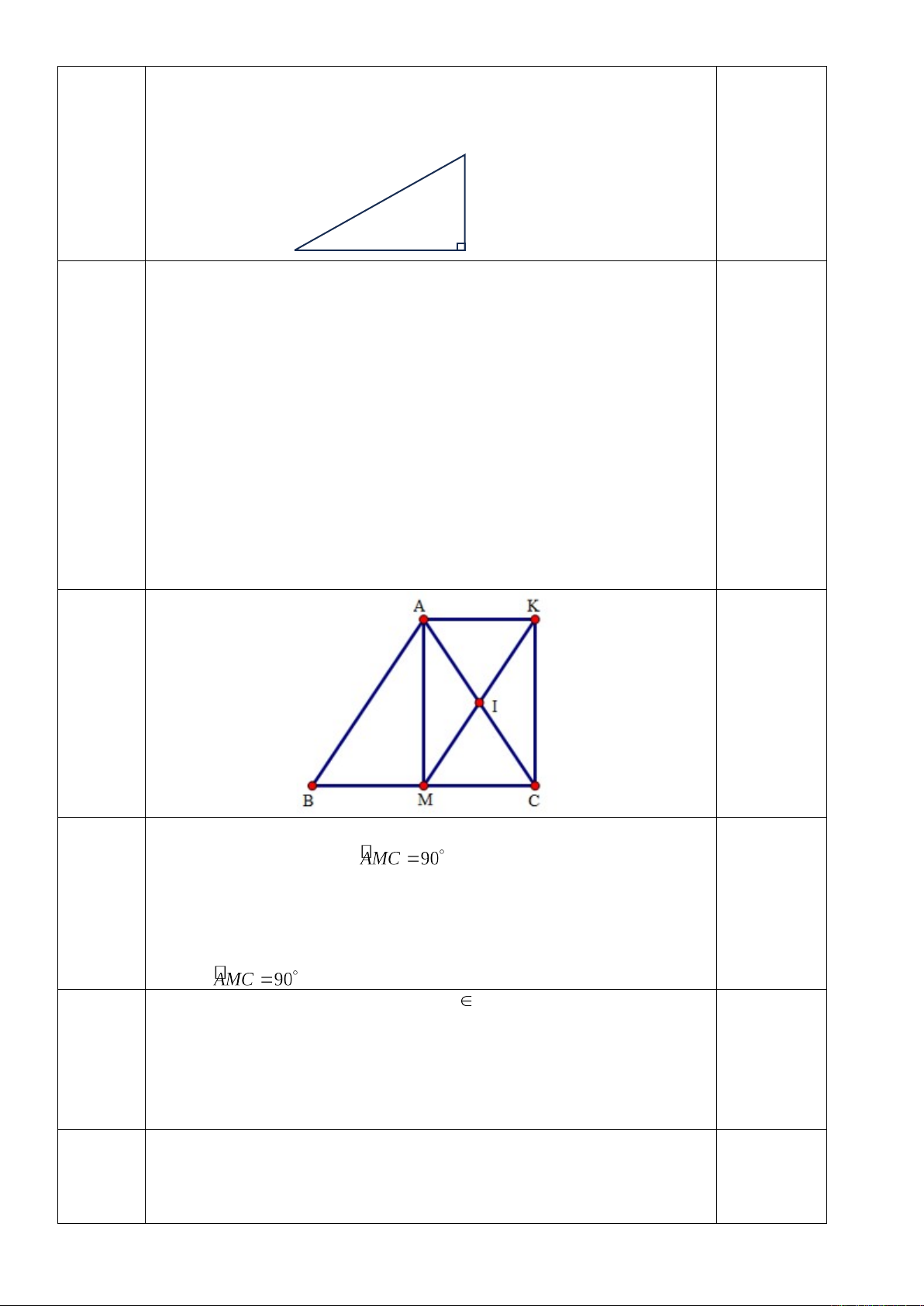
b) Một bạn học sinh thả diều ngoi đồng, cho biết đoạn dây
diều từ tay bạn đến diều di 50m v bạn đứng c[ch nơi diều
được thả lên theo phương thẳng đứng l 25m. Tính độ cao của
con diều so với mặt đất, biết tay bạn học sinh c[ch mặt đất 1m.
(kết quả làm tròn đến phần mười.)
Câu 4. (1 điểm) Hm chi phí đơn giản nhất l hm chi phí bậc
nhất y = ax + b, trong đó b biểu thị chi phí cố định của hoạt
động kinh doanh v hệ số a biểu thị chi phí của mỗi mặt hng được sản xuất. Giả sử rằng một
xưởng sản xuất xe đạp có chi phí cố định hằng ngy l 36 triệu đồng v mỗi chiếc xe đạp có chi
phí sản xuất l 1,8 triệu đồng.l
a) Viết công thức của hm số bậc nhất biểu thị chi phí y (triệu đồng) để sản xuất x (xe đạp) trong
một ngy.
b) Có thể sản xuất bao nhiêu chiếc xe đạp trong ngy, nếu chi phí trong ngy đó l 72 triệu đồng?
Câu 5: (2,5 điểm) Cho cân tại A có đường trung tuyến AM, gọi I l trung điểm của AC.
Lấy điểm K sao cho I l trung điểm của đoạn thẳng MK.
a) Chứng minh tứ gi[c AMCK l hình chữ nhật
b) Tứ gi[c AKMB l hình gì? Vì sao?
c) Tìm điều kiện của tam gi[c ABC để tứ gi[c AMCK l hình vuông.
Câu 6. (0,5đ) Cho biểu thức . Tính gi[ trị nhỏ nhất của biểu thức
..................HẾT................
I. TRẮC NGHIỆM (0,25 điểm/câu)
Câu 1 2 3 4 5 6 7 8 9 10 11 12
Đáp án C C B B C B D C C D C B
II.TỰ LUẬN
Câu Đáp án Điểm
1
a)
0,25đ
0,25đ
b)
0,25đ
0,25đ
2
Câu 2. (1 điểm) Phân tích đa thức thnh nhân tử
a)
=5x(x-2)+3(x-2)
=(x-2)(5x+3)
0,25đ
0,25đ
b) 0,25đ
0,25đ
3
a) Thể tích của hộp qu l:
0,5đ
b) Áp dụng định lý Pytago vo tam gi[c vuông ABC, có:
Vậy độ cao con diều so với mặt đất l 43,3 + 1 = 44,3m
0,25đ
0,25đ
(Bài làm học sinh không có hình và đặt tên thì không chấm)
4
a) Công thức của hm số bậc nhất biểu thị chi phí y (triệu đồng) để
sản xuất x (xe đạp) trong một ngy l:
y = 1,8x + 36 (triệu đồng).
b) Do chi phí trong ngy đó l 72 triệu đồng nên y = 72 (triệu đồng).
Thay y = 72 vo công thức y = 1,8x + 36 ta có:
1,8x + 36 = 72
1,8x = 36
x = 20
Vậy với chi phí l 72 triệu đồng thì trong ngy đó có thể sản xuất
được 20 chiếc xe đạp.
0,5đ
0,5đ
5
a) ΔABC cân tại A có AM l đường trung tuyến
=> AM l đường cao =>
Xét tứ gi[c AMCK có:
I l trung điểm AC (gt)
I l trung điểm MK (K l điểm đối xứng với M qua I)
=> AMCK l hình bình hnh
Lại có => AMCK l hình chữ nhật
0,25đ
0,5đ
0,25đ
b) Ta có: AK//MC (AKCM l hcn), B MC
=> AK//BM (1)
Lại có: AK=MC (AKCM l hcn), BM=MC (M l trung điểm của
AC)
=>AK=BM(2)
Từ (1) v (2)=> AKMB l hình bình hnh
0,25đ
0,5đ
0,25đ
c) Hcn AMCK l hình vuông AM=MC
AM=1/2BC
∆ABC vuông tại A (theo tính chất đường trung tuyến ứng với
cạnh huyền trong tam gi[c vuông)
0,25đ
C
AB