1
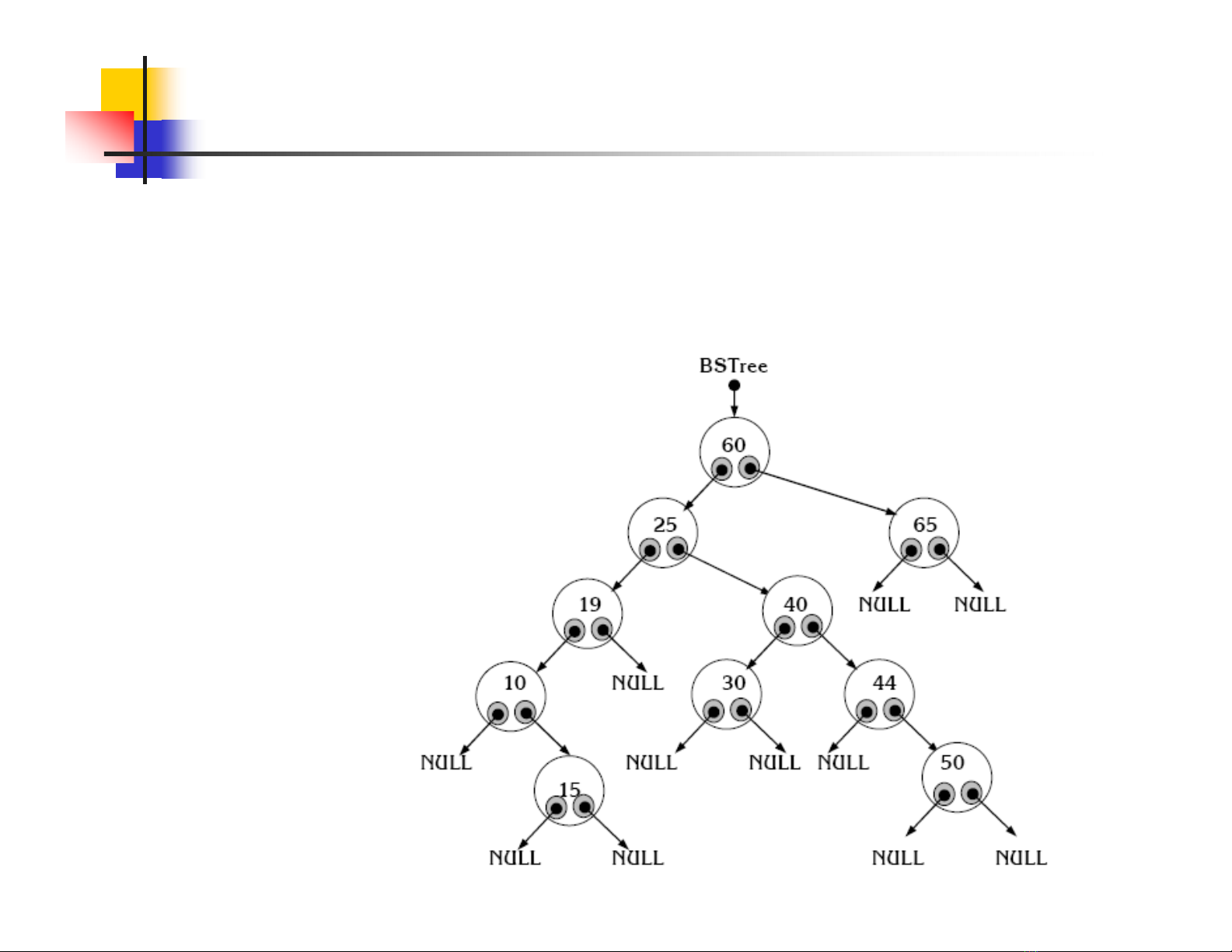
2.3. Cây nhị phân tìm kiếm (Binary Searching Tree)
2.3.1. Khái niệm –Cấu trúc dữ liệu
Cây nhị phân tìm kiếm là cây nhị phân trong đó tại mỗi nút,
khoá của nút đang xét lớn hơn khóa của tất cả các nút thuộc
cây con trái và nhỏ hơn khoá của tất các nút thuộc cây con
phải.
Cấu trúc dữ liệu của cây nhị phân tìm kiếm là cấu trúc dữ liệu
biểu diễn cây nhị phân nói chung.
struct TNode
{
int Info;
struct TNode *pL,*pR;
};
2
2.3. Cây nhị phân tìm kiếm (Binary Searching Tree)
2.3.2. Các thao tác trên cây nhị phân tìm kiếm
2.3.2.a. Thêm vào một phần tử X vào cây
2.3.2.b. Tạo một cây NPTK
2.3.2.c. Duyệt cây
2.3.2.d. Tìm một phần tử X trong cây
2.3.2.e. Huỷ một phần tử có
khoá X
3
2.3.2.a. Thêm vào một phần tử X vào cây
Việc thêm một phần tử x vào cây phải đảm bảo điều kiện ràng
buộc của CNPTK:
-* Mọi số thuộc cây con trái của nút đó đều nhỏ hơn số ứng với
nút đó
-* Mọi số thuộc cây con phải của nút đó đều lớn hơn số ứng với
nút đó
Hàm insert trả về giá trị -1: khi không đủ bộ nhớ.
0: khi gặp nút trùng.
1: khi thực hiện thành công.
4
int InsertTree(TREE &T,int k)
{
if (T!=NULL)
{ //neu can ca so trung nhau thi bo dong ngay duoi
if (T->Info==k) return 0;
if (T->Info>k) return InsertTree(T->pL,k);
else return InsertTree(T->pR,k);
}
else
{ T=(TREE)malloc(sizeof(TNode));
if (T==NULL) return -1;
T->Info=k;
T->pL=T->pR=NULL;
return 1;
}
}
5
2.3.2.b. Tạo một cây NPTK: Ta có thể tạo CNPTK bằng cách lặp
lại quá trình thêm 1 phần tử vào một cây rỗng
void CreateTree(TREE &T)
{ T=NULL;
int k;
cout<<"\nIn put n=";
cin>>n;
for (int i=1;i<=n;i++)
{
cin>>k;
InsertTree(T,k);
}
}