1
Môn: C U TRÚC D LI UẤ Ữ Ệ
Ch ng 5: CÂY (TREE)ươ
2
N I DUNG CH NG 5Ộ ƯƠ
1. Khái ni m cây – Bi u di n câyệ ể ễ
2. Cây nh phân (Binary Tree)ị
1. Đ nh nghĩaị
2. Bi u di n và các thao tácể ễ
3. Cây nh phân tìm ki m (Binary Searching Tree)ị ế
3. Cây cân b ng (Balanced Tree)ằ
1. Đ nh nghĩa – C u trúc d li uị ấ ữ ệ
2. Các thao tác trên cây cân b ngằ
BÀI T PẬ
3
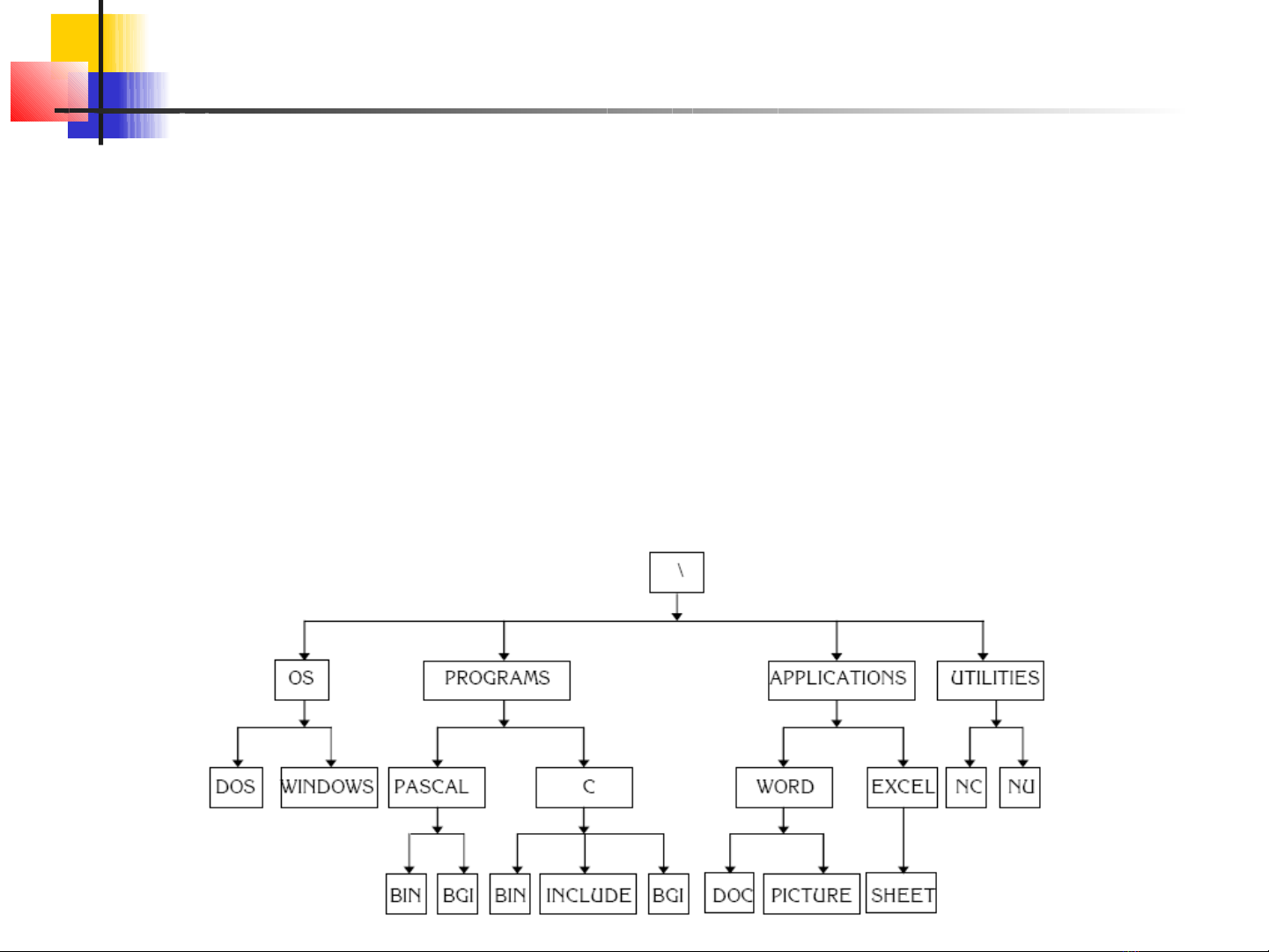
1.Khái ni m cây – Bi u di n câyệ ể ễ
1.1 Đ nh nghĩa câyị
1.2. M t s khái ni m liên quanộ ố ệ
1.2.a. B c c a 1 câyậ ủ
1.2.b. B c c a 1 nútậ ủ
1.2.c. Nút g cố
1.2.d. Nút k t thúc ế
1.2.e. Nút trung gian
1.2.f. M c c a 1 nútứ ủ
1.2.g. Chi u cao (chi u sâu) c a 1 câyề ề ủ
1.2.h. Nút tr c, nút sau c a 1 nútướ ủ
1.2.i. Nút cha, nút con c a 1 nútủ
1.2.j. Chi u dài đ ng đi c a 1 nútề ườ ủ
1.2.k. Chi u dài đ ng đi c a 1 câyề ườ ủ
1.2.l. R ngừ
4
1.Khái ni m cây – Bi u di n cây (tt)ệ ể ễ
1.1 Đ nh nghĩa câyị
Cây là m t t p h p các ph n t (nút) đ c t ch c và có các ộ ậ ợ ầ ử ượ ổ ứ
đ c đi mặ ể
Ho c là t p h p r ng (cây r ng)ặ ậ ợ ỗ ỗ
Ho c là t p h p khác r ng trong đó có ặ ậ ợ ỗ 1 nút duy nh t ấ làm
nút g c ố(Root’s Node), các nút còn l i đ c phân thành ạ ượ
các nhóm trong đó m i nhóm là 1 cây con (Sub-Tree)ỗ
Các cây con cũng có th là ểt p r ngậ ỗ hay khác r ng ỗtrong đó
có 1 nút là g c cây con.ố
5
1.Khái ni m cây – Bi u di n cây (tt)ệ ể ễ
1.2. M t s khái ni m c b nộ ố ệ ơ ả
1.2.a. B c c a 1 nútậ ủ
B c c a 1 nút (node’s degree) là s cây con c a nút đóậ ủ ố ủ
1.2.b. B c c a 1 câyậ ủ
B c c a 1 cây (tree’s degree) là b c l n nh t c a các nút ậ ủ ậ ớ ấ ủ
trong cây
Cây có b c N g i là cây N phânậ ọ
1.2.c. Nút g cố
Nút g c (root’s tree) là nút không ph i là nút g c cây con c a ố ả ố ủ
b t kỳ 1 cây con nào khác trong cây (nút không làm g c cây ấ ố
con)
1.2.d. Nút lá
Nút k t thúc hay còn g i nút lá (leaf’s node) là nút có b c = 0 (nút ế ọ ậ
không có nút cây con)