
Ph ng trình l ng giácươ ượ NXT - FIT
L ng giácượ
Ph n 1: Hàm s l ng giácầ ố ượ
A. Ki n th c c n nhế ứ ầ ớ
1. Các h ng đ ng th c c b nằ ẳ ứ ơ ả
a)
1cossin 22 =+ xx
b)
x
x
xcos
sin
tan =
c)
x
x
xsin
cos
cot =
d)
x
x2
2
cos
1
tan1 =+
e)
x
x2
2
sin
1
cot1 =+
f)
1cot.tan
=
xx
2. Giá tr c a các hàm l ng giác cung liên quan đ c bi tị ủ ượ ặ ệ
a) Hai cung đ i nhauốb) Hai cung bù nhau c) Hai cung khác nhau 2
π
xx
xx
xx
xx
cot)cot(
tan)tan(
sin)sin(
cos)cos(
−=−
−=−
−=−
=−
xx
xx
xx
xx
cot)cot(
tan)tan(
cos)cos(
sin)sin(
−=−
−=−
−=−
=−
π
π
π
π
xx
xx
xx
xx
cot)2cot(
tan)2tan(
cos)2cos(
sin)2sin(
=+
=+
=+
=+
π
π
π
π
d) Hai cung khác nhau
π
e) Hai cung ph nhauụ
xx
xx
xx
xx
cot)cot(
tan)tan(
cos)cos(
sin)sin(
=+
=+
−=+
−=+
π
π
π
π
xxxx
xxxx
tan
2
cot ; cot
2
tan
sin
2
cos ; cos
2
sin
=
−=
−
=
−=
−
ππ
ππ
B. Bài t pậ
1. Tìm các giá tr c a ị ủ
α
đ bi u th c sau đ t giá tr nh nh t. Tìm giá tr nh nh t đó.ể ể ứ ạ ị ỏ ấ ị ỏ ấ
αα
cos1
1
;
sin1
1
−
=
+
=BA
2. Xét d u c a các bi u th c sau:ấ ủ ể ứ
a)
oo 132sin123sin −
b)
oo 316cot304cot −
3. Rút g n các bi u th c sau:ọ ể ứ
a)
oooo 540cos3990sin41170cos2540tan5 −++
b)
3
19
cos2
4
13
tan3
6
25
sin3
πππ
+−
c)
oooo 75sin55sin35sin15sin 2222 +++
d)
oooo 75cos55cos35cos15cos 2222 +++
e)
12
11
sin
12
9
sin
12
7
sin
12
5
sin
12
3
sin
12
sin 222222
ππππππ
+++++
f)
12
11
cos
12
9
cos
12
7
cos
12
5
cos
12
3
cos
12
cos 222222
ππππππ
+++++
g)
++−+
+−+ aaaa 2
3
tan)2cot(
2
cos)sin(
π
π
π
π
h)
aaaaA 2224 cos.sincossin ++=
i)
2
cos.
2
sin
2
tan
1
2
cos
2
sin
2
aaa
aa
B
−
−
+
=
j)
oo
ooo
C342cot252tan
156cos530tan).260tan(696cos
22
22
+
−−+
=
k)
( )
2
2
7cot
4
13
cot
2
7
tan
4
17
tan
−++
−+ bb
π
πππ
2K2+ - 1 -

Ph ng trình l ng giácươ ượ NXT - FIT
l)
−
+
−
+
−
−
+
−
+
−
x
x
x
x
x
x
x
x
cos1
cos1
cos1
cos1
sin1
sin1
sin1
sin1
m)
)tan1(cos)cot1(sin 33 aaaa +++
n)
bb
b
cottan
tan
+
o)
a
aa
4
44
cos
sincos1 −−
p)
+−
−
−−−
xxx
xxx
2
3
cot).cot(.
2
sin
)2sin().2cos().sin(
π
π
π
πππ
q)
22
)2cos(
2
3
cos)sin(
2
sin
−+
−+
−+
−xxxx
π
π
π
π
r)
−++
+
+
−aaaaa 2
3
tan).tan(
3
5
cos.
3
2
tan.
3
sin
π
π
πππ
s)
)5,3tan()6cot(
)4tan()5,5cot(
ππ
ππ
−−−
−+−
ba
ba
t)
oooooo 700tan.400tan.260tan.250tan.190tan.50tan
4. Cho A, B, C là ba góc c a tam giác ABC. Ch ng minh:ủ ứ
a)
-cosAC)cos(B ;sin)sin( =+=+ CBA
c)
-cotCB)cot(A ;tan)tan( =+−=+ BCA
b)
2
sin
2
CB
cos ;
2
cos
2
BA
sin AC =
+
=
+
d)
2
tan
2
BA
cot ;
2
cot
2
tan CBCA =
+
=
+
5. Tìm giá tr l n nh t c a hàm s : ị ớ ấ ủ ố
2cossin
cos2
−+
+
=xx
x
y
6. Tìm giá tr nh nh t và l n nh t c a hàm s trong kho ng ị ỏ ấ ớ ấ ủ ố ả
ππ
<<− x
:
4sincos2
3sin2cos
+−
++
=xx
xx
y
.
7. G i a, b, c là các c nh đ i di n v i các góc t ng ng c a tam giác ABC. ọ ạ ố ệ ớ ươ ứ ủ
a) Cho
ACB 222 sin2sinsin =+
. Ch ng minh ứ
o
60A ≤
.
b)
ABCcbaCcBbAa ∆⇒++=++ )coscoscos(2
đ u.ề
c) Ch ng minh: ứ
1sinC.sinA-sinB.sinC-sinA.sinB-Csinsinsin0
<++<
BA
Ph n 2: Các công th c l ng giácầ ứ ượ
I. Công th c c ngứ ộ
A. Ki n th c c n nhế ứ ầ ớ
bababa
abbaba
sinsincoscos)cos()2
cossincossin)sin()1
=±
±=±
ba
ba
ba tantan1
tantan
)tan()3
±
=±
B. Bài t pậ
1. Ch ng minh các công th c sau:ứ ứ
a)
+=
−=+ aaaa 4
sin2
4
cos2sincos
ππ
b)
−=
+=− aaaa 4
sin2
4
cos2sincos
ππ
2. Rút g n các bi u th c:ọ ể ứ
a)
++−
+−
aa
aa
4
sin2sin2
4
cos2cos2
π
π
2K2+ - 2 -

Ph ng trình l ng giácươ ượ NXT - FIT
b)
ooooo 79cos.69cos21cos.11cos10cos ++
c)
bababa tan.tan)cot().tan(tan −−−
3. Ch ng minh trong m i tam giác ABC ta đ u có:ứ ọ ề
a)
tanCtanA.tanB.tanCtanBAtan
=++
b)
1
2
tan.
2
tan
2
tan.
2
tan
2
tan.
2
tan =++ ACCBBA
c)
1cot.cotcot.cotcot.cot
=++
ACCBBA
d)
2
cot.
2
cot.
2
cot
2
cot
2
cot
2
cot CBACBA =++
4. a) Cho
4
π
=−ba
, ch ng minh: ứ
a
b
btan
tan1
tan1 =
−
+
và
b
a
atan
tan1
tan1 −=
+
−
.
b) Cho
4
π
=+ ba
, ch ng minh: ứ
2)tan1)(tan1( =++ ba
và
2)cot1)(cot1( =−− ba
c) Cho
nya
max
=−
=+
)tan(
)tan(
. Ch ngminh: ứ
ab
ba
yx +
−
=+ 1
)tan(
.
d) Cho
5
2
tan =a
,
7
3
tan =b
)10( va, b <<
. Tìm a + b.
e) Cho
2
1
tan −=a
)
2
(
π
π
<< a
và
3tan
=
b
)
2
0(
π
<< b
. Tìm a + b.
f) Cho
3
2
1tan =a
,
4
1
tan =b
)10( va, b <<
. Tìm a - b.
g) Cho
12
1
tan =a
,
5
2
tan =b
,
3
1
tan =b
. Ch ng minh a + b + c = 45ứo.
5. Tìm giá tr các hàm s l ng giác góc: ị ố ượ
o
15
ho c ặ
12
π
và
o
75
ho c ặ
12
5
π
.
6. Cho
γβα
, ,
tho mãn đi u ki n: ả ề ệ
2
π
γβα
=++
. Tìm giá tr l n nh t c a bi u th c: ị ớ ấ ủ ể ứ
αγγββα
tan.tan1tan.tan1tan.tan1 +++++=A
7. Ch ng minh r ng n u các góc c a tam giác A, B, C tho mãn m t trong các đ ng th c sau thì tamứ ằ ế ủ ả ộ ẳ ứ
giác ABC cân:
a)
)cot(cot
2
1
sinsin
coscos 22
22
22
BA
BA
BA +=
+
+
b)
A
C
Bcos2
sin
sin =
c)
)tantan(
2
tan BbAa
A
ba +=+
d)
BABA 2
tan.tantan2tan =+
II. Công th c nhân đôi nhân ba.ứ
A. Lý thuy t c n nhế ầ ớ
aaa
aaa
a
a
a
aaaaa
aaa
cos3cos43cos
sin4sin33sin
tan1
tan2
2tan
1sco2sin21sincos2cos
cossin22sin
3
3
2
2222
−=
−=
−
=
−=−=−=
=
B. Bài t pậ
1. Rút g n các bi u th c sau: ọ ể ứ
a)
aaaa
aa
sin3coscos3sin
4
sin.
4
sin
−
+
−
ππ
b)
8tan
1
8
tan2
π
π
−
c)
ooo 80cos.40cos.20cos
d)
)sin(coscossin2 22 aaaa −
2K2+ - 3 -

Ph ng trình l ng giácươ ượ NXT - FIT
e)
aaaa 4224 sincossin6cos +−
f)
2
cos
2
sin4cos 222 aa
a−
g)
aa 22 cossin81−
h)
ooo 40cos20cos10cos8
i)
aaaa 3sincos43cossin4 33 +
j)
aa 2sin4sin4 24 +
k)
5
2
cos
5
cos
ππ
l)
oooo 80cos60cos40cos20cos
m)
aaaaaa 32tan3216tan168tan84tan42tan2tan +++++
n)
aa
aa
3coscos
3sinsin
3
3
−
+
o)
aa
aa
3sinsin
3coscos
+
−
2. Ch ng minh: ứ
a)
aaaa 3sin
4
1
3
sin
3
sinsin =
+
−
ππ
. Áp d ng v i ụ ớ
9
π
=a
.
b)
118sin818sin8 23 =+
c)
32
cot
32
tan
16
tan2
8
tan48
ππππ
=+++
d)
572tan36tan 22 =
oo
e)
aaaa 3cos
4
1
3
cos
3
coscos =
+
−
ππ
. Tính:
18
7
cos
18
5
cos
18
cos
πππ
f)
a
aa
a2
3
tan31
tantan3
3tan −
−
=
g)
aaaa 3tan
3
tan
3
tantan =
+
−
ππ
. Ch ng minh: ứ
5210
15
66tan54tan6tan +
−
=
ooo
.
3. a) Cho
)0,(
2
sin >
+
=ba
ba
ab
α
. Tìm
α
2sin
,
α
2cos
,
α
2tan
.
b) Cho
2
1
2
cos a
a
+
=
α
. Tìm
α
2sin
,
α
2cos
,
α
2tan
.
c) Cho
4
5
cossin =+
αα
. Tìm
α
2sin
,
α
2cos
,
α
2tan
.
4. Tìm giá tr nh nh t và l n nh t c a các hàm s sau:ị ỏ ấ ớ ấ ủ ố
a)
−
+= 4
sin
4
sin
ππ
xxy
b)
xxy 44 sincos −=
c)
xxy 22 cossin81−=
III. Công th c h b c. Công th c vi t các hàm l ng giác theo ứ ạ ậ ứ ế ượ
2
tan a
t=
.
A. Lý thuy t c n nhế ầ ớ
aa
aa
2
2
sin22cos1
cos22cos1
=−
=+
2
1
2
sin t
t
a+
=
2
2
1
1
cos t
t
a+
−
=
2
1
2
tan t
t
a−
=
B. Bài t pậ
1. Ch ng minh các bi u th c sau:ứ ể ứ
a)
2
tan
2sinsin2
2sinsin2 2a
aa
aa =
+
−
b)
−=
++
+− a
aa
aa
4
tan
2cos2sin1
2cos2sin1
π
c)
2
cos4)cos(cos)sin(sin 222 ba
baba +
=+++
d)
a
aa cot2
2
cot
2
tan −=
e)
−=
−
+
24
cot
sin1
sin1 2a
a
a
π
f)
( )( )
1223'307tan −−=
o
g)
2
cos2)cos(coscos)sin(sinsin 2ba
baabaa −
=+++
2K2+ - 4 -
Ph ng trình l ng giácươ ượ NXT - FIT
h)
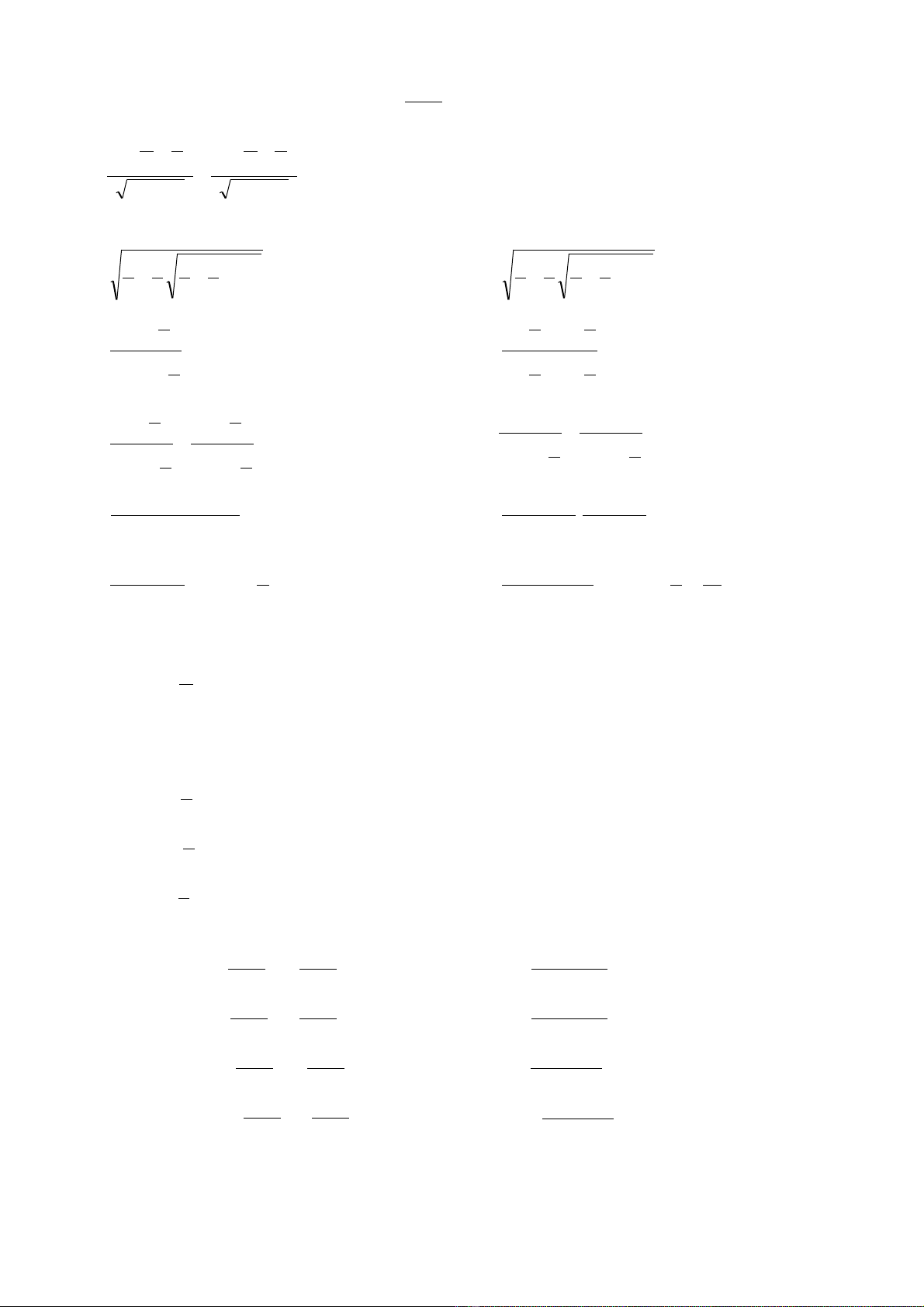
2
sin4)cos(cos)sin(sin 222 ba
baba −
=−+−
i)
a
a
a
a
sin1
24
sin
sin1
24
sin
+
−
−
−
+
ππ
)0(
π
<< a
2. Rút g n các bi u th c sau:ọ ể ứ
a)
α
cos
2
1
2
1
2
1
2
1++
)0(
πα
≤<
b)
α
cos
2
1
2
1
2
1
2
1+−
)0(
πα
≤<
c)
2
cot1
2
cot2
2a
a
+
d)
4
tan
4
cot
2
tan
2
cot
aa
aa
+
−
e)
2
tan1
2
tan
2
tan1
2
tan
a
a
a
a
−
+
+
f)
2
tan1
1
2
tan1
1
aa +
−
−
g)
αα
αα
sin2sin
2coscos1
−
+−
h)
α
α
α
α
cos1
cos
.
2cos1
2sin
++
3. Tìm giá tr bi u th cị ể ứ
a)
a
a
cos23
sin
−
bi t ế
2
2
tan =
a
b)
aa
aa
sintan
sintan
−
+
Bi t ế
15
2
2
tan =
a
4. Tìm giá tr l n nh t và nh nh t c a hàm s :ị ớ ấ ỏ ấ ủ ố
a)
xxy
2
sin2cos2 +=
b)
xxy 2cossin2 2−=
c)
22 )cos(sin
4
sin xxxy −+
−=
π
IV. Công th c bi n đ i t ng và tíchứ ế ổ ổ
A. Lý thuy t c n nhế ầ ớ
1. Công th c bi n đ i tích thành t ngứ ế ổ ổ
[ ]
[ ]
[ ]
)cos()cos(
2
1
sinsin
)cos()cos(
2
1
coscos
)sin()sin(
2
1
cossin
bababa
bababa
bababa
+−−=
−++=
−++=
2. Công th c bi n đ i t ng thành tíchứ ế ổ ổ
2
sin.
2
sin2coscos
2
cos.
2
cos2coscos
2
sin.
2
cos2sinsin
2
cos.
2
sin2sinsin
baba
ba
baba
ba
baba
ba
baba
ba
−+
−=−
−+
=+
−+
=−
−+
=+
ba
ba
ba
ba
ba
ba
ba
ba
ba
ba
ba
ba
sinsin
)sin(
cotcot
sinsin
)sin(
cotcot
coscos
)sin(
tantan
coscos
)sin(
tantan
−
−=−
+
=+
−
=−
+
=+
B. Bài t pậ
1. Rút g n bi u th cọ ế ứ
2K2+ - 5 -


























