
Chuyeân ñeà: Moät soá caùch chöùng minh ñònh lí Pytago Toå: Toaùn
−
−−
−
Vaät lyù
Gvth: Ngoâ Chí Trung Trang 1
Chuyeân ñeà: Moät soá caùch chöùng minh ñònh lí Pytago.
−−−−
PHAÀN I: MÔÛ ÑAÀU.
Ñònh lí Pytago laø moät ñònh lí tuyeät ñeïp cuûa toaùn hoïc. Con ngöôøi ñaõ phaùt hieän
vaø chöùng minh ñöôïc noù caùch nay nhieàu nghìn naêm, töø khi toaùn hoïc vöøa môùi hình
thaønh. Veà caùch chöùng minh ñònh lí Pytago thì coù ñeán haøng trieäu caùch. Caùch coå xöa
nhaát thuoäc veà Pytago. Caùch chöùng minh naøy ñöôïc ghi laïi trong taùc phaåm kinh ñieån
veà hình hoïc “Eleùments” cuûa Euclide khoaûng naêm 300 TCN, song song ñoù, caùch
chöùng minh khaùc cuõng ñöôïc tìm thaáy trong moät taøi lieäu veà toaùn cuûa Trung Quoác
vaøo khoaûng naêm 500 ñeán naêm 200 TCN. Veà sau caùc nhaø toaùn hoïc ñaõ khoâng ngöøng
ñöa ra nhieàu caùch chöùng minh khaùc.
Ñeå chöùng minh ñònh lí Pytago khoâng khoù. Trong chöông trình hình hoïc 7 ñaõ
trình baøy caùch chöùng minh döïa vaøo vieäc ñaët caùc tam giaùc vuoâng coù caïnh a, b, c
vaøo hình vuoâng coù caïnh laø a + b. Caùch naøy giuùp hoïc sinh deõ daøng chöùng minh
ñöôïc ñònh lí Pytago. Ngoaøi ra coøn nhieàu caùch khaùc cuõng döïa vaøo gheùp hình nhöng
theo caùch gheùp khaùc, hoaëc öùng duïng caùc tính chaát dieän tích cuûa ña giaùc, öùng duïng
tam giaùc ñoàng daïng, heä thöùc löôïng trong tam giaùc vuoâng, …
Trong chuyeân ñeà nhoû naøy, toâi xin giôùi thieäu ñeán quyù thaày coâ moät soá caùch
chöùng minh ñònh lí Pytago maø toâi hoaëc tìm ra ñöôïc hoaëc söu taàm ñöôïc, tuy soá caùch
chöùng minh coøn ít raát nhieàu so vôùi soá caùch maø con ngöôøi ñaõ bieát nhöng vôùi soá caùch
chöùng minh naøy cuõng ñoái vôùi toâi cuõng laø moät gia taøi kha khaù. Hy voïng chuyeân ñeà
seõ ñem ñeán cho quyù thaày coâ nhieàu ñieàu thuù vò, töø ñoù vaän duïng vaøo baøi giaûng cuûa
mình nhaèm taêng höùng thuù hoïc taäp moân toaùn cho hoïc sinh.
Chuyeân ñeà: Moät soá caùch chöùng minh ñònh lí Pytago Toå: Toaùn
−
−−
−
Vaät lyù
Gvth: Ngoâ Chí Trung Trang 2
PHAÀN II: NOÄI DUNG.
−−−−
I. Vaøi neùt lòch söû cuûa ñònh lí Pytago.
Trong toaùn hoïc, ñònh lyù Pytago (coøn goïi laø ñònh lyù Pythagore theo tieáng
Phaùp hay ñònh lyù Pythagorastes theo tieáng Anh) laø moät lieân heä trong hình hoïc
phaúng giöõa ba caïnh tam giaùc cuûa moät tam giaùc vuoâng. Ñònh lyù naøy ñöôïc ñaët teân
theo nhaø vaät lí hoïc vaø nhaø toaùn hoïc Hy Laïp Pytago soáng vaøo theá kyû 6 TCN.
Hai caùch chöùng minh coå nhaát cuûa ñònh lyù Pytago ñöôïc cho laø naèm trong
quyeån Chu Beã toaùn kinh (Trung Quoác) khoaûng naêm 500 ñeán 200 TCN vaø
Eleùments cuûa Euclide khoaûng naêm 300 TCN.
Söï lieân heä giöõa caùc caïnh cuûa moät tam giaùc vuoâng ñaõ ñöôïc neâu ra tröôùc
Pytago khoaûng 1200 naêm vaøo thôøi coå Babilon. Nhöng Pytago laø ngöôøi ñaõ chöùng
minh noù vaø môû roäng phaïm vi aùp duïng cuûa noù ñeå giaûi nhieàu baøi toaùn veà lí thuyeát
vaø thöïc tieãn. Ñònh lí Pytago laø chìa khoùa ñeå xaây döïng nhieàu ñònh lí khaùc trong hình
hoïc.
Trong taùc phaåm Eleùments, Euclide trình baøy ñònh lí Pytago nhö sau:
“Trong moät tam giaùc vuoâng, toång dieän tích hai hình vuoâng döïng treân hai
caïnh goùc vuoâng baèng dieän tích hình vuoâng döïng treân caïnh huyeàn”.
Veà sau, ngöôøi ta nhaän thaáy dieän tích hình vuoâng baèng bình phöông caïnh cuûa
noù neân phaùt bieåu laïi: “Trong moät tam giaùc vuoâng, bình phöông caïnh huyeàn baèng
toång caùc bình phöông cuûa hai caïnh goùc vuoâng” nhö chuùng ta ñaõ bieát ngaøy nay.
c
a
b
Chuyeân ñeà: Moät soá caùch chöùng minh ñònh lí Pytago Toå: Toaùn
−
−−
−
Vaät lyù
Gvth: Ngoâ Chí Trung Trang 3
II. Moät soá caùch chöùng minh.
Trong phaàn naøy, toâi xin giôùi thieäu moät soá caùch chöùng minh do toâi söu taàm
ñöôïc, vieäc trình baøy coù theå khoâng theo thöù töï thôøi gian maø caùch chöùng minh ñöôïc
tìm ra. Xin quyù thaày coâ thoâng caûm.
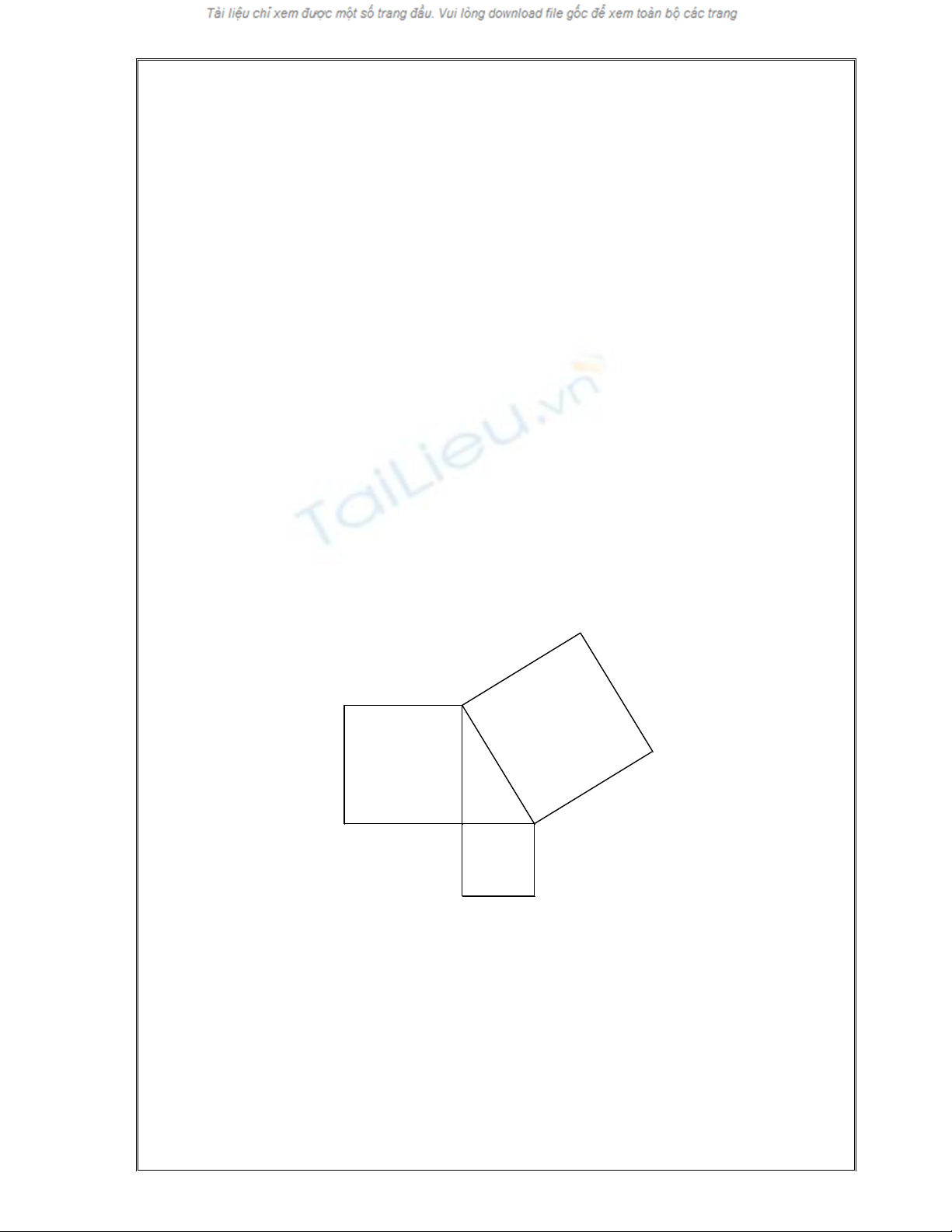
1. Caùch caét vaø gheùp hình thöù nhaát:
Caùch naøy chính laø caùch chuùng ta ñaõ bieát trong saùch giaùo khoa toaùn 7.
Vì hai hình vuoâng treân coù dieän tích baèng nhau neân phaàn dieän tích phaàn
khoâng bò caùc tam giaùc vuoâng che khuaát baèng nhau. Töø ñoù suy ra c
2
= a
2
+ b
2
.
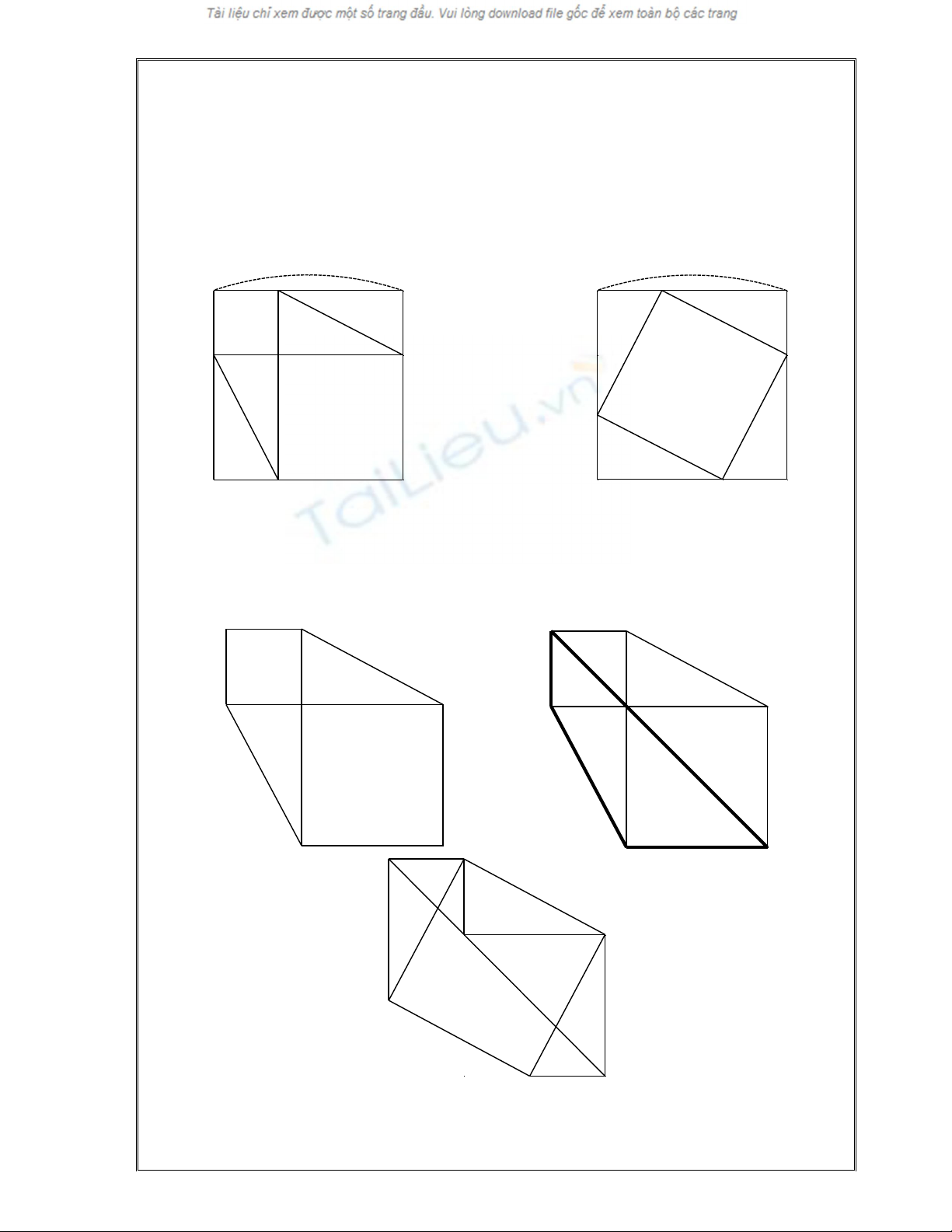
2. Caùch caét gheùp hình thöù hai:
Caùch naøy do Leonardo da Vinci tìm ra.
Laät ngöôïc ña giaùc ñöôïc toâ ñaäm, ta deã daøng nhaän thaáy ña giaùc môùi bao goàm
hai tam giaùc vuoâng ban ñaàu vaø moät hình vuoâng coù caïnh baèng c, töø ñoù suy ra ñöôïc
c
2
= a
2
+ b
2
.
a+b
a
b
a
b
2
2
c
a+b
a
b
2
c
c
c
a
b
c
a
b
c
b
a


























