Chuyên đề nghiên cứu sinh: Ứng dụng lý thuyết matrận-R tính toán tiết diện bắt bức xạ nơtron trong vùng năng lượng cộng hưởng phân giải được

Chia sẻ: Minh Van Thuan | Ngày: | Loại File: PDF | Số trang:27

Thêm vào BST

Báo xấu

70
lượt xem 5
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Chuyên đề nghiên cứu sinh: Ứng dụng lý thuyết matrận-R tính toán tiết diện bắt bức xạ nơtron trong vùng năng lượng cộng hưởng phân giải được trình bày lý thuyết ma trận-R; phương pháp gần đúng Reich-Moore; hiệu chính mở rộng đỉnh Doppler; phát triển chương trình tính toán CrossComp; mô tả chương trình CrossComp;...

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Chuyên đề nghiên cứu sinh: Ứng dụng lý thuyết matrận-R tính toán tiết diện bắt bức xạ nơtron trong vùng năng lượng cộng hưởng phân giải được

BỘ GIÁO DỤC VÀ ĐÀO TẠO BỘ KHOA HỌC VÀ CÔNG NGHỆ VIỆN NĂNG LƯỢNG NGUYÊN TỬ VIỆT NAM ___________________ PHẠM NGỌC SƠN ỨNG DỤNG LÝ THUYẾT MATRẬN-R TÍNH TOÁN TIẾT DIỆN BẮT BỨC XẠ NƠTRON TRONG VÙNG NĂNG LƯỢNG CỘNG HƯỞNG PHÂN GIẢI ĐƯỢC CHUYÊN ĐỀ NGHIÊN CỨU SINH NGƯỜI HƯỚNG DẪN KHOA HỌC: 1. PGS. TS. VƯƠNG HỮU TẤN 2. TS. MAI XUÂN TRUNG ĐÀ LẠT, THÁNG 12/2012 0
MỤC LỤC trang TÓM TẮT 2 I. ĐẶT VẤN ĐỀ 3 II. PHƯƠNG PHÁP NGHIÊN CỨU 5 2.1. Lý thuyết ma trận-R 5 2.2. Phương pháp gần đúng Reich-Moore 9 2.3. Hiệu chính mở rộng đỉnh Doppler 11 2.4. Phát triển chương trình tính toán CrossComp 12 2.4.1. Mô tả chương trình CrossComp 12 2.4.2. Định dạng file input các tham số và file output 15 2.4.3. Các giá trị tổ hợp spin được sử dụng trong chương trình 17 2.4.4. Kiểm tra, hiệu chỉnh và hiệu lực hoá chương trình CrossComp 19 III. KẾT QUẢ VÀ THẢO LUẬN 21 IV. KẾT LUẬN 25 TÀI LIỆU THAM KHẢO 26 1
TÓM TẮT Lý thuyết ma trận-R đã được áp dụng để phát triển chương trình tính toán số liệu tiết diện bắt bức xạ nơtron và phân tích các tham số cộng hưởng trong vùng năng lượng cộng hưởng phân giải được. Chương trình tính toán này đã được phát triển bằng mã nguồn VC++6.0 và được gọi là chương trình “CrossComp”. Các mô hình lý thuyết được sử dụng trong CrossComp là: mô hình gần đúng đa mức Reich-Moore, mô hình Free Gas Model tính toán hiệu ứng mở rộng đỉnh Doppler. Chương trình CrossComp đã được kiểm tra so sánh với số liệu đánh giá trong thư viện số liệu hạt nhân Jendl3.3. và các kết quả so sánh cho thấy có sự phù hợp tốt khi sử dụng các dữ liệu đầu vào trong cùng một file cơ sở dữ liệu. Như là một kết quả minh họa, chương trình CrossComp đã được áp dụng để tính toán số liệu tiết diện bắt bức xạ nơtron của hạt nhân La-139 trong khoảng năng lượng từ 10eV đến 8keV trên cơ sở các số liệu thực nghiệm mới nhất về tham số cộng hưởng của hạt nhân này. 2
I. ĐẶT VẤN ĐỀ Quá trình phản ứng bắt bức xạ nơtron đã quan sát được bằng thực nghiệm đối với hầu hết các hạt nhân và có tốc độ phản ứng chiếm chủ yếu trong vùng năng lượng nơtron nhiệt và năng lượng cộng hưởng. Phản ứng bắt bức xạ diễn ra khi một hạt nhân bia (Z, A) hấp thu một nơtron tạo thành hạt nhân hợp phần (Z, A+1) ở trạng thái kích thích trong khoảng năng lượng từ 4 đến 10MeV, năng lượng này bằng tổng động năng của hạt nơtron tới và năng lượng hụt khối của hệ trước và sau khi phản ứng. Khi năng lượng của hệ hạt nhân hợp phần bằng năng lượng của trạng thái kích thích (Eλ) thì một cộng hưởng phản ứng sẽ được quan sát trên đường cong tiết diện bắt bức xạ nơtron của hạt nhân bia. Thời gian sóng của trạng thái kích thích của hạt nhân hợp phần là rất ngắn khoảng 10-14s và phân rã qua các trạng thái có năng lượng thấp hơn về mức cơ bản theo đó các bức xạ sóng điện từ (tia gamma) được phát ra. Hạt nhân ở trạng thái cơ bản có thể bền hoặc không bền đối với phân rã β hoặc α. 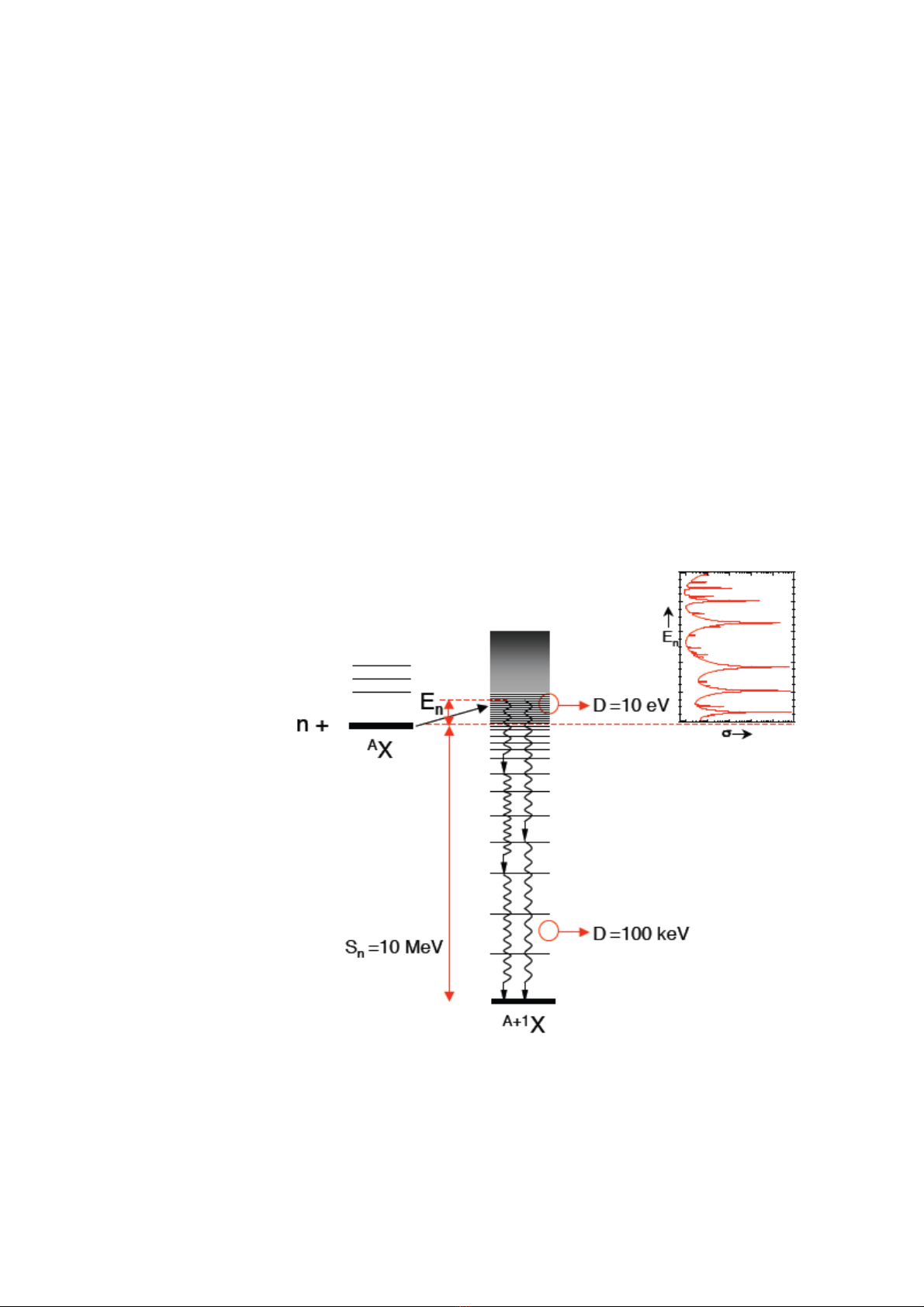Hình 1: Sơ đồ mô tả tổng quát phản ứng bắt bức xạ nơtron Số liệu tiết diện phản ứng hạt nhân là cơ sở quan trọng, cần thiết trong các lĩnh vực nghiên cứu phát triển và ứng dụng của khoa học và công nghệ hạt nhân như: Nghiên 3
cứu vật lý hạt nhân cơ bản, thiết kế và phân tích an toàn lò phản ứng hạt nhân, quản lý, lưu trữ và xử lý nhiên liệu trước và sau khi sử dụng, nghiên cứu vật lý hạt nhân thiên văn, và các ứng dụng khác trong y học, công nghiệp, môi trường,... Các số liệu hạt nhân cơ bản thu nhận được từ đo thực nghiệm hoặc tính toán lý thuyết cần phải được phân tích, hiệu chỉnh và đánh giá trước khi biên dịch thành cơ sở dữ liệu phục vụ cho các nghiên cứu và ứng dụng khác nhau. Cho đến nay, lý thuyết phản ứng hạt nhân vẫn chưa phát triển đến mức có thể tính toán được số liệu tiết diện phản ứng hạt nhân một cách chính xác từ các nguyên lý cơ bản và độc lập với số liệu thực nghiệm[1]. Do đó, các nghiên cứu về đo số liệu thực nghiệm tiết diện phản ứng hạt nhân vẫn đóng một vai trò quan trọng trong sự phát triển chung của lĩnh vực khoa học và công nghệ hạt nhân. Tuy nhiên các số liệu đo thực nghiệm thường không được sử dụng một cách trực tiếp cho các ứng dụng, do các điều kiện thực nghiệm không như là các điều kiện lý tưởng, mà còn chịu các ảnh hưởng như hiệu ứng Doppler, hiệu ứng tự hấp thụ, tán xạ nhiều lần và thường chỉ có thể đo được trong một dải năng lượng giới hạn nhất định phụ thuộc vào thể loại và đặc trưng của từng thiết bị thí nghiệm. Để tạo ra các cơ sở dữ liệu có hiệu quả sử dụng cao, các mô hình tính toán lý thuyết cần được áp dụng để tham số hoá số liệu thực nghiệm và mô tả lại số liệu tiết diện phản ứng từ các tham số này một cách có hệ thống. Các tham số phân tích được từ số liệu thực nghiệm thường là các đặc trưng về cấu trúc cộng hưởng của hạt nhân như năng lượng cộng hưởng, độ rộng mức, độ rộng bức xạ,... và được gọi là các tham số cộng hưởng. Lí thuyết ma trận-R[2,5,6], được giới thiệu vào năm 1947 bởi hai nhà khoa học E.P. Wigner và L. Eisenbud, là một mô hình lý thuyết tán xạ hạt nhân quan trọng được phát triển trong nhiều thập niên qua và có nhiều ứng dụng với độ chính xác cao trong vùng năng lượng cộng hưởng phân giải được. Trong quá trình tính toán và đánh giá số liệu, các chương trình máy tính phát triển trên cơ sở các mô hình lý thuyết, phương pháp gần đúng và kỹ thuật thống kê là rất cần thiết. Để góp phần tạo ra các công cụ tính toán phục vụ cho hoạt động nghiên cứu đánh giá, phân tích và phát triển số liệu hạt nhân, chuyên đề này đã được thực hiện với mục tiêu nghiên cứu ứng dụng lý thuyết ma trận-R (hay còn gọi là lý thuyết tán xạ hạt nhân) để tính toán số liệu tiết diện bắt bức xạ nơtron trong vùng năng lượng cộng hưởng phân giải được. Để đạt được mục tiêu đặt ra, giải pháp thực hiện là trên cơ sở ứng dụng lý thuyết ma trận-R nghiên cứu phát triển một chương trình máy tính bằng 4
mã nguồn VC++6.0 gọi là chương trình CrossComp để phục vụ nội dung tính toán số liệu hạt nhân của luận án nghiên cứu sinh. Chương trình này đã được nghiên cứu phát triển và áp dụng thử nghiệm để tính toán số liệu tiết diện bắt bức xạ nơtron trong vùng năng lượng từ 10eV đến 9keV đối với hạt nhân La-139. Kết quả tính toán đã được so sánh với số liệu trích dẫn từ thư viện JENDL3.3 và ENDF/ B6.8. Các hiệu chính đối với hiệu ứng mở rộng đỉnh Doppler ở các nhiệt độ khác nhau được chương trình thực hiện theo yêu cầu của người sử dụng. Số liệu input là các tham số cộng hưởng và thông tin về số lượng tử spin của hạt nhân bia và hạt nhân hợp phần. II. PHƯƠNG PHÁP NGHIÊN CỨU 2.1. Lý thuyết ma trận-R Lý thuyết ma trận-R[5,6] hay còn gọi là lý thuyết tán xạ hạt nhân do Wigner và Eisenbud giới thiệu vào năm 1947 được các nhà khoa học đánh giá là lý thuyết có cơ sở vật lý tốt và mô tả phù hợp tốt nhất với số liệu thực nghiệm trong vùng năng lượng cộng hưởng phân giải được[4]. Cơ sở phương pháp luận của lý thuyết này là xây dựng một mô hình không gian của hệ tương tác bao gồm hai phần: thành phần bên trong (internal region) mô tả các trạng thái lượng tử của hàm sóng của hạt nhân hợp phần và thành phần bên ngoài (external region) bao gồm các kênh phản ứng khả dĩ tạo nên hạt nhân hợp phần. Sự phân chia cấu hình không gian như vậy được thực hiện bởi sự chọn lựa các điều kiện biên của hạt nhân hợp phần. Mỗi kênh phản ứng tồn tại một giá trị tương ứng của điều kiện biên được chọn đối với một bán kính kênh phản ứng, cho phép chúng ta nhận được một dãy đầy đủ các hàm sóng (wave functions) và được gọi là các cộng hưởng (resonances) của hạt nhân hợp phần. Thành phần cấu hình không gian bên ngoài hàm chứa thông tin cơ bản về lý thuyết tán xạ hạt nhân như: ma trận tán xạ (collision matrix), độ dịch chuyển pha (phase shifts), các hệ số thẩm thấu hạt nhân (penetration factors). Thành phần cấu hình không gian bên trong hàm chứa thông tin về tham số phổ hạt nhân như: mức năng lượng (hay còn gọi là năng lượng cộng hưởng), độ rộng mức, độ rộng rút gọn (reduced widths). 5
Kênh vào Hạt nhân hợp phần Kênh ra Hình 2: Sơ đồ mô tả cấu hình không gian của phản ứng hạt nhân, thành phần bên trong được phân biệt bởi bán kính r = a; l và v là spin quỷ đạo và vận tốc hạt; m, i, z là khối lượng, spin và điện tích của hạt tới; M, I, Z là các đại lượng tương ứng đối với hạt nhân bia. Theo lý thuyết tán xạ, kênh phản ứng được ký hiệu bởi c = (α, l, s, J), - α là cặp hạt và hạt nhân của kênh phản ứng bao gồm các đại lượng khối lượng (m, M), spin (i, I), điện tích (z, Z), - l là mô men quỷ đạo tương đối của cặp hạt (kênh phản ứng), - s là spin của kênh phản ứng : s = i+ I , - J là spin toàn phần của hệ hạt nhân hợp phần: J = s+l Tiết diện phản ứng đối với kênh vào c và kênh ra c’ được mô tả theo ma trận tán xạ như sau[4]: π 2 σ cc ' = g J e 2 iwc δ cc ' −U cc ' δ JJ ' (1.1) k2 2mM 2 k là số sóng của hạt tới : k = (m + M )2 h 2 E , 2 2J + 1 gJ là hệ số thống kê spin : g J = (2i + 1)(2 I + 1) , E là động năng của hạt tới trong hệ toạ độ phòng thí nghiệm Ucc’ là ma trận tán xạ : Ucc’ = ΩcWcc’Ωc’ trong đó : Ωc = ei ( w c −ϕ c ) , wc = 0 khi không tính đến tương tác Coulomb và ϕc là độ dịch pha (shift factor) của tán xạ thế không bao gồm tương tác Coulomb. Ma trận Wcc’ được định nghĩa như sau: Wcc’ = P1/2(I-RL)-1(I-RL*)P-1/2 (1.2) L = (S – B) + iP, R là ma trận-R của hệ tán xạ, P là hệ số thẩm thấu hạt nhân (penetrability), S là hệ số dịch chuyển mức (level shift) và B là hằng số biên tại bề mặt 6
hạt nhân với bán kính ac. Khi không bao gồm tương tác Coulomb, các đại lượng S và P có dạng: S = Sl(ρ) và P = Pl(ρ) với ρ = kac. Bảng 1: Mô tả các biểu thức xác định hệ số thẩm thấu P, độ dịch mức S và độ dịch pha ϕ theo momen quỷ đạo l, bán kính a và số sóng k[1]. l Pl Sl ϕl 0 ρ 0 ρ 1 ρ3/(1 + ρ2) -1 / (1 + ρ2) ρ-tan-1 ρ 2 ρ5/ (9 + 3 ρ2 + ρ4) -(18 + 3 ρ2) / (9 + 3 ρ2 + ρ4) ρ-tan-1[3ρ/ (3 -ρ2)] 3 ρ-tan-1[ρ(15-ρ2) / (15-6 ρ2)] ρ7 / (225 + 45 ρ2) + -(675 + 90 ρ2+ 6 ρ4) / (225 + 45 ρ2 + 6ρ4 + ρ6) 6 ρ4 + ρ6) 4 ρ9/ (11025 + 1575 -(44100 + 4725 ρ2 + 270 ρ4+ 10 ρ6) / ρ-tan-1[ρ(105 - 10 ρ2) / (105 ρ2+ 135ρ4+ 10ρ6+ ρ8 (11025 + 1575 ρ2+ 135 ρ4+ 10 ρ6+ ρ8) – 45 ρ2+ ρ4)] Biểu thức tổng quát của ma trận tán xạ trong công thức (1.1) sẽ xác định được bằng cách khớp các hàm sóng của cấu hình không gian bên trong và bên ngoài tại bán kính ac, đối với hạt nhân hợp phần (thành phần không gian bên trong r < a), phương trình Schrodinger đối với hàm thế ở dạng phức được mô tả như sau: (1.3) Hàm sóng có thể được khai triển thành một tổ hợp của các hàm cơ sở (basic functions): (1.4) và thành phần xuyên tâm của ul(r) được biểu diễn bởi phương trình sau: (1.5) và Ul(r = 0) = 0. Đối với thành phần không gian của kênh phản ứng (thành phần không gian bên ngoài r > a, lực hạt nhân bằng 0, V = W = 0) và hàm sóng có dạng: (1.6) trong đó: Il là hàm sóng vào, Ol là hàm sóng ra và Ul là ma trận tán xạ mô tả xác suất phản ứng từ kênh vào đến kênh ra. Xét trạng thái cộng hưởng với phương trình Schrodinger tương ứng là: HXλ = EλXλ (1.7) 7
Điều kiện biên tương ứng của kênh phản ứng c được xác định bởi biểu thức sau: (rdXλ/dr )/Xλ = bc ; khi r = ac (1.8) Theo định nghĩa của phương trình (1.4) thì hàm sóng toàn phần ψ có thể được khai triển theo các trạng thái cộng hưởng Xλ: (1.9) Cλ là các hệ số khai triển: (1.10) tích phân trong công thức (1.10) lấy trên toàn bộ không gian thể tích của hạt nhân hợp phần. Sử dụng định lý Green sẽ tính được các hệ số khai triển Cλ theo biểu thức dưới đây: (1.11) trong đó: ϕ’ = rdϕ/dr và γλc gọi là biên độ độ rộng rút gọn (reduce width amplitude), (1.12) Như vậy từ công thức (1.8) đến (1.12), khi chúng ta đánh giá hàm sóng tại bề mặt S của hạt nhân hợp phần với bán kính r = ac thì đạo hàm của hàm sóng sẽ xác định được theo biểu thức sau: (1.13) (1.14) Rcc’ được gọi là ma trận-R. Trong vùng không gian bên ngoài (r > ac), hàm sóng toàn phần được biểu diễn theo các hàm sóng của kênh vào và kênh ra theo công thức dưới đây: (1.15) trong đó : Ac và Bc là các hệ số tùy ý, các sóng vào và sóng ra có tính chất đối xứng: (1.16) Theo định nghĩa, ma trận tán xạ có vai trò như là một cầu nối liên kết giữa hàm sóng kênh vào và kênh ra: 8
(1.17) Nếu chúng ta nhân phương trình (1.15) với ψc* và lấy tích phân hai vế trên toàn bộ bề mặt S thì sẽ thu được biểu thức của hàm sóng kênh phản ứng: (1.18) Lấy đạo hàm hàm sóng trong phương trình (1.18) và chia cho chính bản thân hàm sóng đó chúng ta sẽ thu được biểu thức lấy đạo hàm logarit và khớp với phương trình (1.13) chúng ta sẽ thu được biểu thức của ma trận tán xạ theo ma trận-R như sau: (1.19) đặt (kcac)1/2 Oc-1lc’(kc’ac’)-1/2 = ΩcPc1/2Ωc’Pc’-1/2, chúng ta sẽ thu được biểu thức của ma trận tán xạ (1.2). Các công thức tổng quát tính tiết diện phản ứng theo ma trận tán xạ như sau[16]: Tiết diện toàn phần : π σ total = ∑∑∑ g a [δ cc ' − U cc ' ] 2 2 (1.20) c c' J k a Tiết diện tán xạ đàn hồi : π ⎡ 2⎤ σ aa = k 2 ∑ J g J ∑ ⎢1 − 2 Re(U cc ) + ∑ U cc ' ⎥ c ⎣ c' ⎦ (1.21) a Tiết diện tán xạ không đàn hồi: π ∑ g J ∑∑ U cc ' 2 σa reaction = 2 (1.22) ka J c c' Tiết diện phản ứng bắt bức xạ: π ⎡ 2⎤ σ capture = 2 ka ∑ J g J ∑ ⎢1 − ∑ U cc ' ⎥ c ⎣ c' ⎦ (1.23) 2.2. Phương pháp gần đúng Reich-Moore Khi xem xét các kênh phản ứng thì kênh phản ứng bắt bức xạ (capture channel) bao gồm các bức xạ gama và hạt nhân với số khối A+1 và có tính chất rất khác biệt so với các kênh phản ứng là các cặp hạt. Điều này dẫn đến ý tưởng xây dựng một biểu thức ma trận-R gần đúng chỉ đối với các kênh là các cặp hạt (ngoại trừ kênh bắt bức xạ). Khi đó tiết diện phản ứng bắt bức xạ sẽ được tính bằng hiệu của tiết diện toàn phần trừ cho tổng của tất cả các kênh phản ứng là cặp hạt. Các điều kiện gần đúng là: có thể xử 9
lý tất cả các kênh bắt bức xạ (captures) như là một đại lượng trung bình, không có hoặc có thể bỏ qua sự ảnh hưởng giữa kênh bắt bức xạ và các kênh khác, có thể bỏ qua sự tương tác giữa các kênh gamma. Biểu thức ma trận-R theo gần đúng Reich-Moore được mô tả như sau[2,16]: (1.24) Trong đó: c, c’ là ký hiệu đối với các kênh là cặp hạt (không phải kênh capture), Γλγ gọi là độ rộng bức xạ tương ứng với kênh capture, γλc gọi là biên độ độ rộng rút gọn và liên hệ với tham số độ rộng kênh theo biểu thức: Γλc = 2γ2λc Pc(E). Viết lại công thức (1.2) đối với ma trận W theo dạng sau: (1.25) đặt ma trận X: (1.26) → W = I +2iX Các công thức tính tiết diện phản ứng theo năng lượng được mô tả như sau[16]: (1.27) (1.28) (1.29) Để minh hoạ, chúng ta áp dụng đối với trường hợp đơn giản là hệ tán xạ chỉ có hai kênh và một mức cộng hưởng, và với một hệ tán xạ như vậy thì hệ số dịch chuyển pha bằng zero và ma trận X trong công thức (1.26) có dạng sau: (1.30) trong đó: D = Eλ – E – iγ2λγ 10
Thay các đại lượng vào và rút gọn chúng ta sẽ thu được biểu thức của ma trận X như sau: (1.31) trong đó: Γ = Γ1 + Γ2 + Γγ. Thay biểu thức (1.31) của ma trận X vào các công thức tiết diện (1.27), (1.28) và (1.29) sẽ thu được dạng tường minh của công thức tính tiết diên phản ứng như sau: (1.32) (1.33) (1.34) trong đó: d = |Eλ – E – iΓ/2|2= (Eλ – E)2 + (Γ/2)2 2.3. Hiệu chính mở rộng đỉnh Doppler Hiệu ứng Doppler là sự mở rộng ở các đỉnh cộng hưởng trong đường cong tiết diện phản ứng nhưng diện tích của đỉnh cộng hưởng thì không đổi. Nguyên nhân của hiệu ứng này là do sự chuyển động nhiệt của các hạt nhân trong bia mẫu. Để mô tả chính xác thông tin về tiết diện phản ứng trong vùng cộng hưởng tại một điều kiện nhiệt độ nào đó, hoặc phân tích các tham số thực nghiệm đo tại một điều kiện nhiệt độ thực tế của môi trường thí nghiệm, bắt buộc chúng ta phải đưa vào các hàm tính toán hiệu 11
chính cho hiệu ứng này. Hoặc có thể tính toán số liệu tương ứng với các nhiệt độ khác nhau tuỳ theo yêu cầu ứng dụng của người sử dụng. Mô hình tính toán được sử dụng phổ biến hiện nay trong hiệu chính mở rộng đỉnh Doppler là mô hình khí tự do (Free-Gas Model of Doppler Broadening), được mô tả theo công thức sau[9]: (3.1) trong đó: σD(E) là tiết diện phản ứng đã được mở rộng Doppler, σ(E) là tiết diện phản ứng chưa được mở rộng Doppler và đại lượng ΔD gọi là độ rộng Doppler. 4mEkT ΔD = , (3.2) M trong đó: m là khối lượng hạt tới (nơtron), M là khối lượng của hạt nhân bia, k là hằng số Boltzaman và T là nhiệt độ với đơn vị là oK. Công thức (3.1) có thể được viết lại theo vận tốc của hạt tới v (v = √E): (3.3) mkT trong đó: v’ = √E’ và u = . M 2.4. Phát triển chương trình tính toán CrossComp Từ các mô hình lý thuyết đã nghiên cứu và tìm hiểu ở trên đây, vấn đề đặt ra là triển khai thực hiện các tính toán và phân tích số liệu một cách chính xác. Một chương trình máy tính đã được nghiên cứu phát triển gọi là “CrossComp” phục vụ tính toán và đánh giá số liệu tiết diện phản ứng bắt bức xạ nơtron trong vùng năng lượng của các cộng hưởng tách rời nhau hay còn gọi là các cộng hưởng phân giải được. 2.4.1. Mô tả chương trình CrossComp Chương trình tính toán CrossComp đã được nghiên cứu phát triển bằng mã nguồn VC++6.0. Cấu trúc sơ đồ thuật toán của chương trình được mô tả trên Hình 4, bao gồm 10 chương trình con được gọi bởi chương trình chính trong quá trình thực thi các 12
lệnh tính toán. Giao diện window của chương trình được giới thiệu trên Hình 3. Danh sách các hàm và biến đã được phát triển và sử dụng trong chương trình được mô tả trong Bảng 2. Bảng 2: Danh sách các hàm và biến đã được phát triển và sử dụng trong CrossComp Tên hàm, biến Chức năng START Lệnh thi hành chương trình. CrossCal Chương trình con tính toán số liệu tiết diện. CrossFit Chương trình con khớp bình phương tối thiểu, phân tích các tham số cộng hưởng. Factors Tình toán các hệ số: mômen xung lượng, hệ số thẩm thấu, bán kính kênh, hệ số dịch pha,… Sima(E) Tính toán tiết diện phản ứng tại năng lượng E DCross Hiệu ứng Doppler broadening Derivation Xác định đạo hàm riêng theo tham số cộng hưởng SpinGroup Biến lớp cấu trúc các nhóm spin Er Năng lượng cộng hưởng Gn Vector độ rộng cộng hưởng nơtron Gg Vector độ rộng bức xạ gamma Gt Vector độ rộng toàn phần CapCS Mảng số liệu tiết diện bắt bức xạ nơtron En Mảng dữ liệu về các điểm năng lượng PShift Phase shift- độ dịch pha Lshift Level shift-biến số mang thông tin về độ dịch mức Penetr Độ thẩm thấu hạt nhân. 13
Hình 3: Giao diện window của chương trình CrossComp 14
CrossComp START Tính toán tiết diện Phân tích tham số cộng hưởng CrossCal CrossFit Đọc file số liệu input Đọc file số liệu thực (Iparametors.dat) nghiệm (Expdata.dat) Tính các hệ số: φl, Sl, Pl Factors Đạo hàm (Derivation) Tính tiêt diện tại Ei Sima(Ei) OutPut (Oparameters.dat) Doppler Broadening DCross Data Plot & Comparision Output OutData.dat Hình 4: Sơ đồ thuật toán của chương trình CrossComp. 2.4.2. Định dạng file input và file output File số liệu input cung cấp cho chương trình các thông tin về các tham số cộng hưởng, là file số liệu đầu vào quan trọng nhất và phải được chuẩn bị bởi người sử dụng theo một định dạng (format) quy định sẳn của chương trình, nhờ đó mà chương trình luôn đọc đúng thông tin về số liệu đầu vào trước khi thi hành chu trình tính toán cho từng bài toán cụ thể. Đối với chương trình CrossComp, kiểu định dạng của file input được xây dựng theo cấu trúc của các nhóm spin J, điều này tạo ra sự phù hợp một cách tương đối đồng dạng với chu trình vòng lặp tính tiết diện phản ứng theo thứ tự các 15
kênh spin (spin channel) hay còn gọi là nhóm spin. Mỗi nhóm spin bao gồm một số hữu hạn các mức hay trạng thái cộng hưởng. Cấu trúc định dạng file input được mô tả như sau đây và một ví dụ điển hình được trình bày trên Bảng 3. File số liệu output của chương trình được tổ chức thành dạng bảng như trong Bảng 4. -------------------------------------------------------------- NS (Số nhóm spin) 1 (Nhóm spin 1) Nr1 (Số trạng thái cộng hưởng ứng với J1) 1 J1 Er Gt Gn Gg l 2 J1 Er Gt Gn Gg l . . Nr1 J1 Er Gt Gn Gg l 2 (nhóm spin thứ 2) Nr2 (số các trạng thái cộng hưởng ứng với J2) 1 J2 Er Gt Gn Gg l 2 J2 Er Gt Gn Gg l . . . Nr2 J2 Er Gt Gn Gg l . . . NS (nhóm spin thứ NS) NrNS (số các trạng thái cộng hưởng ứng với JNS) 1 JNS Er Gt Gn Gg l 2 JNS Er Gt Gn Gg l . . NrNS JNS Er Gt Gn Gg l ------------------------------------------------------------- Bảng 3: Một file các tham số input của hạt nhân La-139 (trích dẫn từ Jendl3.3) Input Resonance Parameter file of La-139 Index J Er(eV) Gt(eV) Gn(eV) Gg(eV) l 2 1 21 1 3 72.3 0.0883332 0.0345143 0.0538189 0 2 3 962.9 0.0494302 0.0198857 0.0295445 0 3 3 1179.4 2.162553 2.112 0.0505532 0 4 3 2115.9 3.957646 3.88571 0.0719361 0 5 3 2380.9 0.127033 0.0777143 0.0493187 0 6 3 2666 0.1175403 0.08263 0.0349103 0 7 3 2857 0.5107603 0.4526 0.0581603 0 8 3 3288 2.404129 2.354 0.0501287 0 9 3 4361 5.771009 5.714 0.0570091 0 10 3 4818 0.2296908 0.1749 0.0547908 0 11 3 5353 1.446068 1.371 0.0750678 0 12 3 6463 4.839152 4.777 0.0621525 0 13 3 6560 1.777632 1.714 0.063632 0 14 3 6991 1.479591 1.371 0.108591 0 15 3 7100 0.3704702 0.3086 0.0618702 0 16 3 7448 0.3864925 0.2971 0.0893925 0 17 3 7466 2.359458 2.286 0.073458 0 18 3 8363 0.5825165 0.5223 0.0602165 0 19 3 8519.5 5.796152 5.714 0.082152 0 16
20 3 8672 0.9034862 0.8514 0.0520862 0 21 3 8915 8.477789 8.411 0.0667887 0 2 51 1 4 617.2 0.0572007 0.0264889 0.0307118 0 2 4 875.4 0.0435391 0.0204444 0.0230947 0 3 4 2151.6 0.9174156 0.856889 0.0605266 0 4 4 2464.6 0.9581284 0.910222 0.0479064 0 5 4 2998 10.25832 10.22 0.0383191 0 6 4 3485 12.82103 12.8 0.0210313 0 7 4 3729 0.270665 0.1627 0.107965 0 8 4 3749 4.613328 4.569 0.0443283 0 9 4 4650 3.202486 3.156 0.046486 0 10 4 5529 0.2576075 0.2222 0.0354075 0 11 4 5833 1.116954 1.067 0.0499541 0 12 4 5979 0.5496754 0.5084 0.0412754 0 13 4 6864 3.292432 3.244 0.0484324 0 14 4 7137 2.365712 2.311 0.0547117 0 15 4 7550 0.263781 0.2311 0.032681 0 36 4 17973 1.668 1.618 0.05 0 37 4 19480 2.974 2.924 0.05 0 38 4 19649 2.041 1.991 0.05 0 39 4 20465 7.428 7.378 0.05 0 40 4 21017 17.83 17.78 0.05 0 41 4 21409 15.69 15.64 0.05 0 42 4 21505 3.961 3.911 0.05 0 43 4 21745 4.139 4.089 0.05 0 44 4 22281 5.357 5.307 0.05 0 45 4 23269 8.183 8.133 0.05 0 46 4 23514 9.028 8.978 0.05 0 47 4 24666 25.21 25.16 0.05 0 48 4 24826 1.454 1.404 0.05 0 49 4 25509 10.27 10.22 0.05 0 ---------------------------------------------------------------------- Bảng 4: Định dạng file số liệu output ------------------------------------------------------------------------------------ E(eV) σ(E) barn 0.0253 653.500 0.0274417 601.934 0.0297445 554.854 0.0322175 511.861 0.0348699 472.583 0.0378217 435.400 0.0409956 401.436 0.0444041 370.405 0.0480598 342.044 0.0521281 315.184 0.0565026 290.640 ------------------------------------------------------------------------------ 2.4.3. Các giá trị tổ hợp spin được sử dụng trong chương trình Trong các chương trình tính toán và đánh giá số liệu hạt nhân, yêu cầu phải thiết lập các nhóm spin (kênh spin) một cách chính xác và đầy đủ trên cơ sở quy tắc tổ hợp lượng tử của các véctor spin. Như đã đề cập đến trong phần lý thuyết tán xạ, kênh phản ứng được ký hiệu bởi c = (α, l, s, J), Trong đó: - α là cặp hạt và hạt nhân của kênh phản ứng bao gồm các đại lượng khối lượng (m, M), spin (i, I), điện tích (z, Z), 17
- l là mô men quỷ đạo tương đối của cặp hạt, - s là spin của kênh phản ứng :s = i + I , - J là spin toàn phần của hệ hạt nhân hợp phần: J = s + l Sử dụng quy tắc tổ hợp lượng tử véctor spin sau đây chúng ta sẽ xác định được giá trị khả dĩ của các kênh spin s và J như sau: I −i ≤ s ≤ I +i ; l−s ≤ J ≤l+s Bảng 5: Các giá trị khả dĩ của tổ hợp của hai đại lượng véctor 0 1/2 1 3/2 2 5/2 3 7/2 4 9/2 0 0 1/2 1/2 0, 1 3/2 3/2 1/2 1/2, 0, 3/2, 1, 5/2 2, 3 2 2 3/2, 1, 1/2, 0, 5/2, 2, 3/2, 1, 3 5/2, 2, 3, 7/2 4, 5 5/2 5/2 2, 3/2, 1, 1/2, 0, 3 5/2, 2, 3/2, 1, 7/2 3, 5/2, 2, 4 7/2, 3, 9/2, 4,5 3 3 5/2, 2, 3/2, 1, 1/2, 0, 7/2 3, 4 5/2, 2, 3/2, 1, 7/2, 3, 5/2, 2, 9/2 4, 7/2, 4, 5 9/2, 5, 11/2 6 7/2 7/2 3, 4 5/2, 2, 3/2, 1, 2, 1/2, 0, 7/2, 3, 5/2, 3, 4, 3/2, 1, 9/2, 4, 7/2, 5, 6 5/2, 2, 5 9/2, 7/2, 3, 11/2 9/2, 4, 11/2, 5, 13/2 6, 7 4 4 7/2, 3, 5/2, 2, 3/2, 1, 1/2, 0, 9/2, 4, 7/2, 3, 5/2, 2, 3/2, 1, 5 9/2, 4, 7/2, 3, 5/2, 2, 11/2 5 9/2, 4, 7/2, 3, 11/2, 5, 9/2, 11/2, 4, 13/2 6, 7 13/2, 15/2 5, 6, 7, 8, 9/2 9/2 4, 7/2, 3, 5/2, 2, 3, 3/2, 1, 1/2, 0, 5 9/2, 4, 7/2, 4, 5, 5/2, 2, 3/2, 1, 11/2 5, 9/2, 6, 7 7/2, 3, 5/2, 2, 6 11/2, 9/2, 4, 7/2, 3, 13/2 11/2, 5, 9/2, 4, 13/2, 6, 11/2, 5, 15/2 7, 13/2, 6, 8 15/2, 7, 17/2 8, 9 18
2.4.4. Kiểm tra, hiệu chỉnh và hiệu lực hoá chương trình CrossComp Chương trình CrossComp đã được phát triển (phiên bản đầu tiên) với các chức năng tính toán và cấu trúc chương trình đã được trình bày trong các mục trên đây. Một nội dung quan trọng cần thiết phải thực hiện để bảo đảm độ tin cậy đối với các kết quả tính toán (output) là kiểm tra, thử nghiệm và hiệu lực hoá chương trình trước khi đưa vào sử dụng. Chúng tôi đã tiến hành kiểm tra chương trình bằng cách so sánh số liệu tính toán với các số liệu đã được đánh giá trong thư viện số liệu Jendl3.3[14] đối với đỉnh cộng hưởng 72.3eV và 962.9eV của hạt nhân La-139, trong đó các số liệu input về tham số cộng hưởng của hạt nhân này cũng được trích dẫn từ Jendl3.3[14] và nhiệt độ Doppler là T = 300oK. Các kết quả so sánh và kiểm tra được mô tả trên các Hình 5, 6 và 7 cho thấy rằng kết qủa tính toán bằng chương trình CrossComp có độ tương tự khá tốt so với số liệu đã được đánh giá trong Jendl3.3 và có thể nhận định rằng Chương trình CrossComp đã có thể đưa vào sử dụng được và tiếp tục phát triển trong tương lai. 1.E+04 Resonance at 72.3eV of La--139 1.E+03 CrossComp Tiết diện (n, g) (barn) Jendl3.3 Exp. Data 1.E+02 1.E+01 1.E+00 1.E-01 6.5E+01 7.0E+01 7.5E+01 8.0E+01 Năng lượng (eV) Hình 5: So sánh kết quả tính toán tiết diện phản ứng bắt bức xạ nơtron tại đỉnh cộng hưởng 72.3 eV của hạt nhân La-139 với số liệu đánh giá trong Jendl3.3. 19