
Trung Tâm Luyện Thi CLC STAR http://maths.edu.vn
GV: Lê Quang Điệp Tel: 0974200379–0633755711 54H Bùi Thị Xuân-Đà Lạt. Trang 1
I.Nguyên hàm – Tích phân.
CHUYÊN ĐỀ VII : ĐẠO HÀM.
Công thức đạo hàm cần nhớ:
'
A0
oï nguyeân haø C
'''
u v u v
oï nguyeân ha
'
x1
'''
u.v u .v u.v
'
2
11
xx
''
2
1u
uu
'1
x .x
'''
2
u u .v u.v
vv
'1
ln x ; x 0
x
'
'u
ln u u
'
xx
ee
'
u ' u
e u .e
'
xx
a a ln a.
'
u ' u
a u .a ln a.
'
a
1
log x x ln a
'
'
a
u
log u u ln a
'
s inx cos x
''
s inu u .cos u
'
cosx sin x
''
cosu u .sin u
'
2
1
tanx cos x
'
'
2
u
tanu cos u
'
2
1
cotx sin x
'
'
2
u
cotu sin u
''
kx k x k
''
ku k u
'' 1
kx k x k. .x
'' '
1
ku k u k. .u . u
''1
sin u u . .sin u.cosu
''1
cos u u . .cos u.sin u
CHUYÊN ĐỀ VIII : NGUYÊN HÀM – TÍCH PHÂN.
I.Công thức nguyên hàm cần nhớ :
1
x
x dx C
1
1
ax b
ax b dx C
a1
1dx ln x C
x
11
dx ln ax b C
ax b a

Trung Tâm Luyện Thi CLC STAR http://maths.edu.vn
GV: Lê Quang Điệp Tel: 0974200379–0633755711 54H Bùi Thị Xuân-Đà Lạt. Trang 2
x
xa
a dx C
ln a
kx b
kx b a
a dx C
k.ln a
xx
e dx e C
ax b ax b
1
e dx e C
a
sinxdx cosx C
1
sin ax b dx cos ax b C
a
cosxdx sinx C
1
cos ax b dx sin ax b C
a
2
1dx t anx C
cos x
2
11
dx t an ax b C
a
cos ax b
2
1dx co t x C
sin x
2
11
dx co t ax b C
a
sin ax b
tan xdx ln cos x C
1
tan ax b dx ln cos ax b C
a
cotxdx ln sin x C
1
cot ax b dx ln sin ax b C
a
adx ax C
'
fx
dx ln f x C
fx
1dx 2 x C
x
22
1 1 x a
dx ln C
2a x a
xa
II.Phương Pháp tính tích Phân.
1.Phương pháp tích phân từng phần.
b
a
I f x .g x dx.
đặt
'
du f x dx
u f x
dv g x dx v g x dx G x
bb
b
b'
aa
aa
I u.v vdu f x .G x G x .f x dx
Dạng 1:
b
a
I f x .ln g x dx
đặt
u ln g x
dv f x
Dạng 2:
b
a
I f x sin g x dx
đặt
u f x
dv sin g x dx
b
a
I f x cos g x dx
đặt
u f x
dv cos g x dx
Dạng 3:
b
gx
a
I f x .e dx
đặt
gx
u f x
dv e dx
Trung Tâm Luyện Thi CLC STAR http://maths.edu.vn
GV: Lê Quang Điệp Tel: 0974200379–0633755711 54H Bùi Thị Xuân-Đà Lạt. Trang 3
Dạng 4:
b
gx
a
I sin f x .e dx
đặt
gx
u sin f x
dv e dx
b
gx
a
I cos f x .e dx
đặt
gx
u cos f x
dv e dx
Riêng dạng này ta nên tính tích phân 2 lần như vậy để được trở lại như đề rồi
I
.
2.Phương pháp đổi biến số.
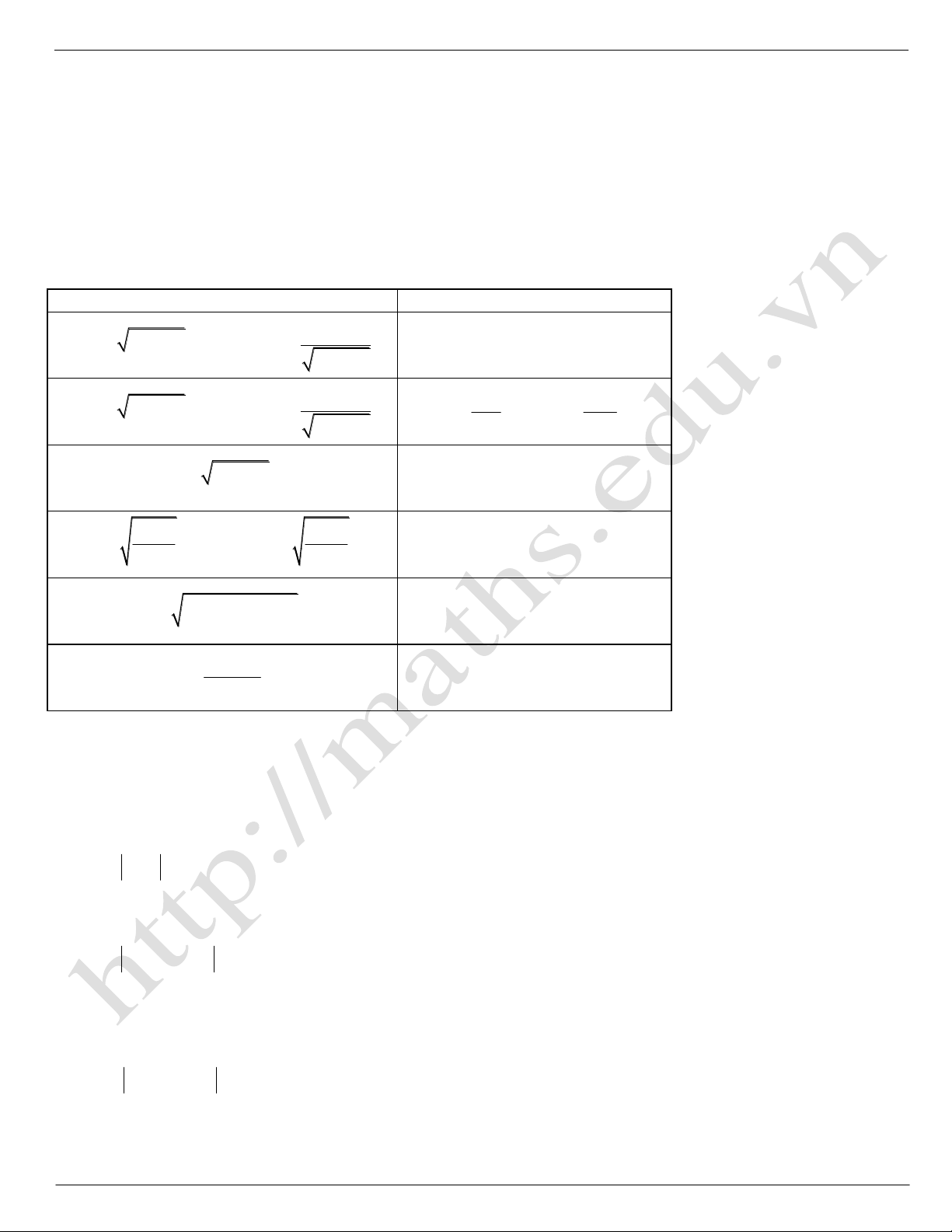
Các dạng
Cách đặt
2
1
b
22
b
I a x dx
hoặc
2
1
b
22
b
dx
I
ax
Đặt
x a sin t
hoặc
x a cos t
2
1
b
22
b
I x a dx
hoặc
2
1
b
22
b
dx
I
xa
Đặt
sint
a
x
hoặc
a
xcost
;
2
1
b
22
b
I a x dx
Đặt
x a tan t
hoặc
x a cott
2
1
b
b
ax
I dx
ax
hoặc
2
1
b
b
ax
I dx
ax
Đặt
x a cos2t
2
1
b
b
I x a b x dx
Đặt
2
x a b a sin t
2
1
b
22
b
1
I dx
ax
Đặt
x a tan t
III.Ứng dụng tích phân.
1. Diện tích giới hạn hình phẳng.
Dạng 1. Hình phẳng giới hạn bởi : Hàm số
y f x C
,trục hoành
y0
và hai đường thẳng
x a,x b
.Giải phương trình hoành độ giao điểm của
C
và
12
ox f x 0 x ,x ...
b
a
S f x dx
có thể bỏ dấu trị tuyệt đối bằng cách :
1
1
xb
ax
S f x dx f x dx...
hoặc dựa vào đồ thị
Dạng 2. Hình phẳng giới hạn bởi : Hàm số
12
y f x C ; y g x C
và hai đường thẳng
x a,x b
.
b
a
S f x g x dx
có thể bỏ dấu trị tuyệt đối bằng cách dựa vào đồ thị.
Dạng 3. Hình phẳng giới hạn bởi : Hàm số
12
y f x C ;y g x C
Giải phương trình hoành độ giao điểm của
1
C
và
2 1 2 3
C f x g x x ,x ,x ...
3
1
x
x
S f x g x dx
có thể bỏ dấu trị tuyệt đối bằng cách :
3
2
12
x
x
xx
S f x g x dx f x g x dx...
hoặc dựa vào đồ thị.

Trung Tâm Luyện Thi CLC STAR http://maths.edu.vn
GV: Lê Quang Điệp Tel: 0974200379–0633755711 54H Bùi Thị Xuân-Đà Lạt. Trang 4
2. Thể tích vật tròn xoay.
Vật thể tròn xoay giới hạn bởi
y f x C ,y 0
;
x a,x b
xoay quanh
b
2
a
ox V f x dx.
Vật thể tròn xoay giới hạn bởi
x f y C ,x 0
;
y a, y b
xoay quanh
II.Bài Tập.
1.Nguyên hàm.
Baøi 1: Tính caùc nguyeân haøm baèng caùch söû duïng baûng nguyeân haøm
1.
.
154
3
34
dx
x
xx
2.
ax
dx
3.
(3- x2)3dx
4.
xx ee
dx
5.
dx
x
x2
)
1
(
6.
sin2xdx.
7.
x
dx
.
8.
(a + bx)2dx -
(a - bx)2dx.
9.
(1 - sinx)2dx +
(1 + cosx)2dx
10.
.
52 x
dx
11.
dxx.31
3
.
12.
2
2 xx
dx
13.
2
5
)25( x
dx
14.
(sin5x - cos5x)dx.
15.
9
2x
dx
16.
dx
x
x
1
3
17.
xx
dx
5
ln
18.
dx
e
e
x
x
1
2
2
19.
(e2x +5)2e2xdx
20.
cos(3ex +1)exdx
21.
.
cos2dx
x
etgx
Baøi 2 : Tính caùc nguyeân haøm sau (ñoåi bieán soá):
1. (2x - 5)5dx
2. x(1 + x2)4/3dx
3. x2(8 - x3)4 dx
4. sin3xdx
5. cos3xdx
6. sinxcos4xdx
7. cosxsin5xdx
8. sin3x.cos2xdx
9. (esinx - cosx)cosxdx
10.
dxxe x
2
11. cos3xsin2xdx
12.
dx
x
x
ln
13.
dx
x
x2
ln
14.
dx
x
x
ln1
15.
dx
x
x
2
ln1
16.
dx
x
x
sin21
cos
17. x(4-x)3dx
18. x
x52
dx
19.
dx
xx
x
53
32
2
20. x2(x3 - 8)3dx
Baøi 3 : Tính caùc nguyeân haøm sau baèng phöông phaùp töùng phaàn:
1. (1 - 3x)exdx
2. xe2xdx
3. x.e-xdx
4. lnxdx
7. xsinxdx
8. xcosxdx
9. (2x-1)sinxdx
10. (1- 4x)cosxdx
12.
dx
x
x
2
sin
13. (x2 - 4x + 3)exdx
14. exsinxdx
16. xlnxdx
17. xln(x+1)dx
18. xsinx5xdx
19. xcos3xdx

Trung Tâm Luyện Thi CLC STAR http://maths.edu.vn
GV: Lê Quang Điệp Tel: 0974200379–0633755711 54H Bùi Thị Xuân-Đà Lạt. Trang 5
5. x2lnxdx
6. x2ex
11.
dx
x
x
2
cos
15. excosxdx
20. ln(5x+1)dx
2.Tích phân.
Bài 1. ĐH, CĐ Khối A – 2005:
2
0cos31
sin2sin
dx
x
xx
I
KQ:
34
27
Bài 2. ĐH, CĐ Khối B – 2005:
dx
x
xx
I
2
0cos1
cos2sin
KQ:
2ln2 1
Bài 3. ĐH, CĐ Khối D – 2005:
2
0
sin coscos
xdxxeI x
KQ:
e1
4
Bài 4. Tham khảo 2005:
dx
x
x
I
7
0
31
2
KQ:
141
10
Bài 5. Tham khảo 2005:
3
0
2
sin
xtgxdxI
KQ:
3
ln2 8
Bài 6. Tham khảo 2005
4
0
sin cos.
dxxetgxI x
KQ:
1
2
ln 2 e 1
Bài 7. Tham khảo 2005
exdxxI
1
2ln
KQ:
3
21
e
99
Bài 8. CĐ Khối A, B – 2005
dxxxI
1
0
23 3.
KQ:
6 3 8
5
Bài 9. CĐ Xây Dựng Số 3 – 2005
3
1313
3dx
xx
x
I
KQ:
6ln3 8
Bài 10. CĐ GTVT – 2005
dxxxI
1
0
25 1
KQ:
8
105
Bài 11. CĐ Kinh Tế Kỹ Thuật I–2005:
2
0
35sin
xdxeI x
KQ:
3
2
3.e 5
34
Bài 12. CĐ Tài Chính Kế Toán IV–2005:
dxxxI 5
3
0
3.1
KQ:
848
105
Bài 13. CĐ Truyền Hình Khối A – 2005:
4
0
2
2sin1
sin21
dx
x
x
I
KQ:
1ln2
2
Bài 14. CĐSP Tp.HCM – 2005:
0
1
242xx
dx
I
KQ:
3
18


























