Baìi giaíng Cå såí thiãút kãú maïy - Pháön I - Lã Cung - Bäü män Nguyãn lyï Chi tiãút maïy - Khoa Sæ phaûm kyî thuáût 81
CHÆÅNG VIII
TRUYÃÖN ÂÄÜNG ÂAI
8.1. Khaïi niãûm chung
1. Giåïi thiãûu bäü truyãön âai
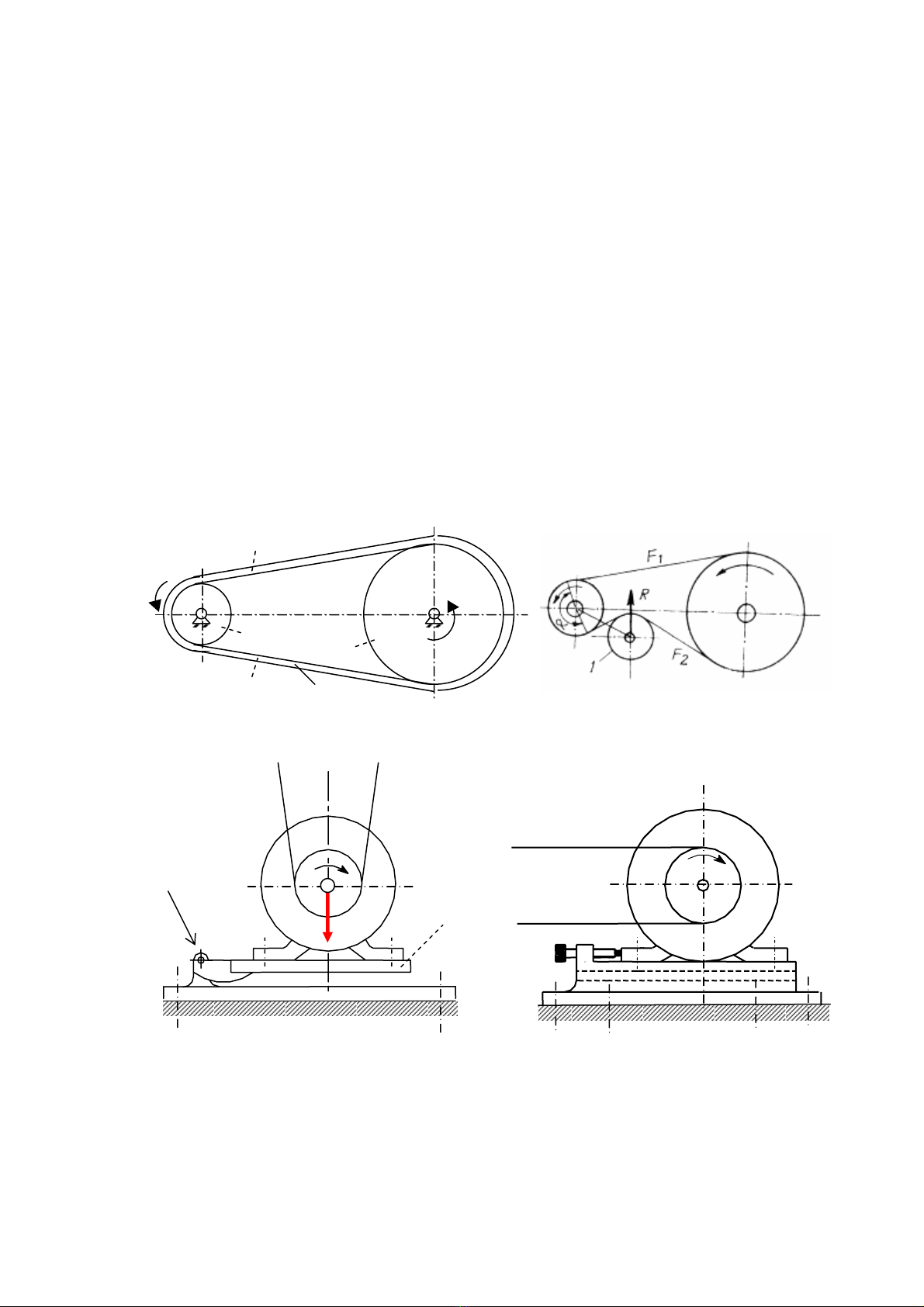
Bäü truyãön âai (hçnh 8.1) thæåìng bao gäöm: baïnh âai dáùn (1), baïnh âai bë dáùn (2) vaì dáy âai
(3) màõc lãn hai baïnh âai. Dáy âai trong bäü truyãön âai laì mäüt kháu mãöm (kháu deío) liãn kãút hai
baïnh âai laûi våïi nhau. Caïc baïnh âai âæåüc näúi våïi giaï bàòng khåïp quay.
Chuyãøn âäüng quay vaì taíi troüng âæåüc truyãön tæì baïnh dáùn sang baïnh bë dáùn nhåì læûc ma saït
giæîa dáy âai vaì baïnh âai. Âãø coï læûc ma saït, cáön phaíi taûo læûc càng ban âáöu F
0
trãn caïc nhaïnh
âai.
Âãø taûo læûc càng ban âáöu F
0
trãn hai nhaïnh âai, âäöng thåìi âãø âiãöu chènh læûc càng âai khi
dáy âai bë daîn sau mäüt quaï trçnh laìm viãûc, coï thãø duìng troüng læåüng âäüng cå (âäüng cå âæåüc âàût
trãn táúm làõc - hçnh 8.3), duìng cå cáúu vêt âãø âáøy âäüng cå dëch chuyãøn trãn raînh træåüt (hçnh 8.4),
hoàûc duìng thãm baïnh càng âai (hçnh 8.2).
Bäü truyãön âai coï thãø duìng âãø truyãön chuyãøn âäüng giæîa hai truûc song song quay cuìng chiãöu
(hçnh 8.1), giæîa hai truûc song song quay ngæåüc chiãöu (hçnh 8.5), giæîa hai truûc cheïo nhau (hçnh
8.6) hay càõt nhau.
G Táúm làõc
K
håïp quay
H
çnh 8.3
Vêt âáøy
H
çnh 8.4
N
haïnh dáùn
1
2
3
O
1
O
2
N
haïnh bë dáùn
11
n,T
22
n,T
H
çnh 8.1
B
aïnh càn
g
âai
(
1
)
H
çnh 8.2
Baìi giaíng Cå såí thiãút kãú maïy - Pháön I - Lã Cung - Bäü män Nguyãn lyï Chi tiãút maïy - Khoa Sæ phaûm kyî thuáût 82
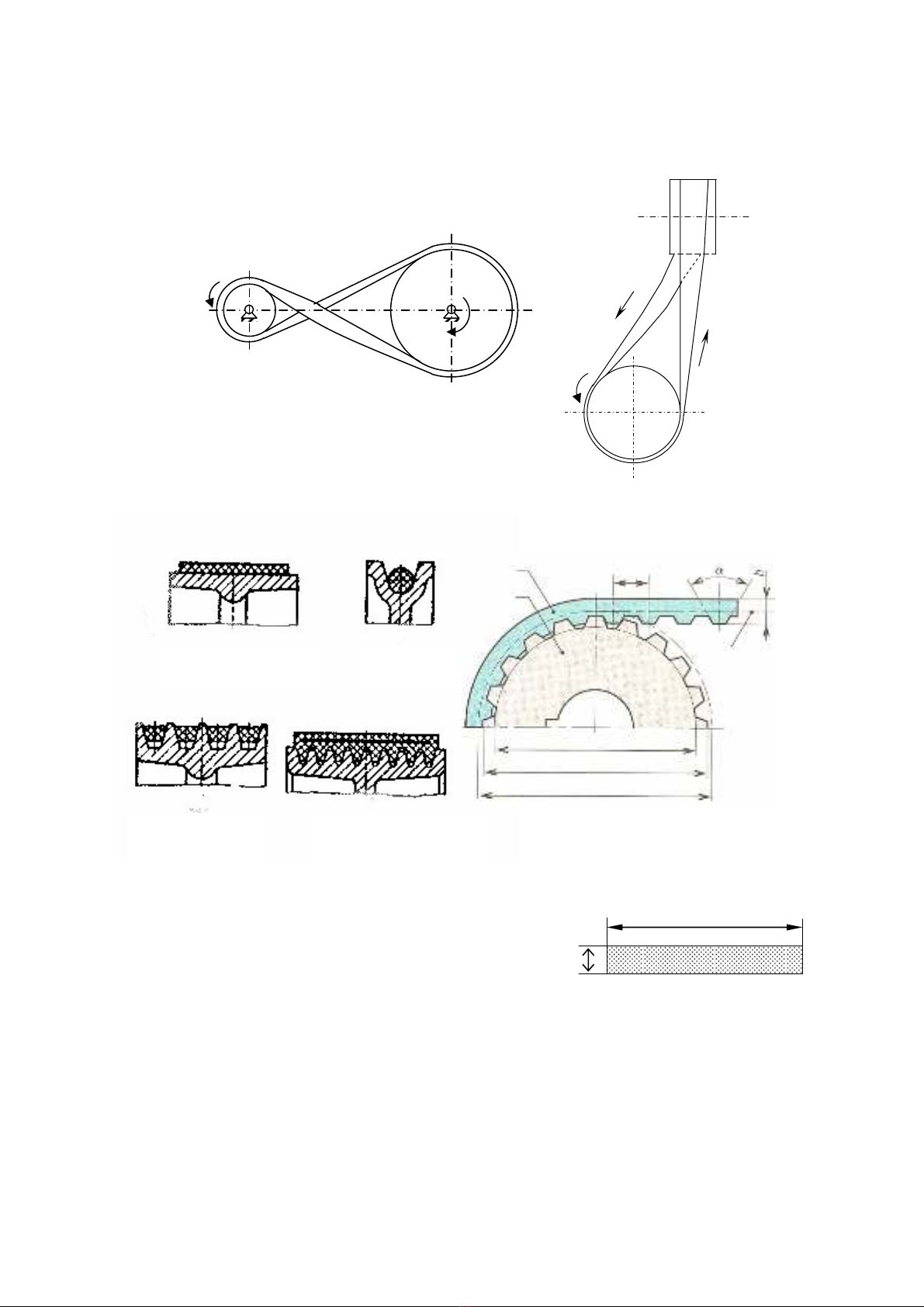
Dæûa trãn hçnh daûng tiãút diãûn âai, phán thaình: âai deût (hçnh 8.7a), âai thang (hçnh 8.7b), âai
troìn (hçnh 8.7c), âai hçnh læåüc (hay âai nhiãöu chãm - hçnh 8.7d). Ngoaìi ra, coìn duìng âai ràng,
truyãön læûc nhåì sæû àn khåïp cuía caïc ràng trãn âai vaì trãn baïnh âai (hçnh 8.8).
2. Caïc loaûi âai vaì kãút cáúu baïnh âai
a) Caïc loaûi âai
Âai deût
Gäöm âai da, âai vaíi cao su, âai såüi bäng, âai såüi
len, âai laìm bàòng caïc loaûi váût liãûu täøng håüp, trong âoï
âai vaíi cao su âæåüc sæí duûng räüng raîi hån caí.
¾
Âai vaíi cao su
Gäöm nhiãöu låïp vaíi bäng vaì cao su âæåüc sun-phua hoïa. Vaíi coï mäâun âaìn häöi låïn hån cao
su, âæåüc duìng âãø chëu pháön låïn taíi troüng, coìn cao su baío âaím cho âai laìm viãûc nhæ mäüt khäúi
nguyãn, baío vãû låïp vaíi khäng bë hæ haûi vaì náng cao hãû säú ma saït. Âai vaíi cao su coï âäü bãön
cao, âaìn häöi täút, êt chëu aính hæåíng cuía âäü áøm vaì thay âäøi nhiãût âäü, tuy nhiãn cao su khäng
chëu âæåüc dáöu, xàng vaì cháút kiãöm.
¾
Âai da
b
h
H
çnh 8.9
a) Âai deû
t
c) Âai t
r
oìn
b) Âai thang d) Âai hçnh læåüc
H
çnh 8.
7
H
çnh 8.8: Âai ràng
Z
C
Z
P
B
æåïc p
Chiãöu daìi
âæåìng
chia :
L
P
= p. Z
C
Â
æåìng kênh voìng chán
Â
æåìng kênh voìng âènh
Â
æåìng kênh voìng chia
O
1
O
2
Hçnh 8.5 : Hai truûc quay song song
vaì ngæåüc chiãöu nhau
Hçnh 8.6 : Hai truûc
quay cheïo nhau

Baìi giaíng Cå såí thiãút kãú maïy - Pháön I - Lã Cung - Bäü män Nguyãn lyï Chi tiãút maïy - Khoa Sæ phaûm kyî thuáût 83
Khaí nàng taíi täút, tuäøi thoü cao, chëu va âáûp täút, nhæng âàõt tiãön nãn êt duìng.
¾
Âai såüi bäng
Mãöm, reí, thêch håüp våïi váûn täúc cao. Do mãöm nãn coï thãø laìm viãûc våïi baïnh âai coï âæåìng kênh nhoí.
Khaí nàng taíi tháúp. Khäng duìng âæåüc åí nåi áøm æåït vaì nhiãût âäü cao.
¾
Âai såüi len
Dãût tæì såüi doüc bàòng len vaì såüi ngang bàòng bäng, chëu taíi troüng va âáûp täút, coï thãø laìm viãûc våïi baïnh
âai âæåìng kênh nhoí, nhæng âàõt tiãön nãn êt duìng.
¾
Âai laìm bàòng caïc váût liãûu täøng håüp
Âäü bãön, tuäøi thoü cao, chëu âæåüc va âáûp, coï thãø truyãön âæåüc cäng suáút låïn (âãún 150KW), coï thãø laìm
viãûc våïi váûn täúc cao (v ≤ 60m/s), baïnh âai coï âæåìng kênh nhoí.
Âai deût thæåìng chãú taûo thaình nhæîng bàng daìi, khi duìng tuìy theo khoaíng caïch truûc, âæåüc
càõt ra vaì näúi laûi thaình voìng kên bàòng caïch daïn, kháu hoàûc duìng caïc chi tiãút kim loaûi.
Chiãöu räüng b vaì chiãöu cao h cuía âai deût âæåüc tiãu chuáøn hoïa (hçnh 8.9).
Âai thang
Màût laìm viãûc cuía âai thang laì hai màût bãn, tiãúp
xuïc våïi caïc raînh hçnh thang tæång æïng trãn baïnh âai
(hçnh 8.7b).
Ma saït trãn âai thang coï thãø xem nhæ ma saït trãn
raînh, do âoï ma saït giæîa âai thang vaì baïnh âai låïn
hån trong âai deût, âäü baïm cuía âai thang täút hån trãn
âai deût. Goïc chãm cuía âai thang : ϕ = 40
0
.
Vãö cáúu taûo, âai thang coï hai loaûi: âai såüi xãúp (hçnh 8.11a) vaì âai såüi bãûn (hçnh 8.11b). Caïc
låïp såüi xãúp hoàûc såüi bãûn (1) âæåüc bäú trê åí låïp trung hoìa hoàûc âäúi xæïng våïi låïp trung hoìa. Låïp
cao su (2) chëu keïo, låïp cao su (3) chëu neïn, baío âaím cho âai laìm viãûc nhæ mäüt khäúi nguyãn
H
çnh 8.10b : Bäü truyãön âai deût
H
çnh 8.10c : Bäü tru
y
ãön âai ràn
g
b
t
b
h
y
o
b
h
y
o
ϕ
(4)
(3)
(2)
(1)
b
)
Âai så
ü
i bã
û
n
a
)
Âai så
ü
i xãú
p
H
çnh 8.11
H
çnh 8.10a : Bäü truyãön âai thang
Ba dáy âai
Baìi giaíng Cå såí thiãút kãú maïy - Pháön I - Lã Cung - Bäü män Nguyãn lyï Chi tiãút maïy - Khoa Sæ phaûm kyî thuáût 84
vaì laìm tàng âäü deío cho âai. Låïp voí (4) bàòng vaíi cao su boüc quanh âai baío vãû vaì laìm giaím
moìn cho âai (hçnh 8.11).
Âai thang âæåüc chãú taûo thaình voìng liãön, khäng phaíi näúi âáöu, nãn laìm viãûc ãm hån so våïi
âai deût näúi âáöu.
Kêch thæåïc tiãút diãûn âai âuåüc tiãu chuáøn hoïa: b, h, b
t
, ϕ, y
0
, våïi b
t
laì chiãöu räüng tênh toaïn.
Âäúi våïi âai thang thæåìng TCVN quy âënh 6 loaûi kêch thæåïc tiãút diãûn âai Z, O, A, B, C, D
(kêch thæåïc tiãút diãûn tàng dáön), tæång æïng våïi tiãu chuáøn Liãn xä ΓOCT : O, A, Б, B, Γ, Д.
Chiãöu daìi âai cuîng âæåüc tiãu chuáøn hoïa.
Âai hçnh læåüc
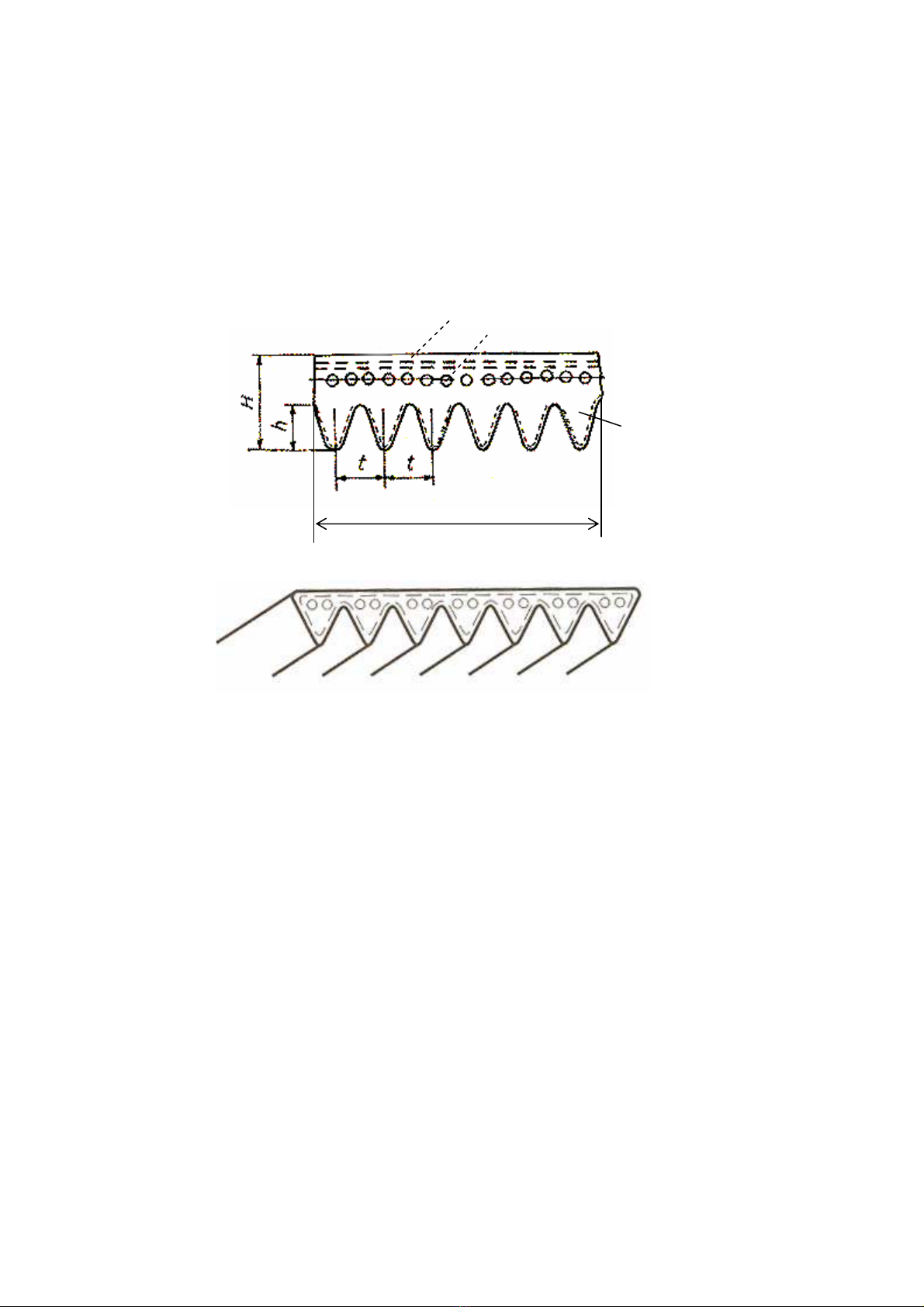
Gäöm nhiãöu gán phán bäú doüc theo chiãöu räüng vaì nàòm åí màût trong cuía âai (hçnh 8.12). Säú
gán thæåìng láúy chàôn : z = 2÷20 gán. Caïc gán naìy tiãúp xuïc våïi caïc raînh hçnh thang trãn baïnh
âai (hçnh 8.7d). Trong pháön phàóng cuía âai, coï mäüt säú låïp vaíi cao su vaì caïc såüi bãûn.
Âai hçnh læåüc phäúi håüp âæåüc æu âiãøm liãön khäúi vaì deío cuía âai deût våïi âäü baïm täút cuía âai
thang ⇒ khaí nàng taíi cao hån âai thang, vaì coï thãø màõc trãn baïnh âai coï âæåìng kênh nhoí hån,
laìm viãûc äøn âënh våïi tyí säú truyãön låïn hån.
Âai hçnh læåüc cuîng âæåüc chãú taûo thaình voìng liãön, khäng phaíi näúi âáöu.
Kêch thæåïc tiãút diãûn (b, H, t, h) vaì chiãöu daìi âai âæåüc tiãu chuáøn hoïa (hçnh 8.12). Tiãu
chuáøn Liãn xä ΓOCT quy âënh ba loaûi kêch thæåïc tiãút diãûn âai hçnh læåüc : K, Λ, M (kêch thæåïc
tiãút diãûn tàng dáön). Chiãöu daìi âai hçnh læåüc cuîng âæåüc tiãu chuáøn hoïa.
Âai ràng
Coï thãø xem âai ràng nhæ âai deût coï caïc ràng phán bäú âãöu åí màût trong cuía âai (hçnh 8.8,
hçnh 8.10c). Âai ràng âæåüc chãú taûo thaình voìng kên. Bäü truyãön âai ràng hoaût âäüng theo nguyãn
lyï àn khåïp, khäng coï træåüt, tyí säú truyãön låïn, hiãûu suáút cao, yãu cáöu læûc càng ban âáöu beï, do âoï
læûc taïc duûng lãn truûc vaì äø nhoí.
Thäng säú cå baín cuía âai ràng laì mäâun m = p/π, moâun âæåüc tiãu chuáøn hoïa.
b) Kãút cáúu baïnh âai
Kãút cáúu baïnh âai phuû thuäüc vaìo loaûi âai, khaí nàng cäng nghãû vaì quy mä saín xuáút.
låïp vaíi cao su
caïc såüi bãûn
b
H
çnh 8.12 : Âai hçnh læåüc
gán
Baìi giaíng Cå såí thiãút kãú maïy - Pháön I - Lã Cung - Bäü män Nguyãn lyï Chi tiãút maïy - Khoa Sæ phaûm kyî thuáût 85
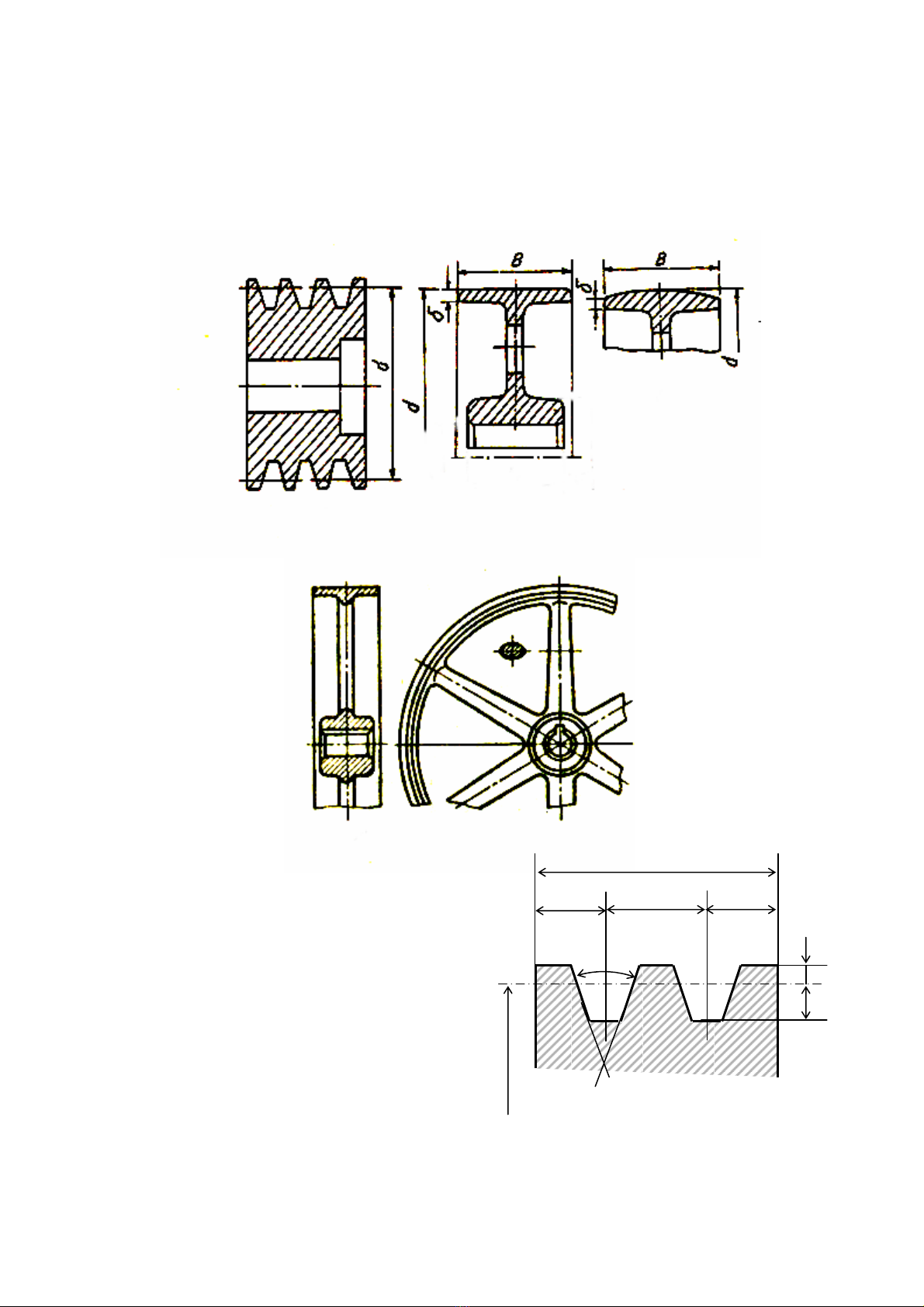
+ Baïnh âai coï âæåìng kênh d ≤ 100mm thæåìng âæåüc chãú taûo bàòng dáûp, âuïc, khäng khoeït
loîm (hçnh 8.13a).
+ Khi âæåìng kênh låïn hån duìng baïnh âai khoeït loîm, coï läù (hçnh 8.13b) hoàûc coï 4 âãún 6
nan hoa (hçnh 8.13d) âãø giaím båït khäúi læåüng ⇒ baïnh âai thæåìng gäöm coï ba pháön : vaình ngoaìi
tiãúp xuïc våïi âai, moayå âãø làõp lãn truûc vaì âéa hay nan hoa näúi vaình våïi moayå (hçnh 8.13d).
Kãút cáúu vaình baïnh âai phuû thuäüc vaìo
loaûi âai :
+ Våïi âai deût : Màût ngoaìi laì màût truû,
màût träúng (hçnh 8.13b, c) (màût träúng nhàòm
traïnh cho âai khoíi bë tuäüt khoíi baïnh âai
theo phæång doüc truûc).
+ Våïi âai thang: Kêch thæåïc raînh âai
hçnh thang âæåüc tiãu chuáøn hoïa (
,e,t,c,B
ϕ
)
(hçnh 8.14).
Våïi âai thang, goïc chãm ϕ trãn baïnh âai
âæåüc láúy nhoí hån goïc chãm trãn dáy âai: ϕ = 340, 360, 380, 400 båíi vç khi màõc âai lãn baïnh âai vaì bäü
truyãön laìm viãûc, pháön âai phêa trãn låïp trung hoìa chëu keïo, pháön dæåïi chëu neïn → goïc chãm thæûc tãú
cuía âai bë giaím xuäúng ⇒ cáön phaíi giaím goïc chãm cuía baïnh âai xuäúng cho phuì håüp, nhåì âoï taíi troüng
(b) Màût tr
u
û(c) Màût träúng (a)
Vaình ngoaìi
Nan hoa
Moayå
H
çnh 8.13
d
d
e e t
ϕ
B
c
a
H
çnh 8.14: Vaình baïnh âai thang











![Giáo trình Vật liệu cơ khí [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250909/oursky06/135x160/39741768921429.jpg)














