
Đ THI TH Đ I H C S 185Ề Ử Ạ Ọ Ố
I. PH N CHUNG ( Cho t t c thí sinh )Ầ ấ ả
Câu I ( 2 đi m ). ểCho hàm số
2 4
1
x
yx
−
=+
1) Kh o sát s bi n thiên và v đ th (C) c a hàm s .ả ự ế ẽ ồ ị ủ ố
2) Tìm trên đ th (C) hai đi m A, B đ i x ng nhau qua đ ng th ng MN, bi t ồ ị ể ố ứ ườ ẳ ế
( ) ( )
3;0 , 1; 1M N− − −
.
Câu II ( 2 đi m ).ể Gi i các ph ng trình, b t ph ng trình sau ả ươ ấ ươ
1)
( )
22
2
sin cos 2sin 2sin sin 3
1 cot 2 4 4
x x x x x
x
π π
+ − � �
� � � �
= − − −
� � � �
� �
+� � � �
� �
.
2)
( ) ( )
( )
2
2
4 1 2 10 1 3 2x x x+ < + − +
Câu III ( 1 đi m ). ểTính tích phân
( )
5
0
cos sinI x x x dx
π
= +
Câu IV ( 1 đi m ). ểCho hình h p ộABCD.A'B'C'D' có đáy là hình thoi c nh b ng a và góc ạ ằ
ᄋ
0
60BAD =
.
Hai m t chéo ặ( ACC'A' ) và ( BDD'B' ) cùng vuông góc v i m t ph ng đáy. G i M, N l n l t là trungớ ặ ẳ ọ ầ ượ
đi m c a CD, B'C', bi t r ng MN vuông góc v i BD'. Tính th tích c a kh i h p ABCD.A'B'C'D' .ể ủ ế ằ ớ ể ủ ố ộ
Câu V ( 1 đi m ). ểG i a, b, c là đ dài ba c nh c a m t tam giác có chu vi b ng 2. Ch ng minh r ngọ ộ ạ ủ ộ ằ ứ ằ
2 2 2
52 2 2
27 a b c abc + + + <
II. PH N ẦT CH NỰ Ọ ( Thí sinh ch đ c làm m t trong hai ph n A ho c B )ỉ ượ ộ ầ ặ
A. Theo ch ng trình Chu nươ ẩ
Câu VIa ( 2 đi m )ể
1) Trong m t ph ng t a đ Oxy cho tam giác ABC có đ nh ặ ẳ ọ ộ ỉ
( )
1;5B
và ph ng trình đ ng caoươ ườ
: 2 2 0AD x y+ − =
, đ ng phân giác góc C là ườ
' : 1 0CC x y− − =
. Tính t a đ các đ nh A và C.ọ ộ ỉ
2) Vi t ph ng trình đ ng th ng ế ươ ườ ằ
( )
∆
đi qua đi m ể
( )
1;1;1A
và vuông góc v i đ ng th ngớ ườ ẳ
( )
/
1 1
:1 1 2
x y z− −
∆ = =
và cách đi m ể
( )
2;0;1B
m t kho ng l n nh t.ộ ả ớ ấ
Câu VIIa ( 1 đi m )ể V i ớn là s nguyên d ng, ch ng minh h th cố ươ ứ ệ ứ
( ) ( ) ( )
( )
( ) ( )
2 2 2 2 2
1 2 3 1
2
2 3 ... 1 2
n n n
n n n n n n
n
C C C n C n C C
−
+ + + + − + =
B. Theo ch ng trình Nâng caoươ
Câu VIb ( 2 đi m )ể
1) Trong m t ph ng t a đ ặ ẳ ọ ộ Oxy cho đ ng tròn ườ
( )
2 2
3
:2
C x y+ =
và Parabol
( )
2
:P y x=
. Tìm trên (P)
các đi m ểM mà t đó k đ c hai ti p tuy n t i đ ng tr n ừ ẻ ượ ế ế ớ ườ ỏ (C) và hai ti p tuy n này t o v i nhauế ế ạ ớ
m t góc b ng ộ ằ 600.
2) Trong không gian t a đ Oxyz cho m t ph ng ọ ộ ặ ẳ
( )
: 2 1 0P x y z+ + − =
và đ ng th ng ườ ẳ (d) là giao
tuy n c a hai m t ph ng ế ủ ặ ẳ
( ) ( )
: 2 2 0 à : 2 2 0Q x y v R y z− − = + + =
. Vi t ph ng trình đ ng th ngế ươ ườ ẳ
( )
∆
đi qua giao đi m ểA c a ủ(d) và (P);
( )
∆
n m trong ằ(P) và góc t o b i hai đ ng th ng ạ ở ườ ẳ
( )
∆
và (d)
b ng ằ450.
Câu VIIb ( 1 đi m ).ể Ng i ta s d ng 5 cu n sách Toán, 6 cu n sách V t lí, 7 cu n sách Hóa h cườ ử ụ ố ố ậ ố ọ
( các cu n sách cùng lo i gi ng nhau ) đ làm gi i th ng cho 9 h c sinh, m i h c sinh đ c hai cu nố ạ ố ể ả ưở ọ ỗ ọ ượ ố
1
sách khác lo i. Trong s 9 h c sinh trên có hai b n Ng c và Th o. Tìm xác su t đ hai b n Ng c vàạ ố ọ ạ ọ ả ấ ể ạ ọ
Th o có gi i th ng gi ng nhau.ả ả ưở ố
H NG D N ƯỚ Ẫ
Câu I(2 đi m)1ể. Kh o sát s bi n thiên và v đ th hàm s ả ự ế ẽ ồ ị ố
2 4
1
x
yx
−
=+
* T p xác đinh ậ
{ }
\ 1D= −ᄋ
Gi i h n, ti m c n:ớ ạ ệ ậ
1 1
lim ; lim
x x
y y
− +
− −
= + = −
. Suy ra ph ng trình đ ng ti m c n đ ng ươ ườ ệ ậ ứ x = – 1
lim 2; lim 2
x x
y y
− +
= =
. Suy ra ph ng trình đ ng ti m c n ngang ươ ườ ệ ậ y = 2+
* S bi n thiên: ự ế
( ) ( ) ( )
2
6
' 0; ; 1 1;
1
y x
x
= > ∀ − − − +� � � �
+
nên hàm
s đ ng bi n trong t ng kho ng xác đ nh c a nó.ố ồ ế ừ ả ị ủ
* B ng bi n thiên ả ế
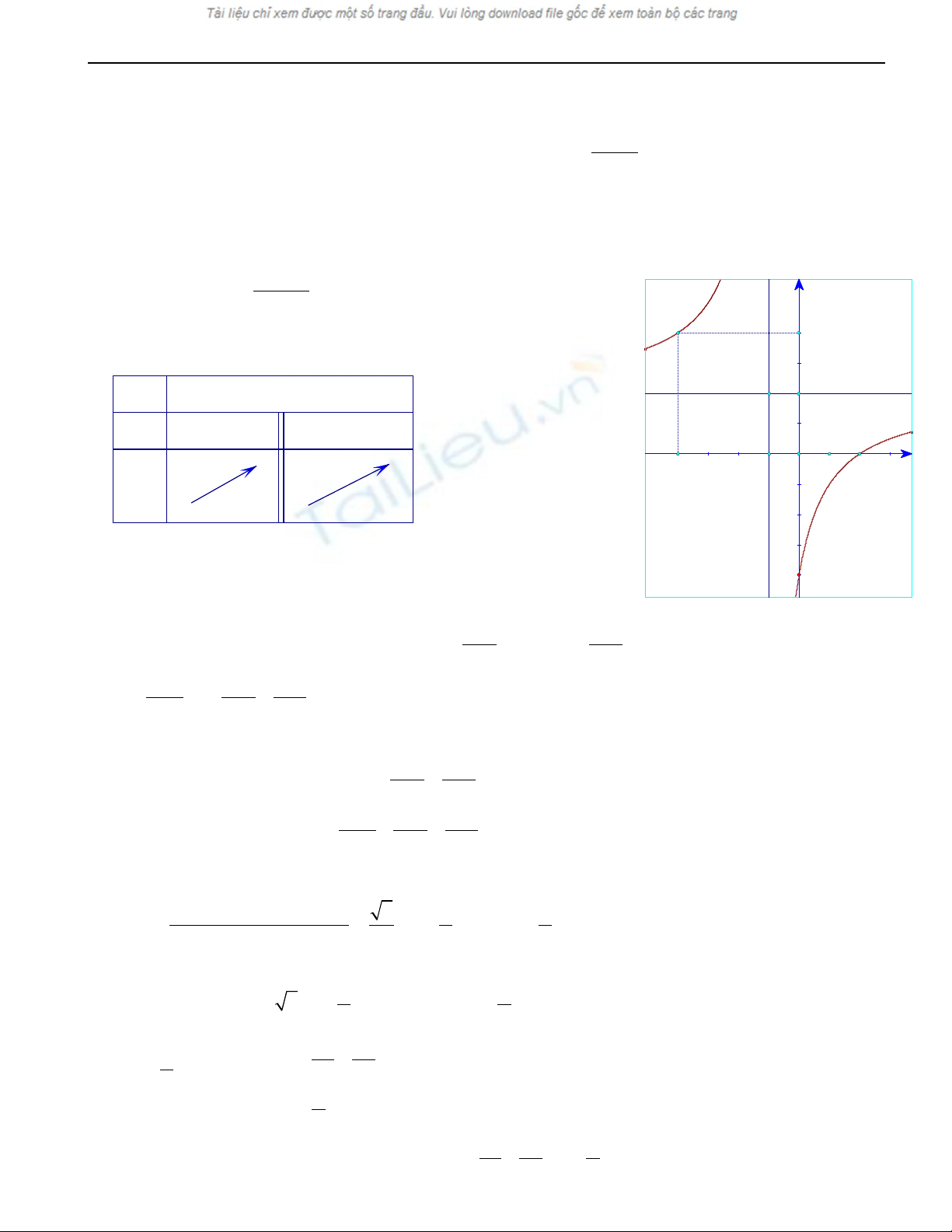
* Đ th : ồ ị
Đ th ph i đi qua cácồ ị ả
đi m đ c bi tể ặ ệ
( ) ( ) ( )
2,0 ; 0, 4 ; 4,4− −
Nh n xét: đ th có tâmậ ồ ị
đ i x ng là đi mố ứ ể
( )
1;2I−
Câu 1: 2) Tìm trên đ th hai đi m đ i x ng nhau ồ ị ể ố ứ
qua đ ng th ng MN, bi t ườ ẳ ế
( ) ( )
3;0 , 1; 1M N− − −
.
Ph ng trình đ ng th ng ươ ườ ẳ
( )
: 2 3 0MN x y+ + =
.
Xét hai đi m A, B trên đ th (C), ta có ể ồ ị
6 6
; 2 , ; 2 , , 1
1 1
A a B b a b
a b
� � � �
− − −
� � � �
+ +
� � � �
G i ọ
3 3
; 2
2 1 1
a b
Ia b
+
� �
− −
� �
+ +
� �
là trung đi m c a đo n đo n ABể ủ ạ ạ
Theo yêu c u c a bài toán ta cóầ ủ
( ) ( )
2
3 3 00
. 0 1 1 ...
6 6 0
7
2 1 1 2
a
b a
AB MN b
AB MN a b
I MN b a a
I MN
a b b
=�
− − + =
⊥=
=
� � � �
+ +
� � � �
� � �
+=
− − = −
+ +
=
uuur uuuur
V y ậ
( ) ( )
2;0 ; 0; 4A B −
ho c ặ
( ) ( )
2;0 ; 0; 4B A −
Câu 2: 1)
( )
22
2
sin cos 2sin 2sin sin 3
1 cot 2 4 4
x x x x x
x
π π
+ − � �
� � � �
= − − −
� � � �
� �
+� � � �
� �
.Đi u ki n xác đ nh ề ệ ị
sin 0x
hay
;x k k
π
Z
.Ph ng trình đã cho t ng đ ng v iươ ươ ươ ớ
( ) ( )
( )
2
cos 2 sin 2 sin 2 cos 2 sin cos 2 sin 1 0
4 4
3
cos 2 0 8 2 ,
4
2
sin 1 0 2
x x x x x x x
k
x
xk m Z
x m
x
π π
π π
π
ππ
� � � �
+ = − − − =�
� � � �
� � � �
� � = +
− =
� �
� � �
� �
= +
− =
So v i đi u ki n nghi m c a ph ng trình là ớ ề ệ ệ ủ ươ
( )
3; 2 ; ,
8 2 2
k
x x m k m Z
π π π π
= + = +
2
+
∞
-
∞
2
2
+
+
- 1
+
∞
-
∞
y'
y
x
x
y
- 4
4
I
2
- 1
- 4
2
O
1
Câu 2: 2)
( ) ( )
( )
2
2
4 1 2 10 1 3 2x x x+ < + − +
Đi u ki n xác đ nh ề ệ ị
3
2
x −
( ) ( )
( )
( ) ( )
( ) ( )
( )
( ) ( ) ( )
( )
( )
( ) ( )
2 2
2
2 2
2
2
2
2
22
2 10 1 3 2 1 3 2
4 1 2 10 1 3 2 4 1
1 3 2
11
2 10 4 1 2 10
4 1 11 3 2 2 10
1 3 2 1 3 2
x x x
x x x x
x
xx
x x x
xx x
xx
+ − + + +
+ < + − + + <�+ +
−
−
+ + � �
+
+ <� � �
� �
<+ + < +
+ + ��
+ +
1 1 1
3
2 4 2 3 2 2 10 3 2 3
x x x
x
x x x x
− −
� � −
� �
� � �
� � � <
+ + + < + + <
� �
� �
K t h p v i đi u ki n ta có t p nghi m c a b t ph ng trình là ế ợ ớ ề ệ ậ ệ ủ ấ ươ
{ }
3; 3 \ 1
2
S� �
= − −
� �
Câu III(1 đi m)ểTính tích phân
( )
5
0
cos sinI x x x dx
π
= +
*
( )
1 2
5 5
0 0 0
cos sin .cos . .sin .
I I
I x x x dx x x dx x x dx
π π π
= + = +
� � �
1 42 43 1 4 2 4 3
.
*
10 0 0
0 0
.cos . .sin sin . .sin cos 2I x x dx x x x dx x x x
π π
π π π
= = − = + = −
� �
* V i ớ
2
I
ta đ t ặ
( )
( )
2
2
2
0
8
1 cos cos
2 15
x t I x d x
π
π π
π
= − = − − =�
. * V y ậ
82
15
I
π
= −
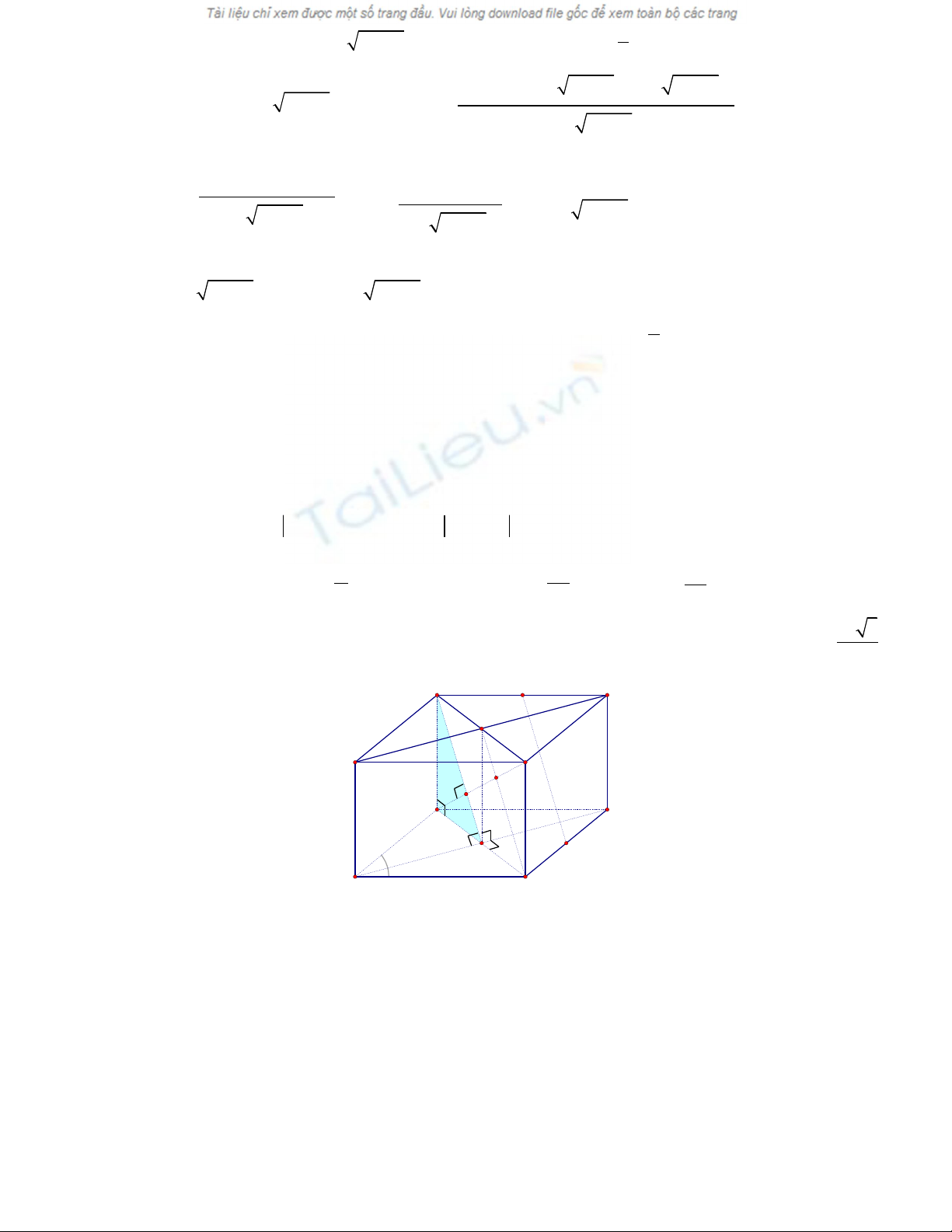
Câu IV(1 đi m) .ểTính theo a th tích hình chóp S.ABMNể * T gi thi t ta có ừ ả ế
2
2 0
3
sin 60 2
ABCD
a
S a= =
60
0
H
N
M
C'
O'
D'
A'
C
O
B
A
D
B'
* G i O, O' l n l t là tâm hai đáy ABCD và A'B'C'D' t gi thi t ọ ầ ượ ừ ả ế
( ) ( )
( ) ( )
( ) ( ) ( )
' '
' ' '
' ' ' ' '
ACC A ABCD
BDD B ABCD OO ABCD
OO ACC A BDD B
⊥⊥ ⊥�
=
I
mà OO' // AA' , nên ta có hình h p đã cho là hìnhộ
h p đ ngộ ứ
3












![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)




![Đề thi học kì 2 Vật lý lớp 11: Đề minh họa [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250709/linhnhil/135x160/711752026408.jpg)








