
Tuy n sinh khu v c Tp Đông Hà và các huy n lân c n các l p 9, 10, 11, 12, các môn Toán, Lý, Hoá,…Các em có thể ự ệ ậ ớ ể
h c t i nhàọ ạ theo nhóm ho c cá nhân, ho c h c t i trung tâm 40 h c sinh/ 1l p. Cung c p tài li u, đ thi tr cặ ặ ọ ạ ọ ớ ấ ệ ề ắ
nghi m mi n phí . ệ ế
S GIÁO D C ĐÀO T O Ở Ụ Ạ KỲ THI VÀO L P 10 CHUYÊN LAMỚ
S NƠ
THANH HOÁ NĂM H C 2012 - 2013Ọ
Môn thi : TOÁN
(Đ g m có 01 trang)ề ồ (Môn chung cho t t c c thí sinh)ấ ả
Th i gian làm bài :120 phút (Không k th i gian giao đ )ờ ể ờ ề
Ngày thi : 17 tháng 6 năm 2012
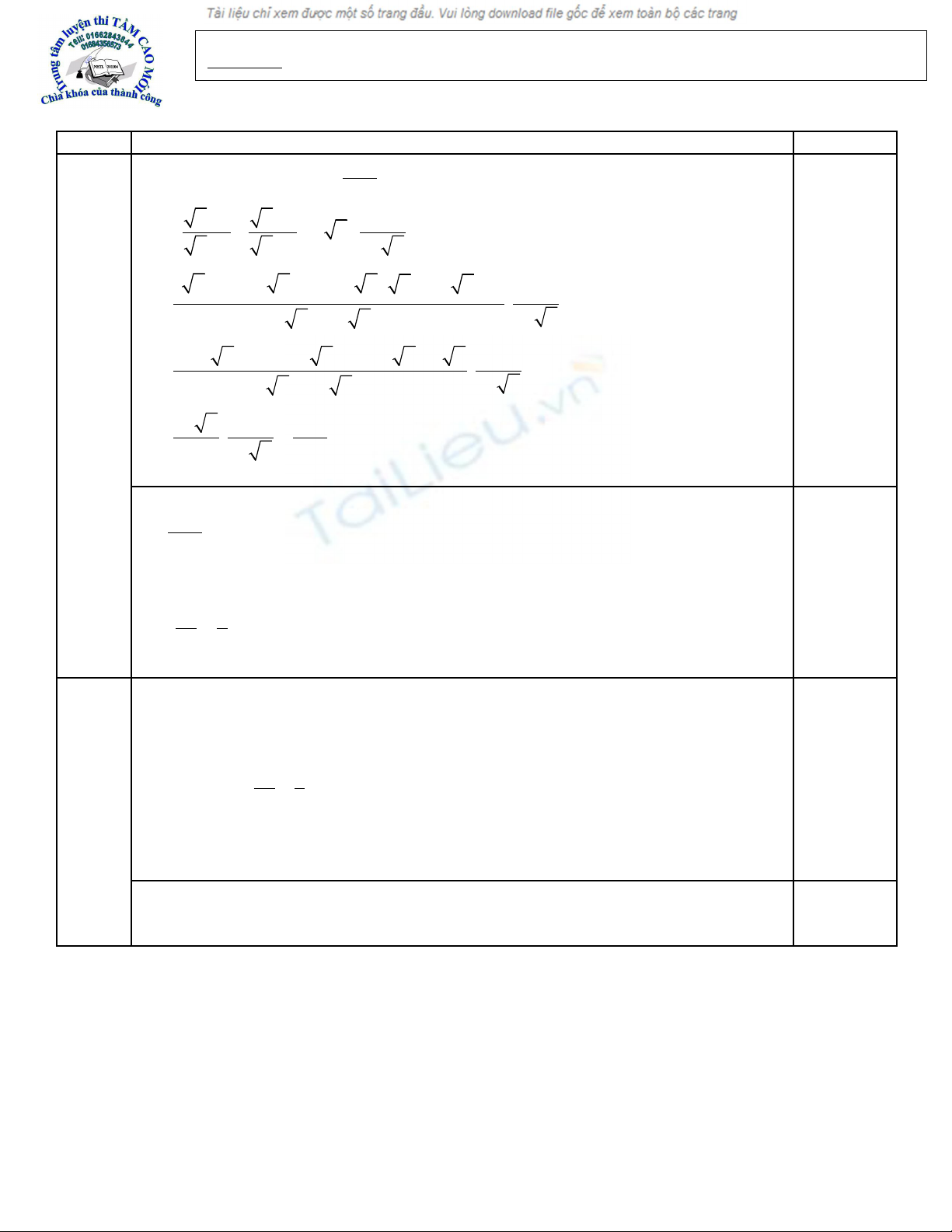
Câu 1: (2.0 đi m ) Cho bi u th c :ể ể ứ
1 1 1
4
1 1 2
a a
P a
a a a a
� �
+ −
= − +
� �
� �
− +
� �
, (V i a > 0 , a ớ≠1)
1. Ch ng minh r ng : ứ ằ
2
1
Pa
=−
2. Tìm giá tr c a a đ P = aị ủ ể
Câu 2 (2,0 đi m ) : Trong m t ph ng to đ Oxy, cho Parabol (P) : y = xể ặ ẳ ạ ộ 2 và đưng th ng (d) : y = 2x + 3ờ ẳ
1. Ch ng minh r ng (d) và (P) có hai đi m chung phân bi t ứ ằ ể ệ
2. G i A và B là các đi m chung c a (d) và (P) . Tính di n tích tam giác OAB ( O là g c to đ )ọ ể ủ ệ ố ạ ộ
Câu 3 (2.0 đi m) : Cho phểng trình : xươ 2 + 2mx + m2 – 2m + 4 = 0
1. Gi i phảng trình khi m = 4ơ
2. Tìm m đ phể ư ng trình có hai nghi m phân bi tơ ệ ệ
Câu 4 (3.0 đi m) : Cho đểng tròn (O) có đườ ng kính AB c đ nh, M là m t đi m thu c (O) ( M khác A vàờ ố ị ộ ể ộ
B ) . Các ti p tuy n c a (O) t i A và M c t nhau C. Đế ế ủ ạ ắ ở ư ng tròn (I) đi qua M và ti p xúc v i đờ ế ớ ư ng th ngờ ẳ
AC t i C. CD là đạng kính c a (I). Ch ng minh r ng:ờ ủ ứ ằ
1. Ba đi m O, M, D th ng hàngể ẳ
2. Tam giác COD là tam giác cân
3. Đ ng th ng đi qua D và vuông góc v i BC luôn đi qua m t đi m c đ nh khi M di đ ng trên đờ ẳ ớ ộ ể ố ị ộ ư ngờ
tròn (O)
Câu 5 (1.0 đi m) : Cho a,b,c là các s dể ố ng không âm tho mãn : ươ ả
2 2 2 3abc+ + =
Ch ng minh r ng : ứ ằ
2 2 2
1
2 3 2 3 2 3 2
a b c
a b b c c a
+ +
+ + + + + +
Tr n H i Nam - Tell: 01662 843844 – TT luy n thi T m Cao M i Tell: 01684 356573 – 0533564384 – 0536513844 – 0944323844ầ ả ệ ầ ớ 1
Đ CHÍNH TH CỀ Ứ
Tuy n sinh khu v c Tp Đông Hà và các huy n lân c n các l p 9, 10, 11, 12, các môn Toán, Lý, Hoá,…Các em có thể ự ệ ậ ớ ể
h c t i nhàọ ạ theo nhóm ho c cá nhân, ho c h c t i trung tâm 40 h c sinh/ 1l p. Cung c p tài li u, đ thi tr cặ ặ ọ ạ ọ ớ ấ ệ ề ắ
nghi m mi n phí . ệ ế
BÀI GI IẢ
CÂU N I DUNGỘĐI MỂ
1
1. Ch ng minh r ng : ứ ằ
2
1
Pa
=−
1 1 1
4
1 1 2
a a
P a
a a a a
� �
+ −
= − +
� �
� �
− +
� �
( ) ( ) ( ) ( )
( ) ( )
2 2
1 1 4 1 1 1
.2
1 1
a a a a a
Pa a
a a
+ − − + + −
=+ −
( ) ( )
2 1 2 1 4 4 1
.2
1 1
a a a a a a a
Pa a
a a
+ + − + − + −
=+ −
4 1 2
.
1 1
2
a a
Pa a
a a
= =
− −
(ĐPCM)
1.0
2. Tìm giá tr c a a đ P = a. P = a ị ủ ể
=>
2
22 0
1a a a
a= => − − =
−
.
Ta có 1 + 1 + (-2) = 0, nên phưng trình có 2 nghi mơ ệ
a1 = -1 < 0 (không tho mãn đi u ki n) - Lo iả ề ệ ạ
a2 =
22
1
c
a
−= =
(Tho mãn đi u ki n)ả ề ệ
V y a = 2 thì P = aậ
1.0
21. Ch ng minh r ng (d) và (P) có hai đi m chung phân bi tứ ằ ể ệ
Hoành đ giao đi m độ ể ng th ng (d) và Parabol (P) là nghi m c a phườ ẳ ệ ủ ư ng trìnhơ
x2 = 2x + 3 => x2 – 2x – 3 = 0 có a – b + c = 0
Nên ph ng trình có hai nghi m phân bi tươ ệ ệ
x1 = -1 và x2 =
33
1
c
a
−= =
V i xớ1 = -1 => y1 = (-1)2 = 1 => A (-1; 1)
V i xớ2 = 3 => y2 = 32 = 9 => B (3; 9)
V y (d) và (P) có hai đi m chung phân bi t A và Bậ ể ệ
1.0
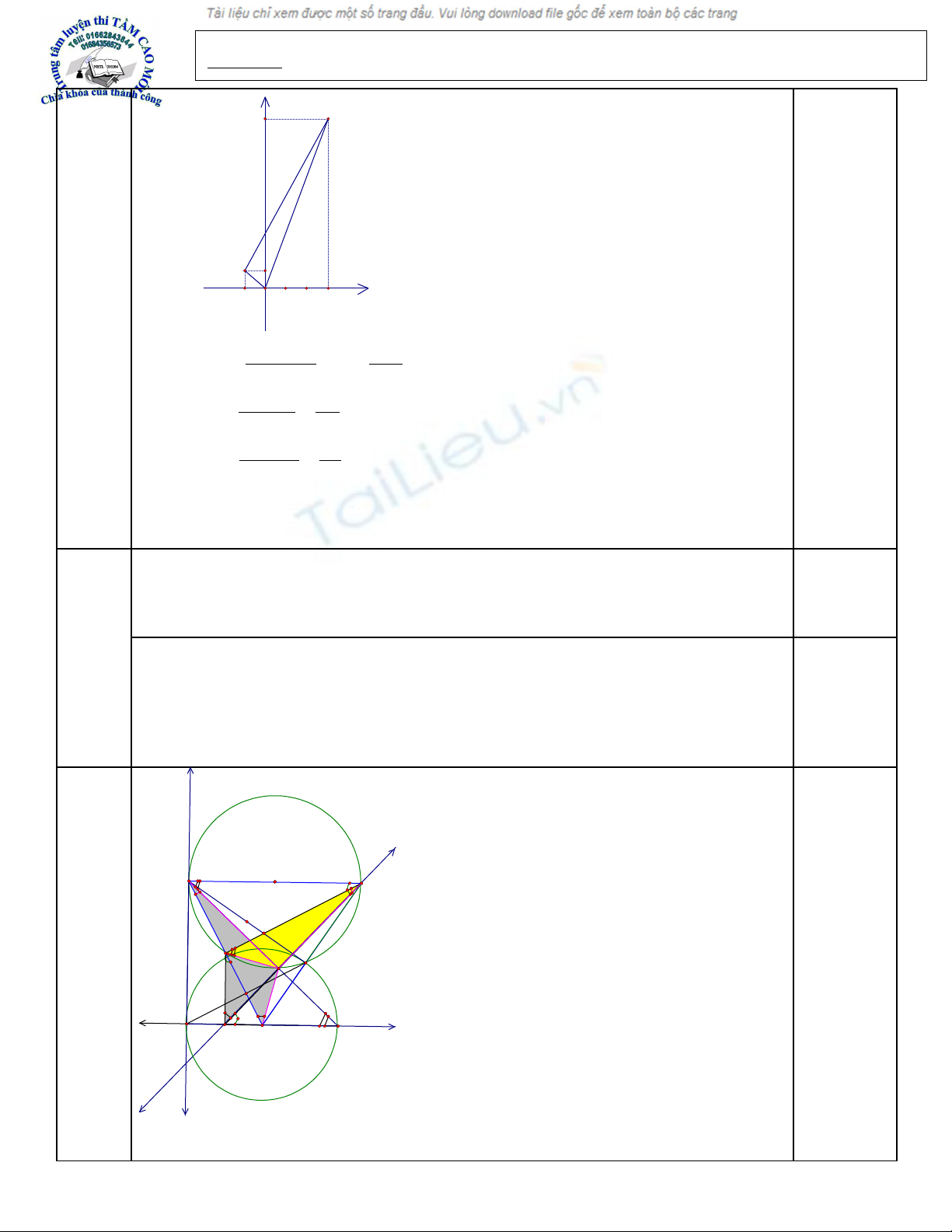
2. G i A và B là các đi m chung c a (d) và (P) . Tính di n tích tam giác OAB ( O làọ ể ủ ệ
g c to đ )ố ạ ộ
Ta bi u di n các đi m A và B trên m t ph ng to đ Oxy nhể ễ ể ặ ẳ ạ ộ ư hình vẽ
1.0
Tr n H i Nam - Tell: 01662 843844 – TT luy n thi T m Cao M i Tell: 01684 356573 – 0533564384 – 0536513844 – 0944323844ầ ả ệ ầ ớ 2
Tuy n sinh khu v c Tp Đông Hà và các huy n lân c n các l p 9, 10, 11, 12, các môn Toán, Lý, Hoá,…Các em có thể ự ệ ậ ớ ể
h c t i nhàọ ạ theo nhóm ho c cá nhân, ho c h c t i trung tâm 40 h c sinh/ 1l p. Cung c p tài li u, đ thi tr cặ ặ ọ ạ ọ ớ ấ ệ ề ắ
nghi m mi n phí . ệ ế
1
D
C
B
A
9
3
-1
0
1 9
. .4 20
2 2
ABCD
AD BC
S DC
+ +
= = =
. 9.3 13,5
2 2
BOC
BC CO
S= = =
. 1.1 0,5
2 2
AOD
AD DO
S= = =
Theo công th c c ng di n tích ta có:ứ ộ ệ
S(ABC) = S(ABCD) - S(BCO) - S(ADO)
= 20 – 13,5 – 0,5 = 6 (đvdt)
3
1. Khi m = 4, ta có ph ng trình ươ
x2 + 8x + 12 = 0 có ∆’ = 16 – 12 = 4 > 0
V y phậ ư ng trình có hai nghi m phân bi tơ ệ ệ
x1 = - 4 + 2 = - 2 và x2 = - 4 - 2 = - 6
1.0
2. Tìm m đ phểng trình có hai nghi m phân bi tươ ệ ệ
x2 + 2mx + m2 – 2m + 4 = 0
Có D’ = m2 – (m2 – 2m + 4) = 2m – 4
Đ phểng trình có hai nghi m phân bi t thì D’ > 0ươ ệ ệ
=> 2m – 4 > 0 => 2(m – 2) > 0 => m – 2 > 0 => m > 2
V y v i m > 2 thì phậ ớ ng trình có hai nghi m phân bi tươ ệ ệ
1.0
4
1
2
N
K
H
D
I
C
O
A
B
M
1. Ba đi m O, M, D th ng hàng:ể ẳ
Ta có MC là ti p tuy n c a đ ng tròn (O) ế ế ủ ườ ⇒ MC ⊥ MO (1)
1.0
Tr n H i Nam - Tell: 01662 843844 – TT luy n thi T m Cao M i Tell: 01684 356573 – 0533564384 – 0536513844 – 0944323844ầ ả ệ ầ ớ 3













![Dàn ý và bài văn mẫu nghị luận xã hội ôn thi vào lớp 10: Tài liệu [mô tả/định tính]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250824/levanphuong15081979@gmail.com/135x160/23851756089220.jpg)












