SỞ GD & ĐT VĨNH PHÚC
TRƯỜNG THPT TRẦN PHÚ
ĐỀ KHẢO SÁT ĐỘI TUYỂN TOÁN LẦN 2
Năm học: 2021 - 2022
Môn: Toán – Lớp 10
Thời gian làm bài: 180 phút, không kể thời gian phát đề
Câu 1: (1 điểm) Cho Parabol
2
:22Pyx x
và đường thẳng
:21dy x . Biết
P và
d cắt nhau tại
hai điểm phân biệt A và B . Tính độ dài đoạn
B
Câu 2: (1 điểm) Tìm tập xác định của hàm số 2
1
41912
yxx
.
Câu 3: (1 điểm) Tìm tất cả các giá trị của tham số m để hệ bất phương trình
2540
0
xx
xm
có nghiệm.
Câu 4: (2 điểm)
a) Giải phương trình 2
3 + 2 = 3 2xx xx
b) Giải hệ phương trình:
(
23 2
42
1
211
xxyxyxyy
xyxyx
ì
ï+-+-=
ï
í
ï+- -=
ï
î
Câu 5: (1 điểm) Gọi 12
;
x là hai nghiệm của phương trình 01
2 mmxx .
Đặt )1(2
64
21
2
2
2
1
21
xxxx
xx
A
. Tìm giá trị của tham số mđể
đạt giá trị nhỏ nhất.
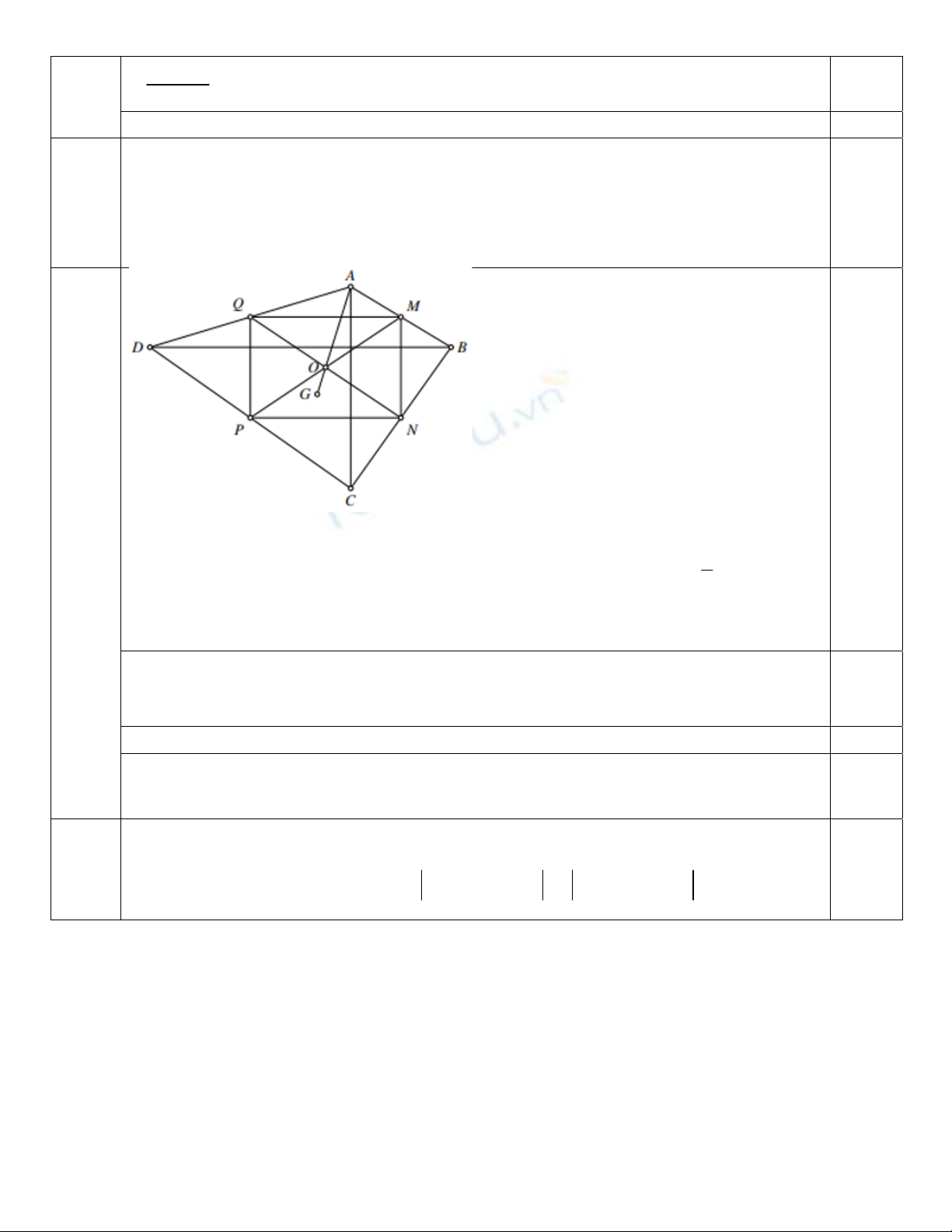
Câu 6: (1 điểm) Cho tứ giác ABCD . Gọi
, N, P, Q lần lượt là trung điểm của
B, BC , CD ,DA . Gọi
O là giao điểm của
P và NQ , G là trọng tâm của tam giác BCD . Chứng minh rằng ba điểm
,
O, G thẳng hàng.
Câu 7: (1 điểm) Cho tam giác ABC là tam giác đều cạnh bằng a,
là điểm di động trên đường thẳng AC .
Tìm giá trị nhỏ nhất của biểu thức 3TMAMBMC MAMBMC
.
Câu 8: (1 điểm) Cho tứ giác lồi ABCD có AC BD và nội tiếp đường tròn tâm O bán kính 1010R. Đặt
diện tích tứ giác ABCD bằng S và ,,,
BaBCbCDcDAd. Tính giá trị biểu thức
4
ab cd ad bc
TS
.
Câu 9: (1 điểm) Cho ,
là các số thực thay đổi. Tìm giá trị nhỏ nhất của biểu thức
2
22
112Ax y x yy
------------HẾT------------
Họ và tên thí sinh..................................................................................................SBD..........................................