Đề kiểm tra 1 tiết Giải tích 12 chương 3 năm 2017-2018 có đáp án - Trường THPT Trần Nhật Duật

TRƯỜNG THPT<br /> TRẦN NHẬT DUẬT<br /> <br /> ĐỀ KIỀM TRA 1 TIẾT<br /> CHƯỚNG III - GIẢI TÍCH 12<br /> Thời gian làm bài: 45 phút;<br /> Mã đề thi 002<br /> <br /> Câu 1. Khẳng định nào sau đây Sai<br /> A.<br /> <br /> x 1<br /> C<br />  1<br /> <br /> <br />  x dx <br /> <br /> (  1)<br /> <br /> B.<br /> <br /> <br /> <br /> dx<br />  ln x  C .<br /> x<br /> <br /> D.  e x dx  e x  C.<br /> <br /> C.  sin xdx  cosx  C.<br /> <br /> 2<br /> <br /> Câu 2. F (x ) là một nguyên hàm của hàm số y = xe x . Khẳng định nào sau đây Sai<br /> A. F (x )=<br /> <br /> 1 x2<br /> e + 2.<br /> 2<br /> <br /> B. F (x )=<br /> <br /> 1 x2<br /> e +5 .<br /> 2<br /> <br /> (<br /> <br /> )<br /> <br /> C. F (x )= -<br /> <br /> Câu 3. Tìm nguyên hàm của hàm số f  x   2 x <br /> B.<br /> <br />  f  x  dx  x<br /> <br /> 1<br /> C  f  x  dx  x 2  ln | x |  e3 x  C.<br /> 3<br /> <br /> D.<br /> <br /> f  x  dx <br /> <br />  f  x  dx  x<br /> <br /> 2<br /> <br /> Câu 4. Tìm nguyên hàm của hàm số f  x  <br /> A.<br /> C.<br /> <br /> 1<br /> <br />  4 x<br /> <br /> 2<br /> <br /> dx <br /> <br /> 1<br /> <br />  4 x<br /> <br /> 2<br /> <br /> D. F (x )= -<br /> <br /> 2<br /> 1<br /> 2 - ex .<br /> 2<br /> <br /> (<br /> <br /> )<br /> <br /> 1 3x<br /> e .<br /> x<br /> <br />  ln | x |  e3 x  C.<br /> <br /> A.<br /> <br /> 1 x2<br /> e +C.<br /> 2<br /> <br /> <br /> <br /> 2<br /> <br /> 1<br />  ln x  e3 x  C.<br /> 3<br /> <br /> x2<br />  ln | x | e3 x  C .<br /> 2<br /> <br /> 1<br /> .<br /> 4  x2<br /> <br /> 1 2 x<br /> ln<br /> C<br /> 2 2 x<br /> <br /> 1<br /> <br />  4 x<br /> <br /> B.<br /> <br /> 1 2x<br /> dx  ln<br /> C<br /> 2 2 x<br /> <br /> D.<br /> <br /> 1<br /> <br />  4 x<br /> <br /> 2<br /> <br /> dx  ln<br /> <br /> dx  ln<br /> <br /> 2<br /> <br /> 2 x<br /> C<br /> 2 x<br /> <br /> 2 x<br /> C<br /> 2 x<br /> <br /> Câu 5.  (e x  1) 2 dx bằng:<br /> 1 2x<br /> e  2e x  x  C<br /> 2<br /> 1<br /> Câu 6. Nguyên hàm của hàm số f ( x) <br /> là<br /> 3x  1<br /> 1<br /> 1<br /> A. ln 3 x  1  C<br /> B. ln 3 x  1  C<br /> 2<br /> 3<br /> Câu 7. Tìm nguyên hàm của hàm số f ( x)  4.9 x .<br /> <br /> A. e 2 x  2e x  C<br /> <br /> A.<br /> <br /> <br /> <br /> f ( x) dx <br /> <br /> B.<br /> <br /> 4.9 x<br />  C .B.<br /> ln 9<br /> <br /> <br /> <br /> f ( x) dx <br /> <br /> b<br /> <br /> d<br /> <br /> Câu 8. Tính I   f ( x) dx biết rằng<br /> a<br /> <br /> A. I  3<br /> <br /> 4.9 x 1<br /> C .<br /> x 1<br /> <br /> B. I  1<br /> <br /> <br /> a<br /> <br /> C. e x  1  C<br /> <br /> C.<br /> <br /> C.<br /> <br /> D. e x  C<br /> <br /> 1<br /> ln  3 x  1  C<br /> 3<br /> <br />  f ( x)dx  4.9<br /> <br /> x<br /> <br /> D. ln 3 x  1  C<br /> <br /> ln 9  C . D.<br /> <br /> d<br /> <br /> C. I  1<br /> <br /> <br /> <br /> D. I  2<br /> <br /> B. F  3  <br /> <br /> 8<br /> <br /> <br /> <br /> x<br /> <br /> e2  17e<br /> .<br /> 9<br /> <br /> C<br /> <br /> b<br /> <br /> Câu 10. Biết F ( x) là một nguyên hàm của hàm số f ( x)  e 3<br /> A. F  3 <br /> <br /> x 1<br /> <br /> f ( x) dx  1; I   f ( x) dx  2; ( a  d  b) .<br /> <br /> 2x<br /> Câu 9. Tìm nguyên hàm của hàm số f ( x)  4sin .<br /> 3<br /> 8<br /> 2x<br /> 2x<br /> 2x<br /> A. f ( x)dx  cos  C. B. f ( x)dx  6cos  C. C. f ( x)dx  6cos  C. D.<br /> 3<br /> 3<br /> 3<br /> 3<br /> <br /> <br /> <br />  f ( x)dx  4 x.9<br /> <br /> e 2  5e<br /> .<br /> 3<br /> <br /> 1<br /> <br /> 2x<br /> <br />  f ( x)dx   3 cos 3  C.<br /> <br /> và F  0   2e . Tính F  3 .<br /> <br /> C. F  3  e 2  e .<br /> <br /> D. F  3  3e 2  e .<br /> <br /> 3<br /> <br /> Câu 11. Biết<br /> <br />  ln xdx  a ln 3  b ln 2  1; a, b <br /> <br /> . Khi đó, giá trị của a  b là:<br /> <br /> 2<br /> <br /> Trang 1/5 - Mã đề thi 001<br /> <br /> A. 5 B. 5 C. 1<br /> <br /> D. 6<br /> e2<br /> <br /> 3ln x  2<br /> dx  a  b ln 3 (với a, b  ). Giá trị của a 2  b 2 bằng<br /> x  ln x  1<br /> 1<br /> B. 25<br /> C. 52<br /> D. 61<br /> <br /> Câu 12: Cho tích phân I  <br /> A. 45<br /> <br /> 2<br /> <br /> Câu 13: Cho các tích phân<br /> <br /> 4<br /> <br /> 2<br /> <br /> f ( x)dx  3, f ( x)dx  5 .Tính I   f (2 x)dx.<br /> <br /> <br /> 0<br /> <br /> 2<br /> <br /> A. I  2 .<br /> <br /> 0<br /> <br /> B. I  3 .<br /> <br /> <br /> C. I  4<br /> <br /> D. I  8<br /> <br /> 1 <br />  . Giá trị của a.b là<br /> a b<br /> C. 24<br /> D. 2<br /> <br /> Câu 15:Tính tích phân sau:  4 (1  x) cos2 xdx <br /> 0<br /> <br /> B. 12<br /> <br /> A. 32<br /> <br /> 2<br /> <br /> Câu 16. Cho hàm số f ( x ) có đạo hàm trên đoạn 1; 2 , f (1) 1 và f (2)  2 . Tính I   f '( x)dx .<br /> 1<br /> <br /> I 1<br /> <br /> B. I   1<br /> e<br /> <br /> Câu 17: Biết rằng<br /> <br /> <br /> <br /> <br /> <br /> C. I  3<br /> <br /> <br /> <br /> 1  3 ln x ln x<br /> x<br /> <br /> 1<br /> <br /> 7<br /> D. I <br /> 2<br /> <br /> dx <br /> <br /> a<br /> a<br /> , trong đó a , b là hai số nguyên dương và<br /> là phân số tối giản.<br /> b<br /> b<br /> <br /> Tính giá trị biểu thức P  a  b .<br /> A. – 19 .<br /> B. – 18.<br /> C. – 2.<br /> D. – 21.<br /> Câu 18. Diện tích hình phẳng phần bôi đen trong hình sau được tính theo công thức:<br /> b<br /> <br /> c<br /> <br /> b<br /> <br /> A. S   f  x  dx   f  x  dx<br /> a<br /> <br /> b<br /> <br /> c<br /> <br /> b<br /> <br /> a<br /> <br /> b<br /> <br /> c<br /> <br /> C. S   f  x  dx   f  x  dx<br /> b<br /> <br /> c<br /> <br /> B. S   f  x  dx   f  x  dx<br /> D. S <br /> <br /> a<br /> <br />  f  x  dx<br /> a<br /> <br /> Câu 19. Diện tích hình phẳng giới hạn bởi đồ thị y  x(e  1) và<br /> <br /> y  (1  e x ) x :<br /> 1<br /> A. 2  e B. 2<br /> 2<br /> <br /> C.<br /> <br /> 1<br /> e 1<br /> 2<br /> <br /> D.<br /> <br /> 3<br /> 1<br /> e<br /> <br /> Câu 20: Cho hình thang giới hạn bởi y  3x; y  x; x  0; x  1. Tính thể tích vật thể tròn xoay khi nó xoay<br /> 8<br /> 8 2<br /> B.<br /> C. 8 2<br /> D. 8<br /> 3<br /> 3<br /> Câu 21 : Thể tích vật thể hình phẳng giới hạn bởi đồ thị y  x ln x và y  0; x  1; x  e quay xung quanh<br /> <br /> quanh Ox<br /> <br /> trục Ox là<br /> <br /> A.<br /> <br /> A.<br /> <br /> 2e3  1<br /> 2e3  1<br /> B.<br /> 9<br /> 9<br /> <br /> C.<br /> <br /> e3  2<br /> 9<br /> <br /> D.<br /> <br /> <br /> <br /> e3  2<br /> 9<br /> <br /> Câu 22: Một vật chuyển động với gia tốc a (t )  20 1  2t<br /> <br /> <br /> <br /> 2<br /> <br /> (m / s 2 ) . Khi t  0 thì vận tốc của vật là<br /> <br /> 30(m / s ) . Tính quãng đường vật đó di chuyển sau 2 giây ( m là mét, s là giây).<br /> A. 46 m .<br /> <br /> B. 48 m .<br /> <br /> C. 47 m .<br /> <br /> D. 49 m .<br /> <br /> 13<br /> t  8 và lúc<br /> 5<br /> đầu bồn không chứa nước. Tìm mức nước ở bồn sau khi bơm được 6 giây (làm tròn kết quả đến hàng phần<br /> trăm)<br /> A. 2,67<br /> B. 2,65<br /> C. 2,66<br /> D. 2,64<br /> Câu 24: Cho hình vẽ như dưới phần tô đậm là phần giới hạn bởi đồ thị<br /> y  x 2  2 x với trục Ox. Thể tích khối tròn xoay quay phần giới hạn quanh<br /> trục Ox bằng:<br /> 32<br /> 16<br /> 32<br /> 16<br /> <br /> <br /> <br /> A.<br /> B.  C.<br /> D.<br /> 5<br /> 5<br /> 15<br /> 15<br /> <br /> Câu 23. Gọi h  t  (cm) là mức nước ở bồn chứa sau khi bơm nước được t giây. Biết rằng h '  t  <br /> <br /> Trang 2/5 - Mã đề thi 001<br /> <br /> Câu 25:Vòm cửa lớn của một trung tâm văn hoá có dạng hình Parabol.<br /> Người ta dự định lắp cửa kính cường lực cho vòm cửa này. Hãy tính diện<br /> tích mặt kính cần lắp vào biết rằng vòm cửa cao 8m và rộng 8m (như hình vẽ<br /> 28 2<br /> 26<br /> 128 2<br /> 131 2<br /> A.<br /> B. 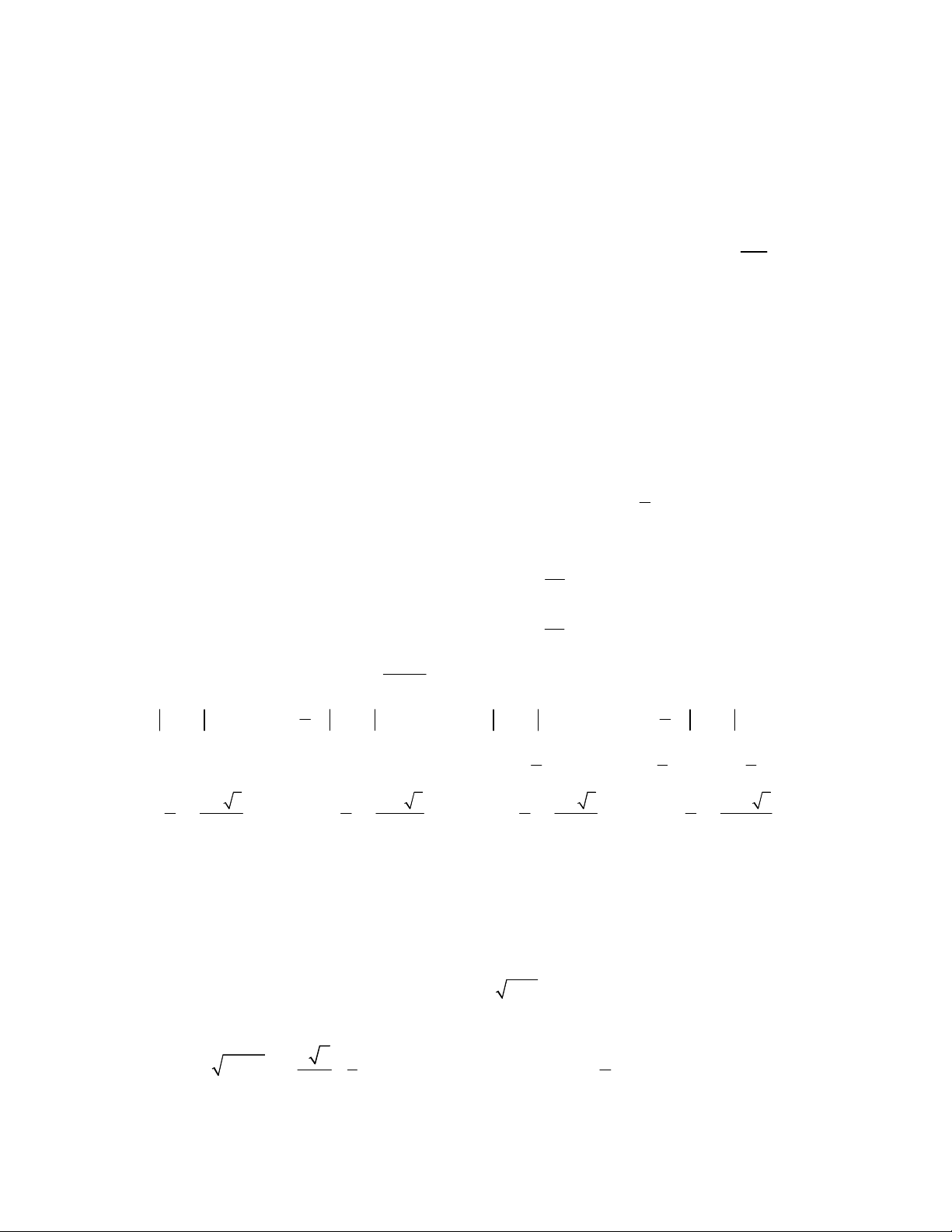(m2 )<br /> C.<br /> D.<br /> (m )<br /> (m )<br /> (m )<br /> 3<br /> 3<br /> 3<br /> 3<br /> <br /> Trang 3/5 - Mã đề thi 001<br /> <br /> TRƯỜNG THPT<br /> TRẦN NHẬT DUẬT<br /> <br /> ĐỀ KIỀM TRA 1 TIẾT<br /> CHƯỚNG III - GIẢI TÍCH 12<br /> Thời gian làm bài: 45 phút;<br /> Mã đề thi 001<br /> <br /> Câu 1. Khẳng định nào sau đây đúng<br /> B.  e2 x dx  e2 x  C<br /> <br /> A.  sin xdx  cosx  C<br /> <br /> C.  a 2 x dx  a 2 x .ln a  C<br /> <br /> Câu 2. Cho f (x ) liên tục trên đoạn  0;10 thỏa mãn<br /> 2<br /> <br /> <br /> <br /> 10<br /> <br /> 0<br /> <br /> D.  a x dx <br /> <br /> ax<br /> C<br /> ln a<br /> <br /> 6<br /> <br /> f ( x)dx  2017;  f ( x)dx  2016<br /> 2<br /> <br /> 10<br /> <br /> Khi đó giá trị của P   f (x )d x   f (x )d x là<br /> 0<br /> <br /> 6<br /> <br /> A. 1<br /> <br /> B. 1<br /> <br /> D. 2<br /> <br /> C. 0<br /> d<br /> <br /> Câu 2: Cho hàm f liên tục trên<br /> <br /> thỏa mãn<br /> <br /> <br /> <br /> d<br /> <br /> A. 2 xe x<br /> <br /> 2<br /> <br /> 1<br /> <br /> c<br /> <br /> f  x  dx  10,  f  x  dx  8,  f  x  dx  7 . Tính<br /> <br /> a<br /> <br /> A. -5 B. 7<br /> C. 5<br /> x 2 1<br /> Câu 3.  xe dx bằng:<br /> <br /> c<br /> <br /> b<br /> <br /> a<br /> <br />  f  x  dx<br /> b<br /> <br /> D. -7<br /> <br /> B. e x<br /> <br /> C<br /> <br /> 2<br /> <br /> 1<br /> <br />  C C. x 2e x<br /> <br /> 2<br /> <br /> 1<br /> <br /> C<br /> <br /> D.<br /> <br /> 1 x 2 1<br /> e<br /> C<br /> 2<br /> <br /> Câu 4. Hàm số F ( x )  e x  e  x  x là một nguyên hàm của hàm số<br /> x2<br /> 2<br /> x2<br /> C. f ( x)  e x  e x  1<br /> D. f  x   e x  e x <br /> 2<br /> 2<br /> Câu 5. Nguyên hàm của hàm số f ( x ) <br /> là<br /> 7x  3<br /> 1<br /> A. ln 7 x  3  C<br /> B. ln 7 x  3  C<br /> C. 2 ln 7 x  3  C<br /> 7<br /> <br /> B. f ( x)  e x  e x <br /> <br /> A. f ( x)  e  x  e x  1<br /> <br /> <br /> <br /> D.<br /> <br /> 2<br /> ln 7 x  3  C<br /> 7<br /> 2<br /> <br /> <br /> <br /> <br /> <br /> Câu 6. Biết F ( x) là một nguyên hàm của hàm số f ( x)  sin   3 x  và F (0)  . Tính F   .<br /> 3<br /> 3<br /> <br /> 2<br /> <br /> <br /> A. F   <br /> 2<br /> <br /> 5 3<br /> .<br /> 6<br /> <br />    1 3 3<br /> .<br /> 6<br /> <br /> <br /> <br /> B. F   <br /> 2<br /> <br /> C. F   <br /> 2<br /> <br /> 3 3<br /> .<br /> 6<br /> <br /> <br /> <br /> D. F   <br /> 2<br /> <br /> 73 3<br /> .<br /> 6<br /> <br /> Câu 7.Tính I   x sin xdx , đặt u  x , dv  sin xdx . Khi đó I biến đổi thành<br /> A. I   x cos x   cos xdx<br /> C. I  x cos x   cos xdx<br /> <br /> B. I   x cos x   cos xdx<br /> D. I   x sin x   cos xdx<br /> 8<br /> <br /> Câu 8. Cho hàm số f ( x) liên tục trên  1;   và<br /> <br /> <br /> 0<br /> <br /> 3<br /> <br /> f ( x  1) dx  10 Tính I   x. f ( x)dx<br /> 1<br /> <br /> A. I = 5 .<br /> <br /> B. I = 10 .<br /> C. I = 20 .<br /> D. I = 40 .<br /> 1<br /> a 2 c<br /> a<br /> 2<br />  trong đó a, b, c nguyên dương và<br /> là phân số tối giản.<br /> Câu 9. Biết  x 2  x dx <br /> b<br /> 3<br /> b<br /> 0<br /> Tính M  log 2 a  log3 b  c 2<br /> A.2.<br /> B. 3.<br /> <br /> C. 5 .<br /> <br /> D. 4 .<br /> <br /> Trang 4/5 - Mã đề thi 001<br /> <br /> 1<br /> <br /> Câu 10. Cho<br /> <br /> <br /> <br /> ( x  1) d x<br /> x2  2x  2<br /> <br /> 0<br /> <br /> A. 1 .<br /> <br />  a  b . Tính a  b<br /> B. 5 .<br /> <br /> 5<br /> <br /> Câu 11. Cho<br /> <br /> x<br /> 2<br /> <br /> A. 18 .<br /> <br /> C. 2 .<br /> <br /> D. 3 .<br /> <br /> dx<br />  a ln 2  b ln 5 với a, b là hai số nguyên. Tính M  a 2  2ab  3b 2<br /> x<br /> B. 6 .<br /> C. 2 .<br /> D. 11 .<br /> <br /> 2<br /> <br /> Câu 12. Biết tích phân<br /> <br /> 1<br /> <br /> x<br /> <br />   x  3 e dx  a  be với a, b <br /> 0<br /> <br /> B. a  b  25.<br /> <br /> A. a  b  1.<br /> x<br /> 4<br /> <br /> Câu 13. Cho I   x tan 2 xdx <br /> <br /> <br /> <br /> . Tìm tổng a  b .<br /> <br /> C. a  b  4  3e.<br /> <br /> D. a  b  1 .<br /> <br /> 2<br /> <br /> khi đó tổng a  b bằng<br /> 32<br /> A. 4.<br /> B. 8.<br /> C. 10.<br /> D. 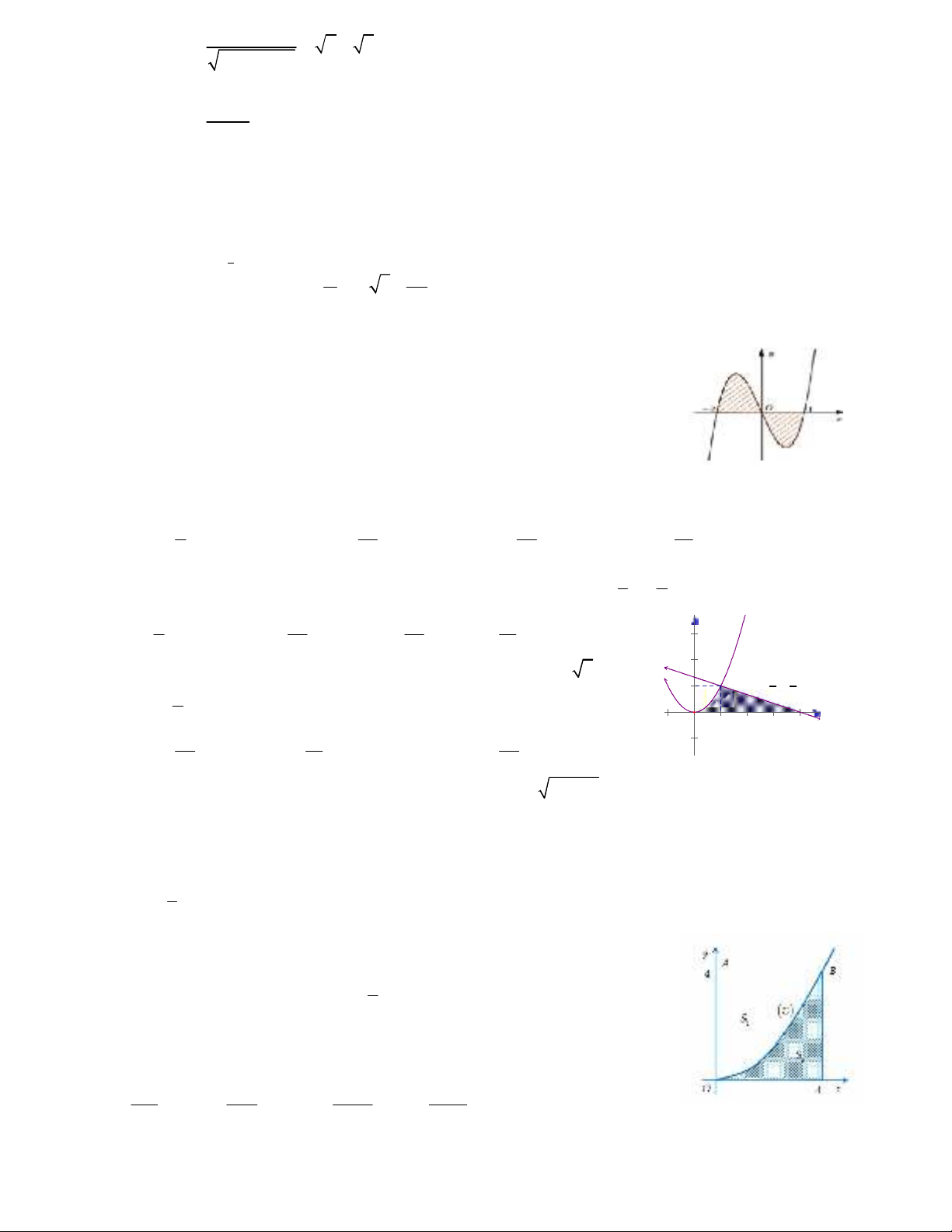6.<br /> Câu 14. Cho hàm số y = f ( x) có đồ thị như hình vẽ.<br /> Diện tích hình phẳng phần tô đậm trong hình là<br /> a<br /> <br /> 0<br /> <br />  ln b <br /> <br /> 1<br /> <br /> A. S <br /> <br /> <br /> <br /> 0<br /> <br /> 1<br /> <br /> <br /> <br /> f ( x) dx   f ( x) dx .<br /> <br /> 2<br /> <br /> 2<br /> 2<br /> <br /> C. S <br /> <br /> B. S <br /> <br /> f ( x)dx .<br /> 1<br /> <br />  f ( x)dx   f ( x)dx .<br /> 0<br /> <br /> 0<br /> <br /> 0<br /> <br /> D. S <br /> <br /> 0<br /> <br /> 1<br /> <br />  f ( x)dx   f ( x)dx .<br /> 2<br /> <br /> 0<br /> <br /> Câu 15. Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y  x3  x và y  x  x 2<br /> A.<br /> <br /> 8<br /> .<br /> 3<br /> <br /> B.<br /> <br /> 33<br /> .<br /> 12<br /> <br /> C.<br /> <br /> 37<br /> .<br /> 12<br /> <br /> D.<br /> <br /> 5<br /> .<br /> 12<br /> <br /> 1<br /> 4<br /> Câu 16. Tính diện tích hình phẳng giới hạn bởi các đường y  x 2 , y   x  và trục hoành như hình vẽ.<br /> 3<br /> 3<br /> y<br /> 7<br /> 56<br /> 39<br /> 11<br /> A. .<br /> B.<br /> .<br /> C.<br /> .<br /> D.<br /> .<br /> y = x2<br /> 3<br /> 3<br /> 2<br /> 6<br /> 2<br /> Câu 17. Kí hiệu (H) là hình phẳng giới hạn bởi đồ thị hàm số y  3 x  x và<br /> đường<br /> 1<br /> 4<br /> 1<br /> y = - x+<br /> 3<br /> 3<br /> 1<br /> x<br /> thẳng y  x . Tính diện tích hình (H).<br /> 4<br /> O<br /> 2<br /> 1<br /> 57<br /> 13<br /> 25<br /> A.<br /> .<br /> B.<br /> .<br /> C. 4 .<br /> D.<br /> .<br /> 5<br /> 2<br /> 4<br /> <br /> Câu 18. Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số y  4 x  e x , trục hoành và hai đường thẳng<br /> x  1; x  2 . Tính thể tích V của khối tròn xoay thu được khi quay hình (H) xung quanh trục hoành.<br /> A. V   (6  e2 ) .<br /> B. V   (6  e  e2 ) C. V   (6  e  e2 ) .<br /> D V   (6  2e  e2 )<br /> Câu 19: Một ô tô đang chạy với vận tốc 36 km / h thì tăng tốc chuyển động nhanh dần đều vơi gia tốc<br /> t<br /> a (t )  1  ( m / s 2 ) . Tính quãng đường mà ô tô đi được sau 6s kể từ khi bắt đầu tăng tốc.<br /> 3<br /> A. 58m<br /> B. 90m<br /> C. 100m<br /> D. 246m<br /> Câu 20. Hình vuông OABC có cạnh bằng 4 được chia thành hai phần bởi<br /> 1<br /> 4<br /> <br /> đường cong  C  có phương trình y  x 2 . Gọi S1 là diện tích của phần không<br /> <br /> bị<br /> <br /> gạch (như hình vẽ). Tính thể tích khối tròn xoay khi cho phần S1 quay quanh<br /> trục Ox ta được.<br /> A.<br /> <br /> 128<br /> .<br /> 3<br /> <br /> B.<br /> <br /> 64<br /> .<br /> 3<br /> <br /> C.<br /> <br /> 256<br /> .<br /> 5<br /> <br /> D<br /> <br /> 128<br /> 3<br /> <br /> Trang 5/5 - Mã đề thi 001<br /> <br />