SỞ GIÁO DỤC VÀ ĐÀO TẠO TP. HCM
TRƯỜNG THPT BÌNH CHIỂU

KIỂM TRA GIỮA HKI – NĂM HỌC 2022 – 2023
Môn thi: TOÁN - KHỐI 11
Ngày thi: 27/10/2022
Thời gian: 60 phút, không kể thời gian phát đề
MÃ ĐỀ 111
Câu 1 (1 điểm): Tìm tập xác định của hàm số lượng giác:
sin2
cos 1
x
yx
.
Câu 2 (1 điểm): Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số lượng giác:
2 3sin 6
yx



.
Câu 3 (6 điểm): Giải các phương trình lượng giác sau:
a)
00
sin 30 sin45x
. b)
3sin cos 2xx
.
c)
2
2sin 7sin 3 0xx
. d)
.
e)
22
3sin sin cos 2cos 1x x x x
. f)
2
2
11
cos 2 cos 2 0
cos cos
xx
xx



.
Câu 4 (1 điểm): Trong mặt phẳng tọa độ Oxy cho vectơ
1, 2u
, tìm ảnh của điểm A(4; -3) qua
phép tịnh tiến vectơ
u
.
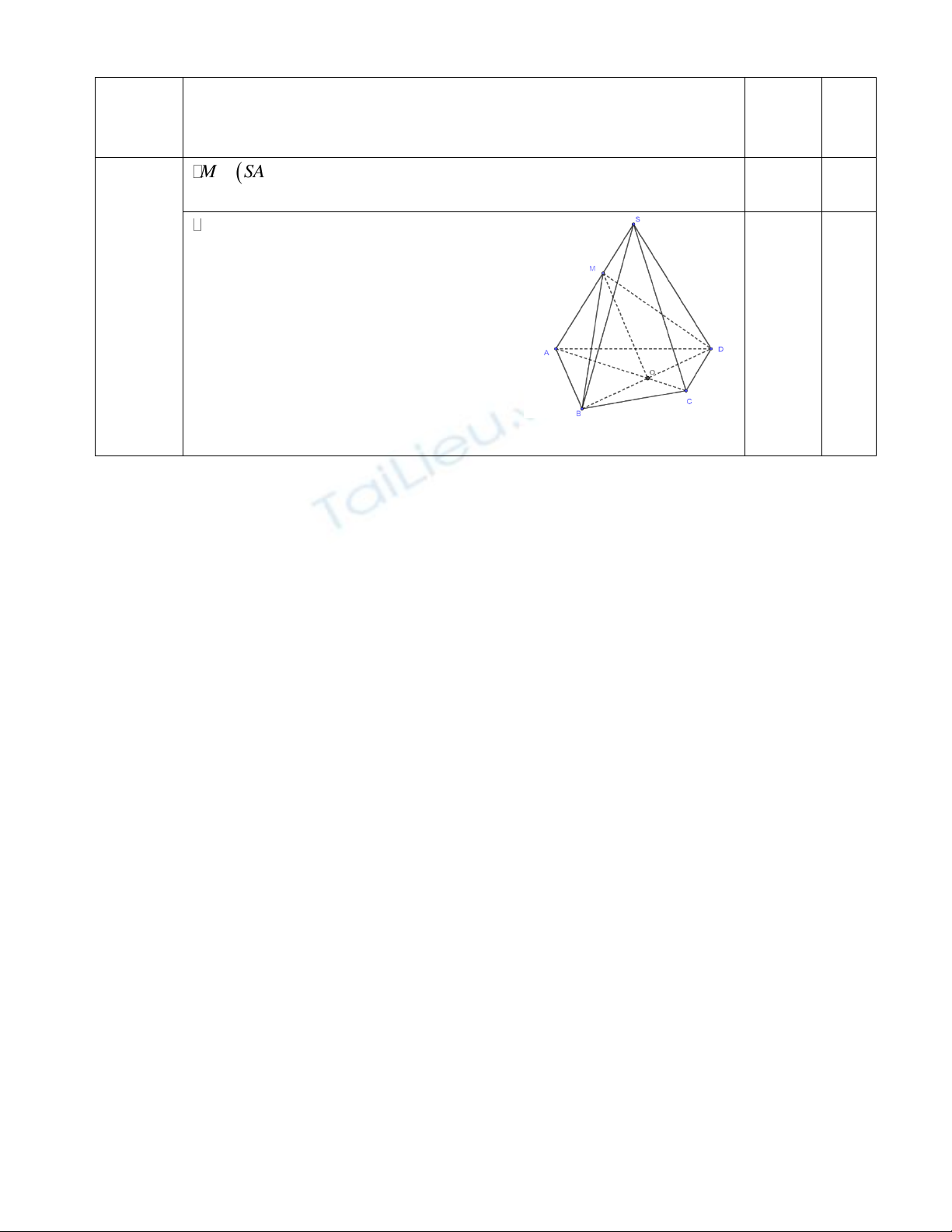
Câu 5 (1 điểm): Cho hình chóp S. ABCD, đáy ABCD là tứ giác có các cặp cạnh đối không song song,
điểm M thuộc cạnh SA. Tìm giao tuyến của mặt phẳng (SAC) và (MBD).
--- HẾT ---
Học sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ và tên thí sinh: ………………………………………Số báo danh: …………………………..…...
Chữ kí giám thị 1: ………………………………………. Chữ kí giám thị 2: ………………………….
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP. HCM
TRƯỜNG THPT BÌNH CHIỂU

KIỂM TRA GIỮA HKI – NĂM HỌC 2022 – 2023
Môn thi: TOÁN - KHỐI 11
Thời gian: 60 phút, không kể thời gian phát đề
ĐÁP ÁN MÃ ĐỀ 111
Câu hỏi
Điểm
Ghi
chú
Câu 1
1 điểm
ĐKXĐ:
cos 1 0x
cos 1x
2xk

kZ
0.25x3
Vậy TXĐ:
\ 2 ,D R k k Z

.
0.25
Câu 2
1 điểm
1 sin 1
6
x



3 3sin 3
6
x



15y
.
0.25x2
GTLN y = 5 khi
sin 1
6
x




2
3
xk
kZ
.
0.25
GTNN y = -1 khi
sin 1
6
x



22
3
xk
kZ
.
0.25
Câu 3
a)
1 điểm
00
sin 30 sin45x
0 0 0
0 0 0 0
30 45 360
30 180 45 360
xk
xk
00
00
75 360
165 360
xk
xk


kZ
.
0.5x2
b)
1 điểm
3sin cos 2xx
3 1 2
sin cos
2 2 2
xx
2
sin 62
x



0.25x2
2
64
2
64
xk
xk



2
12
72
12
xk
xk


kZ
.
0.25x2
c)
1 điểm
2
2sin 7sin 3 0xx
sin 3 (ptvn)
1
sin 2
x
x
2
6
52
6
xk
xk


kZ
0.5x2
d)
1 điểm
2
4cos 12cos 5 0xx
0.25
1
cos 2
5
cos (ptvn)
2
x
x


22
3
xk
kZ
.
0.25x3
e)
1 điểm
22
3sin sin cos 2cos 1x x x x
(*)
TH1: cos x = 0
2
xk
kZ
.
(*)
31
(vô lí). Vậy
2
xk
kZ
không là nghiệm của (*).
0.25
TH2: cos x ≠ 0
2
xk
kZ
.
(*)
2
2tan tan 3 0xx
tan 1
3
tan 2
x
x

n
43
arctan n
2
xk
xk

0.25x3
f)
1 điểm
2
2
11
cos 2 cos 2 0
cos cos
xx
xx



(*) ĐK:
cos 0x
.
Đặt
1
cos cos
txx

, khi đó:
2
(*) 2 0tt
02tt
0.5
0t
2
cos 1 0x
(ptvn).
0.25
2t
2
cos 2cos 1 0xx
cos 1 (n)x
2 .x k k Z
0.25
Câu 4
1 điểm
Gọi A’(x’; y’) là ảnh của A qua phép tịnh tiến vectơ
u
.
0.5x2
'
'
x x a
y y b


'5
'5
x
y

. Vậy A’(5; -5).
Câu 5
1 điểm
M SAC MBD
(1)
0.25
Trong (ABCD) gọi
O AC BD
khi đó:
O AC SAC
O BD SBD


O SAC MBD
(2)
Từ (1), (2) suy ra
MO SAC MBD
.
0.25
0.25
0.25
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP. HCM
TRƯỜNG THPT BÌNH CHIỂU

KIỂM TRA GIỮA HKI – NĂM HỌC 2022 – 2023
Môn thi: TOÁN - KHỐI 11
Ngày thi: 27/10/2022
Thời gian: 60 phút, không kể thời gian phát đề
MÃ ĐỀ 112
Câu 1 (1 điểm): Tìm tập xác định của hàm số lượng giác:
cos2
sin 1
x
yx
.
Câu 2 (1 điểm): Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số lượng giác:
5 2cos 3
yx



.
Câu 3 (6 điểm): Giải các phương trình lượng giác sau:
a)
00
cos 45 cos30x
. b)
sin 3cos 2xx
.
c)
2
2cos 3cos 2 0xx
. d)
2
6cos 5sin 2 0xx
.
e)
22
5sin 2sin cos cos 2x x x x
. f)
2
2
42
2 sin 9 sin 1
sin sin
xx
xx
.
Câu 4 (1 điểm): Trong mặt phẳng tọa độ Oxy cho vectơ
2,1v
, tìm ảnh của điểm A(2; -5) qua
phép tịnh tiến vectơ
v
.
Câu 5 (1 điểm): Cho hình chóp S.ABCD, đáy ABCD là tứ giác có các cặp cạnh đối không song song,
điểm M thuộc cạnh SA. Tìm giao tuyến của mặt phẳng (MBC) và (SAD).
--- HẾT ---
Học sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ và tên thí sinh: ………………………………………Số báo danh: …………………………..…...
Chữ kí giám thị 1: ………………………………………. Chữ kí giám thị 2: ………………………….