Khoa Ñieän ÑEÀ KIEÅM TRA GIÖÕA KYØ MOÂN TRÖÔØNG ÑIEÄN TÖØ – CQ10 (Ngaøy 28-10-2011)
BMCSKTÑieän ------ Thôøi gian 75 phuùt , khoâng keå cheùp ñeà -----------
Baøi 1: Töø phöông trình luaät Faraday daïng tích phaân, haõy daãn ra daïng vi phaân cuûa luaät naøy.
Baøi 2: Maët phaúng 4x – 5z = 0 chia khoâng gian thaønh 2 mieàn. Mieàn 1 (4x – 5z < 0) coù µ1 = 5µ0 . Mieàn 2 (4x – 5z
> 0) coù µ2 = 10µ0. Bieát treân bieân toàn taïi doøng maët Sy
J35a A/m=
G
G
vaø tröôøng töø veà phía moâi tröôøng 1 laø :
1xyz
H 25a 30a 45a A/m=−+
GGGG . Tìm tröôøng töø treân bieân veà phía moâi tröôøng 2: 2
H
G
?
Baøi 3: Trong moâi tröôøng ñieän moâi lyù töôûng (σ = 0, ε = εrε0, µ = µ0) tồn tại tröôøng töø
8
y
H 25sin(2.10 t 6 )a mA/mx=+
GG. Duøng heä phöông trình Maxwell, xaùc ñònh ñoä thaåm ñieän töông ñoái εr vaø
tröôøng ñieän E
G gắn với trường töø treân ?
Baøi 4: Cho ε = ε0 vaø phaân boá ñieän tích khoái ρV = 4r2 nC/m3 toàn taïi trong mieàn voû truï daøi voâ haïn, 1m < r < 2m.
Bieát ρV = 0 ôû caùc mieàn coøn laïi. (a) Tìm vectô caûm öùng ñieän ôû caùc mieàn ? (b) Xaùc ñònh naêng löôïng tröôøng ñieän
tích luõy beân trong khoái truï baùn kính 3m, cao 4m vaø taâm taïi goác toïa ñoä ?
Baøi 5: Tuï ñieän caàu, baùn kính coát tuï trong laø a, baùn kính coát tuï ngoaøi laø b, caùch ñieän laø ñieän moâi lyù töôûng coù ñoä
thaåm ñieän ε = 10ε0/r , r = baùn kính höôùng taâm. Coát tuï trong coù theá ñieän U = const, coát tuï ngoaøi noái ñaát. (a) Tìm
caûm öùng ñieän, cöôøng ñoä tröôøng ñieän vaø theá ñieän trong ñieän moâi ? (b) Tìm maät ñoä ñieän tích maët treân beà maët coát
tuï trong ? (c) Tìm ñieän dung C cuûa tuï ?
-------------------------------- Boä moân duyeät
♦ Sinh vieân khoâng ñöôïc söû duïng taøi lieäu - Caùn boä coi thi khoâng giaûi thích ñeà thi .
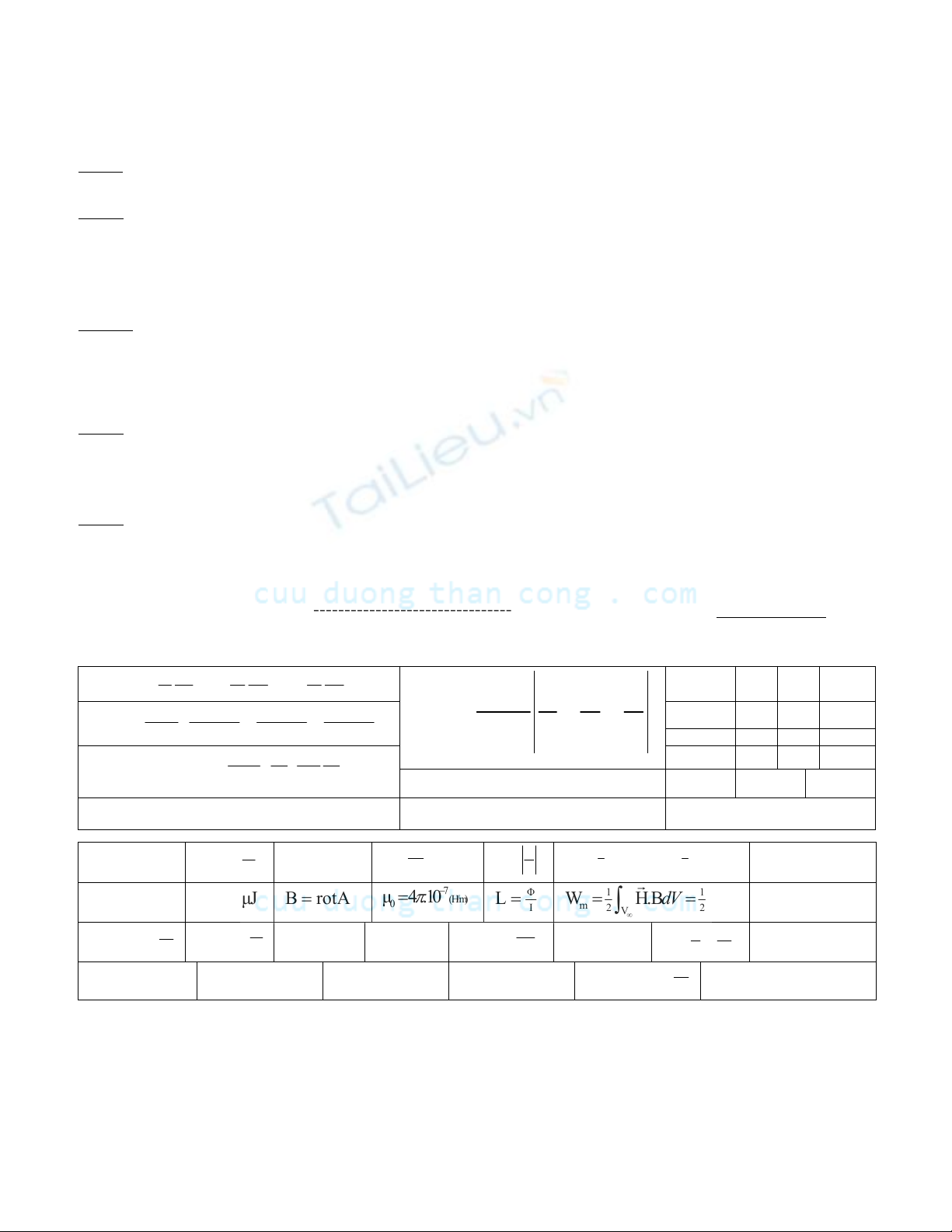
♦ Moät soá coâng thöùc cô baûn coù theå tham khaûo:
11 2 2 3 3
11 1
123
hh h
grad a a a
uu u
ϕϕ ϕ
ϕ
∂∂ ∂
∂∂ ∂
=+ +
GGG
Heä h1 h
2 h
3
Ñeà caùc 1 1 1
23 1 13 2 12 3
123 1 2 3
(h h A ) (h h A ) (h h A )
1
hh h u u u
divA ∂∂∂
∂∂∂

=++

G Truï 1 r 1
11 2 2 3 3
12 3
11 2 2 3 3
ha h a ha
uu u
123
hA h A hA
1
rotA hh h
∂
∂∂
∂∂ ∂
=
G
GG
G
Caàu 1 r rsinθ
(
)
23
123 1 1 1
hh
1
hh h h
div(grad ) ...
uu
ϕ
ϕϕ
∂∂
∂∂

∆= = +

A grad(divA) rot(rotA)∆= −
G
GG
DεE=
GG
BµH=
GG
JE
σ
=
G
G
23 2 31 13 1 32 12 1 23
hh a hh a hh adS du du du du du du=± ± ±
GGG G
111 2 22 3 33
hah ah addu du du=+ +
G
GG
A 123 1 2 3
hhhdV du du du=
DS
sdq
∗
=
∫G
G
v V
ρ
ε
ϕ
∆=− Egrad
ϕ
=−
G
19(F/m)
036
ε10
π
−
= Q
U
C
=
11
2
e22
V
WE.DC.UdV
∞
==
∫
G
G ECdl
ϕ
=
−+
∫
G
G
HI
Ld∗
=
∫G
G
A
v AµJ∆=−
GG BrotA=G
G 7(H/m)
0
µ4.10
π
−
= Φ
I
L
=
11
2
m22
V
WH.BL.IdV
∞
==
∫
G
G 0
P(εε)E=−
GG
D
t
rotH J ∂
∂
=+
G
GG B
t
rotE ∂
∂
=−
G
G V
divD ρ=
G divB 0
=
G
V
ρ
t
divJ ∂
∂
=
−
G
JV
PEJdV=∫
G
G 2
J
UU
IP
R== pV
ρdivP=−
G
n12s
a(HH)J×− =
GG G
G n12
a(EE)0×− =
GG
G n1 2 S
a.(D D) ρ−=
GG
G n1 2
a.(B B) 0
−
=
G
G
G
S
ρ
n1 2 t
a.(J J) ∂
∂
−
=−
G
G
G
p
Sn12
a(P P)
ρ
=− −
G
G
G
CuuDuongThanCong.com https://fb.com/tailieudientucntt