PHÒNG GIÁO D C VÀ ĐÀO T OỤ Ạ
QU N TÂN BÌNHẬ
Đ KI M TRA H C KỲ II NĂM H C 2011 - 2012Ề Ể Ọ Ọ
MÔN TOÁN - L P 9Ớ
Th i gian làm bài: 90 phút ( không k th i gian phát đ )ờ ể ờ ề
Bài 1: Gi i ph ng trình và h ph ng trình sau : ả ươ ệ ươ
a)
2
4x 5x 6 0+ − =
(1đ)
b)
4 2
5 6 0x x− − =
(1đ)
c)
3 10
5 3 6
x y
x y
− =
− =
(1đ)
Bài 2: Cho parabol (P) :
2
2
x
y=
và đ ng th ng (d) : ườ ẳ
4y x= +
a) V (P) trên m t ph ng t a đ . (1đ)ẽ ặ ẳ ọ ộ
b) Xác đ nh t a đ các giao đi m c a (P) và (d) b ng phép tinh. (0.75đ)ị ọ ộ ể ủ ằ
Bài 3: Cho ph ng trình:ươ
2
x (m 3)x 3m 0+ − − =
(x là n s )ẩ ố
a) Ch ng minh ph ng trình trên luôn có nghi m v i m i giá tr c a m. (0.75đ)ứ ươ ệ ớ ọ ị ủ
b) Tìm t ng và tích hai nghi m c a ph ng trình trên theo m (0.5đ)ổ ệ ủ ươ
c) G i ọ
1 2
x , x
là hai nghi m c a ph ng trình. Tìm m đđ : ệ ủ ươ ể
(0.5đ)
Bài 4: Cho đ ng tròn (O) đ ng kính AB = 2R. T A v ti p tuy n Ax v i (O) ( Aườ ườ ừ ẽ ế ế ớ
là ti p đi m). Trên tia Ax l y đi m C sao cho AC = 2R. Qua C v đ ng th ng c t đ ngế ể ấ ể ẽ ườ ẳ ắ ườ
tròn (O) t i hai đi m D và E ( D n m gi a C và E; đ ng th ng này cũng c t đo n th ngạ ể ằ ữ ườ ẳ ắ ạ ẳ
OB). G i H là trung đi m đo n th ng DEọ ể ạ ẳ
a) Ch ng minh: ứ
2
CA CD CE=
(1đ)
b) Ch ng minh: t giác AOHC n i ti p (1đ)ứ ứ ộ ế
c) Đo n th ng CB c t đ ng tròn (O) t i K. Tính s đo góc AOK và di n tích hìnhạ ẳ ắ ườ ạ ố ệ
qu t AOK theo R và ð (1đ)ạ
d) Đ ng th ng CO c t tia BD, tia BE l n l t t i M và N. Ch ng minh: O là trungườ ẳ ắ ầ ượ ạ ứ
đi m đo n th ng MN. (0.5đ)ể ạ ẳ
H TẾ
Đ CHÍNH TH CỀ Ứ
H NG D N ĐÁP ÁN MÔN TOÁN - L P 9 – HKII 11-12ƯỚ Ẫ Ớ
Bài 1: Gi i các ph ng trình :ả ươ
a)
2
4x 5x 6 0+ − =
(
a 4
=
;
b 5
=
;
c 6
= −
)
( )
2 2
b 4ac 5 4 4 6 25 96 121 0 (0,5đ)
11
∆ = − = − − = + = >��
∆ =
Vì
0∆ >
nên ph ng trên có 2 nghi m phân bi t:ươ ệ ệ
1
2
b 5 11 6 3
x (0,25đ)
2a 2 4 8 4
b 5 11 16
x 2 (0,25đ)
2a 2 4 8
− + ∆ − +
= = = =
− − ∆ − − −
= = = = −
b)
4 2
5 6 0x x− − =
Đ t ặ
0
2≥= xt
Ta đ c: ượ
2
5 6 0t t− − =
(0,25đ)
Gi i ra ta đ c : ả ượ
1
1−=t
( lo i) ; ạ
2
6t=
(nh n) ậ
(0,25đ)
V i ớ
6t=
thì
2
6x=
6x=� �
V y ph ng trình ban đ u có 2 nghi m: ậ ươ ầ ệ
6x=
(0,5đ)
c)
3 10
5 3 6
x y
x y
− =
− =
( )
3 10
5 3 3 10 6
y x
x x
= −
− − =
⇔
. . . . . . . . . . . . . . .
6 (0,5đ)
8 (0,5đ)
x
y
=
=
V y : ( x = 6 ; y = 8 )ậ
Bài 2:
a) (P) :
2
2
1xy =
L p b ng giá tr đúng (0.5đ)ậ ả ị
x -2 -1 0 1 2
2
2
1xy =
2
2
1
0
2
1
2
V đúng (P) (0.5đ) ẽ
b) (P) :
2
2
1xy =
(d) :
4y x= +
Ph ng trình hoành đ giao đi m gi a (P) và (d) là: ươ ộ ể ữ
2
14
2x x= +
(0.25đ)
Gi i ra ta tìm đ c : t a đ giao đi m gi a (P) và (d) là: (-2; 2) và (4; 8) (0.5đ)ả ượ ọ ộ ể ữ
Bài 3 : Cho ph ng trình :ươ
2
x (m 3)x 3m 0+ − − =
a) (
a 1
=
;
b m 3
= −
;
c 3m
= −
)
Ta có :
( )
2 2 2
b 4ac (m 3) 4 1 3m m 6m 9 12m∆ = − = − − − = − + +��
2 2
m 6m 9 (m 3) 0; m= + + = + ∀
(0,5đ)
V y ph ng trình luôn có nghi m v i m i giá tr c a m. (0.25đ)ậ ươ ệ ớ ọ ị ủ
b) Tính t ng và tích c a hai nghi m theo m.ổ ủ ệ
Ta có :
( )
1 2
b
S x x m 3
a
−
= + = = − −
(0.25đ)
1 2
c
P x .x 3m
a
= = = −
(0.25đ)
c) Ta có :
2 2
1 2 1 2
x x x .x 9+ − =�
2
1 2 1 2 1 2
2
1 2 1 2
(x x ) 2x .x x .x 9
(x x ) 3x .x 9
+ − − =�
+ − =�
Thay
1 2
x x m 3+ = −
và
1 2
x .x 3m= −
Ta có:
[ ]
( )
2
(m 3) 3 3m 9− − − − =�
2
2
2
(m 3) 9m 9
m 6m 9 9m 9
m 3m 0
− + =�
− + + =�
+ =�
Gi i ra ta đ c: ả ượ
0m=
;
3m= −
(0,5đ)
V y: ………ậ
Bài 4:
a) Ch ng minh ứ∆CDA ∼ ∆CAE (g-g)
CD CA
CA CE
=�
⇒
2
CA CD CE=
(1đ)
b) Ch ng minhứ
ﾷ
0
90CHO =
Xét t giác AOHC có :ứ
ﾷ
0
90CHO =
( cmt)
ﾷ
0
90CAO =
( T/c ti p tuy n)ế ế
⇒
ﾷ
ﾷ
0
180CHO CAO+ =
⇒ T giác AOHC n i ti pứ ộ ế
( t ng hai góc đ i di n b ng 180ổ ố ệ ằ 0) (1đ)
c) Sđ
ﾷ
0
90AOK =
(0.5đ)
Squ tAOKạ =
2 2
90
360 4
R R
π π
=
( đvdt) (0.5đ)
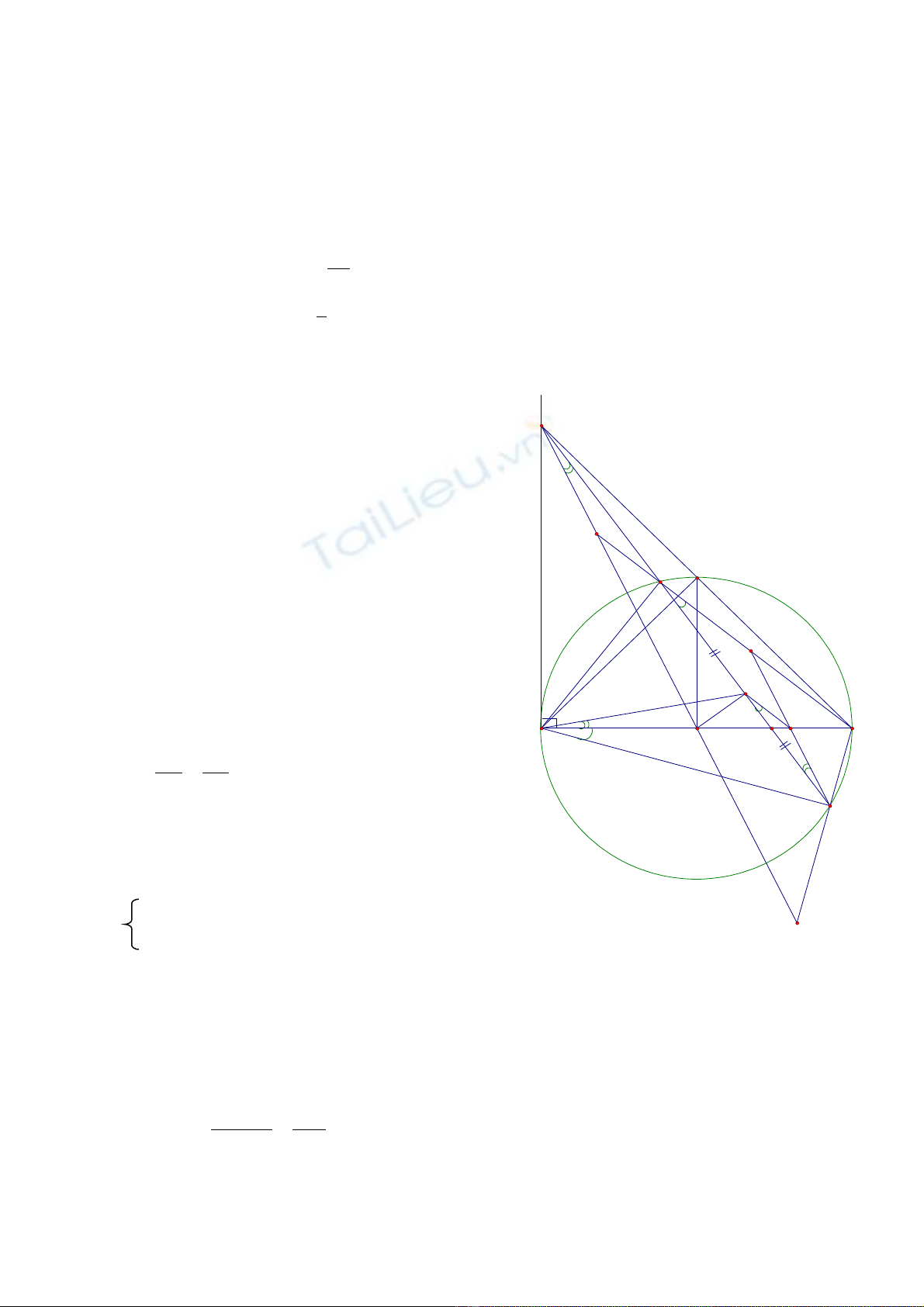
d) T E v đ ng th ng song song v i MN c t c nh AB t i I và c t c nh BD t i F. ừ ẽ ườ ẳ ớ ắ ạ ạ ắ ạ ạ
Vì t giác AOHC n i ti p (cmt)ứ ộ ế
x
F
I
K
N
M
H
E
D
O
AB
C
⇒
ﾷ
ﾷ
HAO HCO=
Mà
ﾷ
ﾷ
HEI HCO=
(So le trong, EF//MN)
⇒
ﾷ
ﾷ
HAO HEI=
Hay
ﾷ ﾷ
IAH IEH=
⇒ t giác AHIE n i ti p ( 2 đ nh k nhau cùng nhìn c nh HI d i góc b ng nhau)ứ ộ ế ỉ ề ạ ướ ằ
⇒
ﾷ
ﾷ
IHE IAE=
Mà
ﾷ
ﾷ
IAE BDE=
(2 góc n i ti p cùng ch n cung BE)ộ ế ắ
⇒
ﾷ
ﾷ
IHE BDE=
Mà 2 góc này v trí đ ng vở ị ồ ị
⇒ HI // BD
Ch ng minh I là trung đi m EFứ ể
Xét ∆BMO có IF // OM (EF//MM)
⇒
IF BI
OM BO
=
(1) (H qu Talet)ệ ả
Xét ∆BNO có IE // ON (EF//MM)
⇒
IE BI
ON BO
=
(2) (H qu Talet)ệ ả
T (1) và (2) suy ra: ừ
IF IE
OM ON
=
Mà IE = IF (I là trung đi m EF)ể
⇒ OM = ON
Mà
O MN
⇒ O là trung đi m đo n th ng MN (0.5đ)ể ạ ẳ
H TẾ