SỞ GIÁO DỤC VÀ ĐÀO
TẠO KIỂM TRA CHẤT LƯỢNG HỌC KỲ I
ĐỒNG THÁP Năm học: 2012 – 2013
Môn thi: TOÁN – LỚP 12
ĐỀ ĐỀ XUẤT Thời gian: 90 phút (không kể thời gian phát đề)
(Đề gồm có 01 trang) Ngày thi: 20/12/2012
Đơn vị ra đề: THPT Cao
Lãnh 2
I. PHẦN CHUNG CHO TẤT CẢ THÍ SINH (7.0 điểm)
Câu 1 (3.0 điểm) Cho hàm số
2
( )
2
x
y x C
x
1) Khảo sát và vẽ đồ thị (C)
2) Đường thẳng
: 7 10
y x
cắt (C) tại 2 điểm A, B phân biệt. Tính độ
dài AB.
Câu 2 (2.0 điểm)
1) Tính giá trị biểu thức 2
3 log 3
1
3
2 3log 27
P
2) Tìm GTLN, GTNN của các hàm số
2
2 ln
y f x x x
trên đoạn 1
;
e
e
Câu 3.(2.0 điểm) Cho khối chóp S.ABC biết SA vuông góc với mp(ABC), góc
giữa SC và mặt đáy bằng
0
30
;
ABC
vuông tại A có
3
AC a
,
฀
0
60
ACB
1) Tính thể tích khối chóp S.ABC
2) Xác định tâm và tính bán kính mặt cầu ngoại tiếp khối chóp S.ABC
II. PHẦN RIÊNG – PHẦN TỰ CHỌN (3.0 điểm)
Học sinh chỉ được chọn một trong hai phần (phần 1 hoặc phần 2)
Phần 1: Theo chương trình chuẩn
Câu 5.a (1.0 điểm) Viết phương trình tiếp tuyến của
3 2
1
2 3 ( )
3
y f x x x x C
tại điểm có hoành độ
0
x
biết
0
" 0
f x
Câu 6.a (2.0 điểm) Giải phương trình, bất phương trình:
1) 1
4 33.2 8 0
x x
2) 4 1
2
2log ( 1) 1 log
x x
Phần 2: Theo chương trình nâng cao
Câu 5.b (1.0 điểm) Viết phương trình tiếp tuyến của
23 2
( )
2
x x
y f x C
x
tại
giao điểm của (C) và trục Ox.
Câu 6.b (2.0 điểm)
1) Cho hàm số
1
ln
1
y
x
. Chứng minh 2
1 2 '
y
e xy
2) Tìm m để đồ thị hàm số 2
( 1)( 2 6)
y x x mx m cắt trục hoành tại ba
điểm phân biệt
Hết./.
Học sinh không được sử dụng tài liệu. Giáo viên coi thi không giải thích gì
thêm.
Họ và tên học sinh: ……………………………………………; Số báo
danh:…………………
SỞ GIÁO DỤC VÀ ĐÀO
TẠO
KIỂM TRA CHẤT LƯỢNG HỌC KỲ I
ĐỒNG THÁP Năm học: 2012 – 2013
Môn thi: TOÁN – LỚP 12
HƯỚNG DẪN CHẤM ĐỀ ĐỀ XUẤT
(Hướng dẫn chấm gồm có 5 trang)
Đơn vị ra đề: THPT Cao Lãnh 2
CÂU NỘI DUNG YÊU CẦU ĐIỂM
Câu 1 Cho hàm số
2
( )
2
x
y x C
x
(3.0 điểm)
1) Khảo sát và vẽ đồ thị (C) (2.0 điểm)
* Tập xác định:
\{ 2}
D
฀
*
2
4
' 0,
2
y x D
x
* Tiệm cận ngang: y= –1 vì
lim 1; lim 1
x x
y y
 
* Tiệm cận đứng x= –2 vì
2 2
lim ; lim
x x
y y
 
* Bảng biến thiên:
x -
–2
+
y
’
– –
y –1
+
0,25
0,25
0,25
0,25
0, 5
–
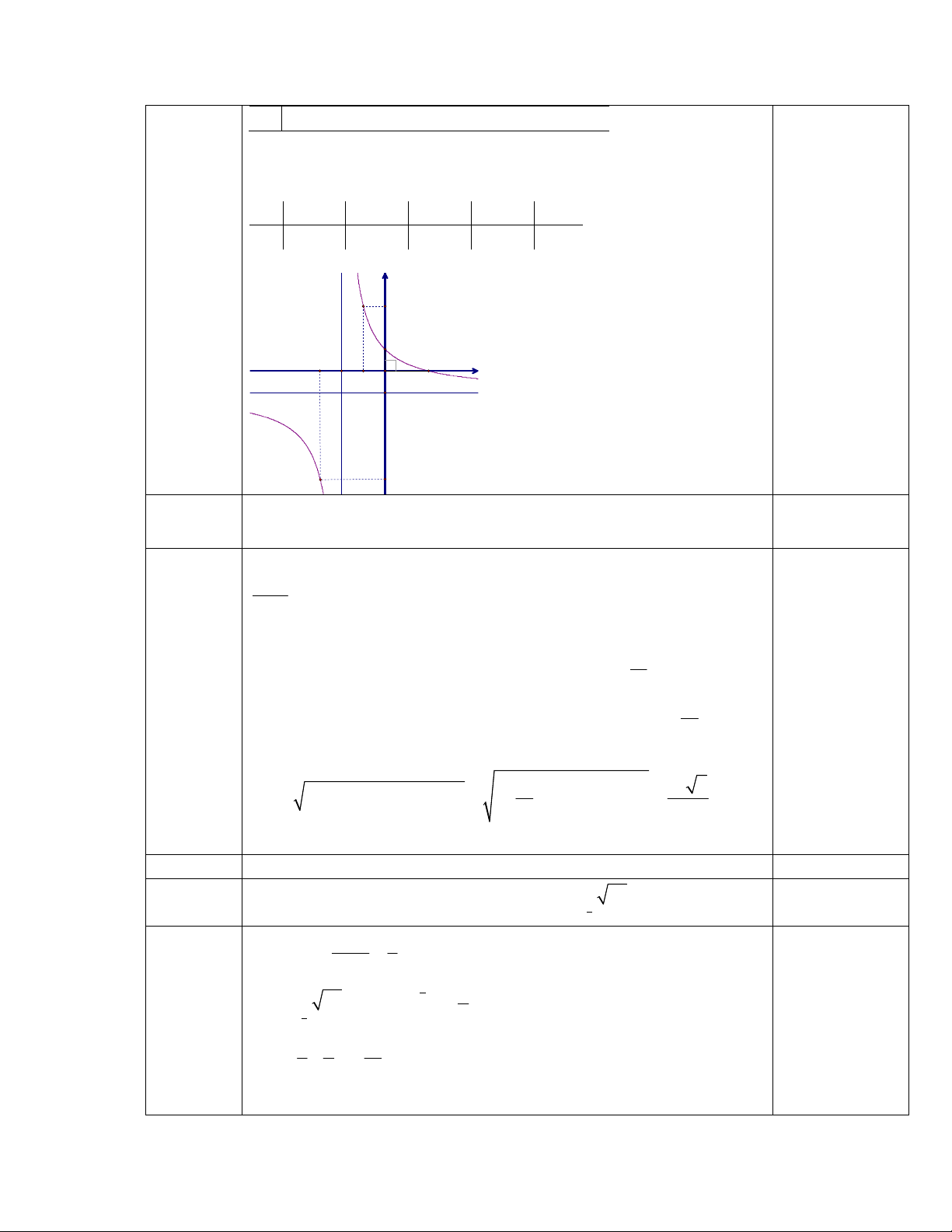
–1
Hàm số nghịch biến trên: (–
;–2), (–2;+
)
Hàm số không có cực trị
* Điểm đặc biệt:
x
-6 –4 –2 0 2
y -2 –3 kxd 1 0
* Đồ thị:
x
y
y=-1
x=-2
0-2
1
2
-1
-3
-5
3
0,5
2) Đường thẳng
: 7 10
y x
cắt (C) tại 2 điểm A, B phân
biệt. Tính độ dài AB.
(1.0 điểm)
* Phương trình hoành độ giao điểm của (C) và (
):
2
7 10 2 7 10 2 , 2
2
xx x x x x
x
2 2
1 3
2 7 24 20 7 25 18 0 18
8
7
x y
x x x x x x y
* Vậy (
) cắt (C) tại 2 điểm phân biệt:
18
1;3 , ; 8
7
A B
* Khoảng cách giữa 2 điểm A,B là:
2
2 2 2
18 55 2
1 8 3
7 7
B A B A
AB x x y y
0,25
0,25
0,25
0,25
Câu 2 (2.0 điểm)
1) Tính giá trị biểu thức 2
3 log 3
1
3
2 3log 27
P
(1.0 điểm)
* 2
2
3
3 log 3
log 3
2 8
2
3
2
* 1
3
2
13
3
9
3log 27 3log 3
2
*
8 9 11
3 2 6
P
0,25
0,25
0,5
2) Tìm GTLN, GTNN của các hàm số
2
2 ln
y f x x x
trên đoạn 1
;
e
e
(1.0 điểm)
* Hàm số y=f(x) liên tục trên 1
;
e
e
*
1
' 4y x
x
* 2
1
( )
12
' 0 4 0 4 1 0 1
( )
2
x nhan
y x x
x
x loai
*
2
2
1 2 1 1 1
1, 2 1, ln
2 2 2
f f e e f
e e
* Ta thấy, 2
2
1 1 2
ln 1 2 1
2 2
e
e
* 1;
1 1 1
ln
2 2 2
e
e
Min y khi x
; 2
1;
2 1
e
e
Max y e khi x e
0,25
0,25
0,25
0,25
Câu 3 Cho khối chóp S.ABC biết SA vuông góc với mp(ABC), góc
giữa SC và mặt đáy bằng
0
30
;
ABC
vuông tại A có
3
AC a
,
฀
0
60
ACB
(2.0 điểm)
1) Tính thể tích khối chóp S.ABC (1.0 điểm)
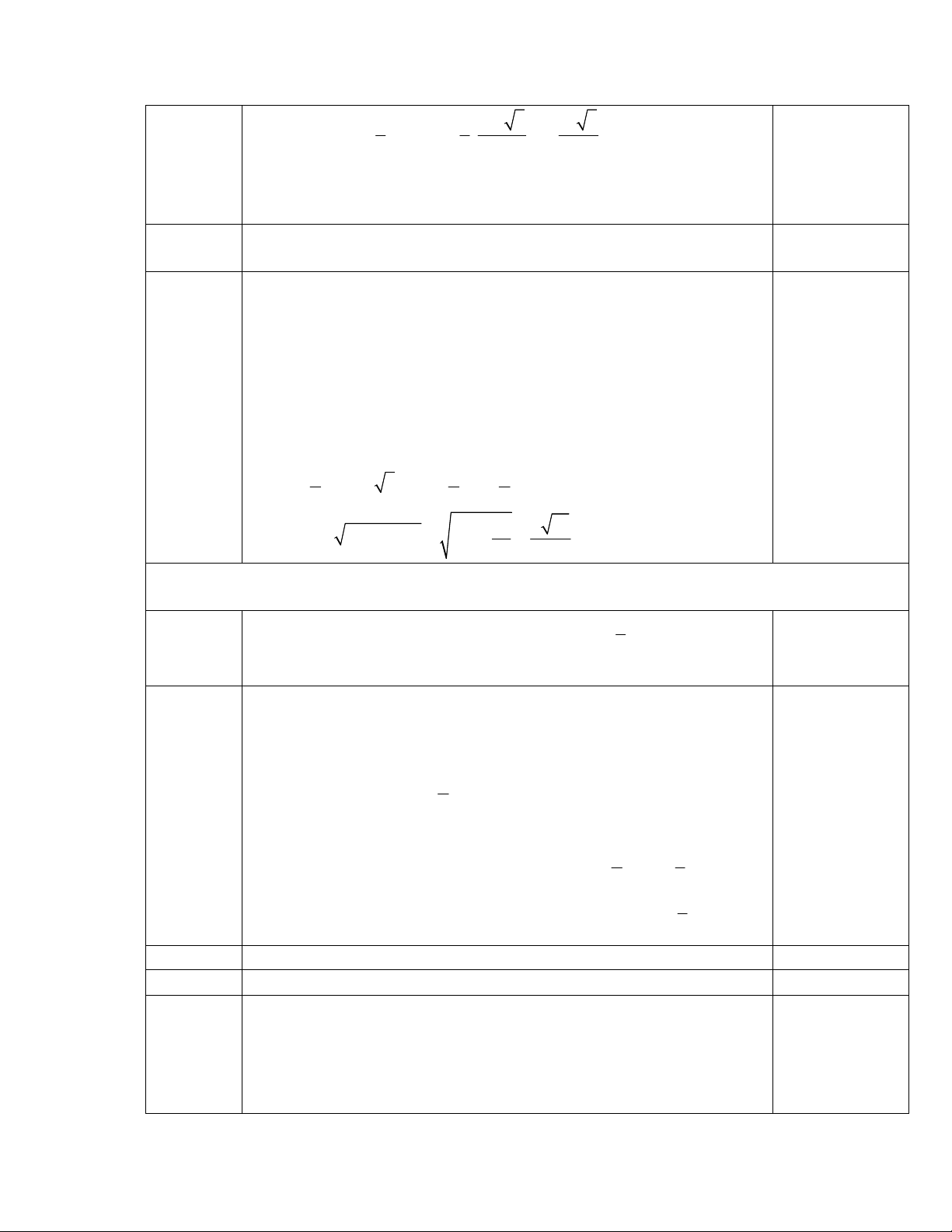
I
M
O
A B
C
S
* SA là đường cao hình chóp
* AC là hình chiếu của SC lên (ABC). Suy ra,
฀
฀
฀
0
,( ) , 30
SC ABC SC AC SCA
* Tam giác ABC vuông tại A. Ta có 0
.tan60 3
AB AC a
* Tam giác SAC vuông tại C. Ta có 0
.tan30
SA AC a
* Diện tích đáy: 2
1 3 3
.
2 2
a
S AB AC
0,25
* Thể tích: 2 3
1 1 3 3 3
. . .
3 3 2 2
ABC
a a
V S SA a 0,25
0,5
2) Xác định tâm và tính bán kính mặt cầu ngoại tiếp khối
chóp S.ABC
(1.0 điểm)
* Gọi O là trung điểm BC. Do
ABC vuông tại A nên O là
tâm đường tròn ngoại tiếp
ABC
* Dựng
đi qua O và song song SA. Ta có
là trục của
đường tròn ngoại tiếp
ABC
* Gọi M là trung điểm SA. Mặt phẳng trung trực của SA đi
qua M và cắt
tại I. Ta có: IA=IB=IC=IS
Suy ra, I là tâm mặt cầu ngoại tiếp hình chóp; bán kính
R=IS=IA
* 1 1
3;
2 2 2
a
AO BC a MA SA
* 2
2 2 2
13
3
4 2
a a
R AI AO OI a
0,5
0,25
0,25
II. PHẦN RIÊNG – PHẦN TỰ CHỌN (3.0 điểm)
Phần 1: Theo chương trình chuẩn
Câu 5.a Viết phương trình tiếp tuyến của
3 2
1
2 3 ( )
3
y f x x x x C
tại điểm có hoành độ
0
x
biết
0
" 0
f x
(1.0 điểm)
* Gọi
0 0 0
;
M x y
là tiếp điểm
* 2
'( ) 4 3; ''( ) 2 4
f x x x f x x
* 0 0
''( ) 0 2 4 0 2
f x x x
* Suy ra,
0
2
2
3
y f
, 0
'( ) '(2) 1
f x f
* Phương trình tiếp tuyến:
0 0 0
'
y f x x x y
2 8
1 2
3 3
x x
* Vậy phương trình tiếp tuyến cần tìm là:
8
3
y x
0,25
0,25
0,5
Câu 6.a (2.0 điểm)
1) 1
4 33.2 8 0
x x
(1.0 điểm)
* 1 2
4 33.2 8 0 4.2 33.2 8 0
x x x x
* Đặt
2 , ( 0)
x
t t
. Ta có phương trình:
0,25