
Đề số 10
KIỂM TRA 1 TIẾT CHƯƠNG III
Môn:HÌNH HỌC LỚP9
II.ĐỀ BÀI
Câu 1: (5 điểm)
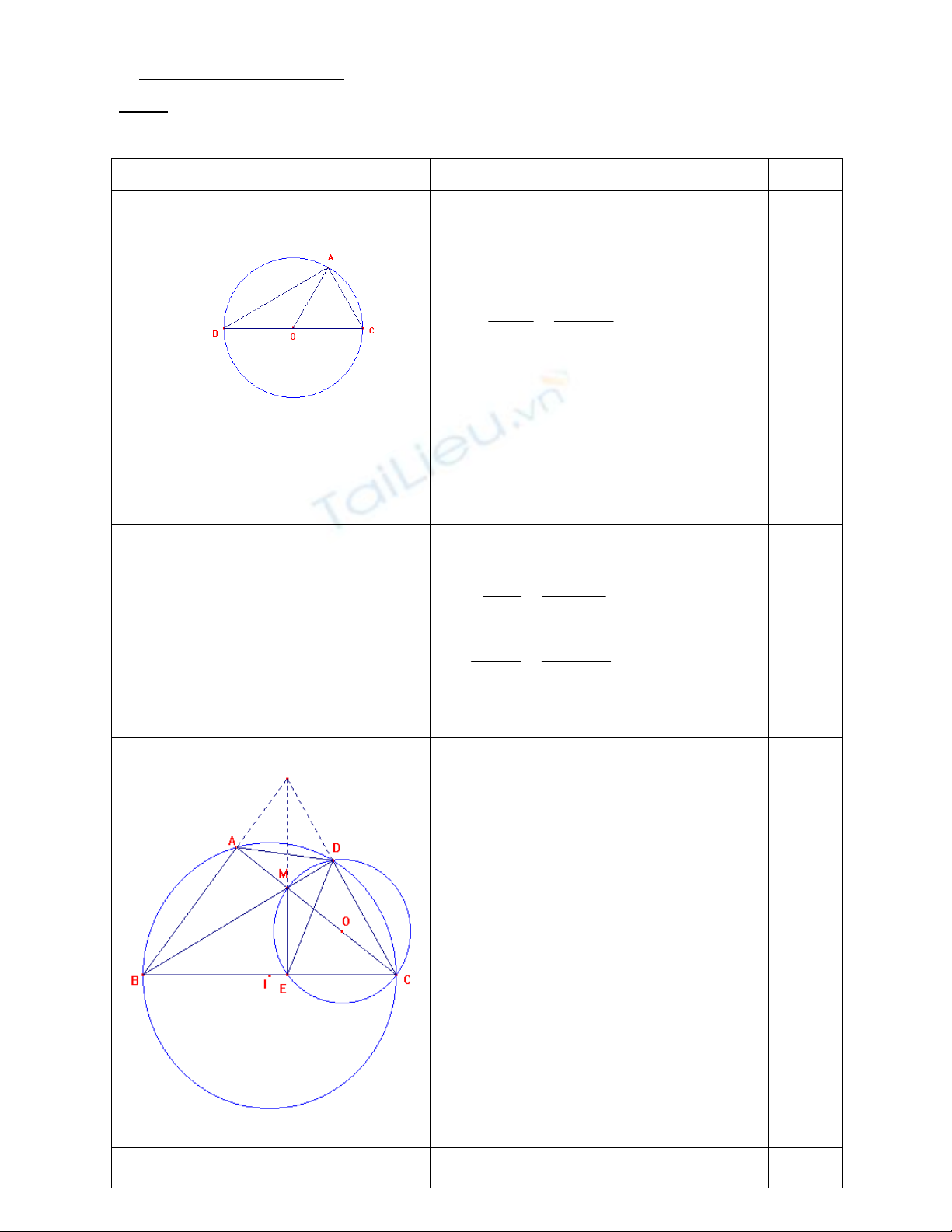
Cho tam giác ABC vuông tại A biết góc C bằng 600, AC = 6cm.
a) Tính chu vi đường tròn và diện tích hình tròn ngoại tiếp tam giác ABC.(3đ)
b) Tính độ dài cung tròn AB và diện tích hình quạt cung AB.(2đ)
Câu2: (5 điểm)
Cho ΔABC vuông tại A, trên cạnh AC lấy điểm M. Đường tròn đường kính MC cắt BC tại
E, BM cắt đường tròn tại D.
a) Chứng minh tứ giác ABCD nội tiếp. Xác định tâm I của đường tròn ngoại tiếp tứ giác.(2đ)
b) Chứng minh DB là phân giác góc ADE.(2đ)
c) Chứng minh AB, ME, CD đồng quy tại một điểm.(1đ)
II.ĐÁP ÁN & BIỂU ĐIỂM:
Câu2: (5 điểm)
Câu Nội dung trình bày Điểm
1a
(3 đ)
Ta có ΔABC vuông tại A
ΔABC nội
tiếp đường tròn đường kính BC.
AC = BC.cosC
0
AB 6
BC 12
cosC cos60
cm
R = 6cm.
C = 2R = 2.6=12 (cm)
S = R2 = .62 = 36 (cm2)
0,5đ
1đ
0,5đ
0,5đ
0,5đ
1b
(2đ) Ta có
0 0
C 60 s 0
đ
12
AB
Rn .6.120
l 4 (cm)
180 180
(1đ)
2 2
2
.R n .6 .120
S 12 (cm )
360 360
(1đ)
1đ
1đ
2a
Ta có
0
BAC 90
( gt)
0
MDC 90
( góc nội tiếp chắn
cung nửa đtr)
Hay
0
BDC 90
Suy ra
0
BDC BAC 90
Do đó tg ABCD nội tiếp đường
tròn đường kính BC. Tâm I là trung điểm
BC.
0,5đ
0.5 đ
0.5 đ
0.5 đ
2b Ta có
ADB ACB
(góc nội tiếp cùng

chắn cung AB của đường tròn I)
EDB ACB
(góc nội tiếp cùng chắn
cung ME của đường tròn O)
ADB BDE
hay DB là phân giác
ADE
0,5đ
0.5 đ
1đ
2c
Xét ΔBMC.
0
MEC 90
( góc nội tiếp chắn cung nửa
đường tròn) ME BC ME là
đường cao.
BA MC (
0
BAC 90
) BA là đường
cao.
CDBM (
0
BDC 90
) CD là đường
cao.
Vậy AB , CD, ME đồng quy tại một
điểm.
0,25đ
0,25 đ
0.25 đ


![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)




![Đề thi học kì 2 Vật lý lớp 11: Đề minh họa [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250709/linhnhil/135x160/711752026408.jpg)








