S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ
Đ NG THÁPỒ
Đ THI Đ XU TỀ Ề Ấ
Đ KI M TRA CH T L NG H C KÌ IỀ Ể Ấ ƯỢ Ọ
Năm h c: 2012- 2013ọ
Môn thi: Toán 11
Th i gian: 90 phút ( Không k th i gian phát đ )ờ ể ờ ề
Ngày thi: 10/ 01/ 2013
Đ n v ra đ : THPT L p Vò 3.ơ ị ề ấ
I. PH N CHUNGẦ: (8 đi m)ể
Câu 1 : (3 đi m ) ể
1).Tìm t p xác đ nh c a hàm s ậ ị ủ ố
tan(2 )
3
π
y x= −
2). Gi i các th ng trình l ng giác sau:ả ươ ượ
a).
2
2 cos 7 cos 3 0x x+ + =
b).
3 sin 2 cos 2 1x x− =
Câu 2 : (2 đi m)ể
1). Tìm h s c a s h ng ch a ệ ố ủ ố ạ ứ
12
x
trong khai tri n ể
12
2
1
xx
� �
−
� �
� �
2). M t h p có 7 bút bi xanh, 8 bút bi đ và 5 bút bi đen ch khác nhau v màu, l y ng uộ ộ ỏ ỉ ề ấ ẫ
nhiên t h p trên 3 bút bi. Tính xác su t đ trong 3 bút bi l y ra có đ 3 màu ?. ừ ộ ấ ể ấ ủ
Câu 3 : (1 đi m)ể
Trong m t ph ng Oxy, cho hai đi m A(1; 3) , B(3 ; 0) và đ ng th ng có ph ngặ ẳ ể ườ ẳ ươ
trình (d) 3x – 2y + 1 = 0 .Tìm nh (dả/) c a (d) qua phép t nh ti n theo véct ủ ị ế ơ
AB
uuur
.
Câu 4 : (2 đi m)ể
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, g i M, N l n l tọ ầ ượ
là trung đi m CD, AB và K là m t đi m trên SA sao cho 3SK = SA.ể ộ ể
1). Tìm giao tuy n c a hai m t ph ng (SAC) và (SBD) ;ế ủ ặ ẳ
2). Tìm thi t di n c a hình chóp S.ABCD c t b i m t ph ng (MNK).ế ệ ủ ắ ở ặ ẳ
II. PH N T CH NẦ Ự Ọ : (2 đi m)ể
H c sinh ch n ọ ọ 1 trong 2 ph n sau:ầ.
Ph n A: Theo ch ng trình chu nầ ươ ẩ :
Câu 5a : (1 đi m)ể
Cho c p s c ng ấ ố ộ có
2 5
19u u+ =
và
. Tìm s h ng đ u tiên, công sai c aố ạ ầ ủ
c p s c ng trên.ấ ố ộ
Câu 6a : (1 đi m)ể
T các ch s ừ ữ ố 1,2,3,4, 5 có th l p đ c bao nhiêu s ch n có 3 ch s khác nhau. ể ậ ượ ố ẵ ữ ố
Ph n B: Theo ch ng trình nâng caoầ ươ :
Câu 5b : (1 đi m)ể
Tìm giá tr l n nh t, giá tr nh nh t hàm s ị ớ ấ ị ỏ ấ ố
1
sin cos 2
yx x
=+ +
Câu 6b : (1 đi m)ể
T các ch s 1,2,3,4ừ ữ ố ,5 có th l p đ c bao nhiêu s có 3 ch s khác nhau vàể ậ ượ ố ữ ố
chia h t cho 3. H T.ế Ế
S GIÁO D C VÀ ĐÀO T OỞ Ụ Ạ
Đ NG THÁPỒ
Đ THI Đ XU TỀ Ề Ấ
Đ KI M TRA CH T L NG H C KÌ IỀ Ể Ấ ƯỢ Ọ
Năm h c: 2012- 2013ọ
Môn thi: Toán 11
Th i gian: 90 phút ( Không k th i gian phát đ )ờ ể ờ ề
Ngày thi: 10/ 01/ 2013
Đ n v ra đ : THPT L p Vò 3.ơ ị ề ấ
H NG D N CH M Đ THI Đ XU TƯỚ Ẫ Ấ Ề Ề Ấ
CÂU N I DUNG YÊU C UỘ Ầ ĐI MỂ
Câu 1
1) Hàm s xác đ nh khi ố ị
23 2
x k
π π π
− +
5
12 2
x k
π π
+
V y TXD: ậ
5
\ ;
12 2
D R k k Z
π π
� �
= +
� �
�
0,5
0,5
2)
1
cos 2
cos 3( )
x
x PTVN
= −
= −
22 ;
3
x k k Z
ππ
= +
0,5
0,5
3) Đ a PT v ư ề
1
sin(2 )
6 2
x
π
− =
Tìm
6( )
2
x k
k Z
x k
ππ
ππ
= +
= +
0,5
0,5
Câu 2
1)Vi t đ c s h ng t ng quát: ế ượ ố ạ ổ
( )
( ) ( )
12 24 3
2
1 12 12
11
k
kk k
k k
k
T C x C x
x
−−
+
� �
= − = −
� �
� �
Tìm k=4
V y h s là 495ậ ệ ố
0,5
0,25
0,25
2) L y 3 bút ng u nhiên có ấ ẫ
3
20
( ) 1140n CΩ = =
A: Là bi n c l y 3 bút có đ 3 màu: ế ố ấ ủ
( ) 7 8 5 208n A x x= =
Xác su t : ấ
14
( ) 57
P A =
0,25
0,5
0,25
Câu 3: Tìm đ c véc t ượ ơ
( )
2; 3AB = −
uuur
Vi t đ c công th c: ế ượ ứ
' 2
' 3
x x
y y
= +
= −
Tìm đ c PT d’: ượ
3 2 11 0x y− − =
0,25
0,25
0,5
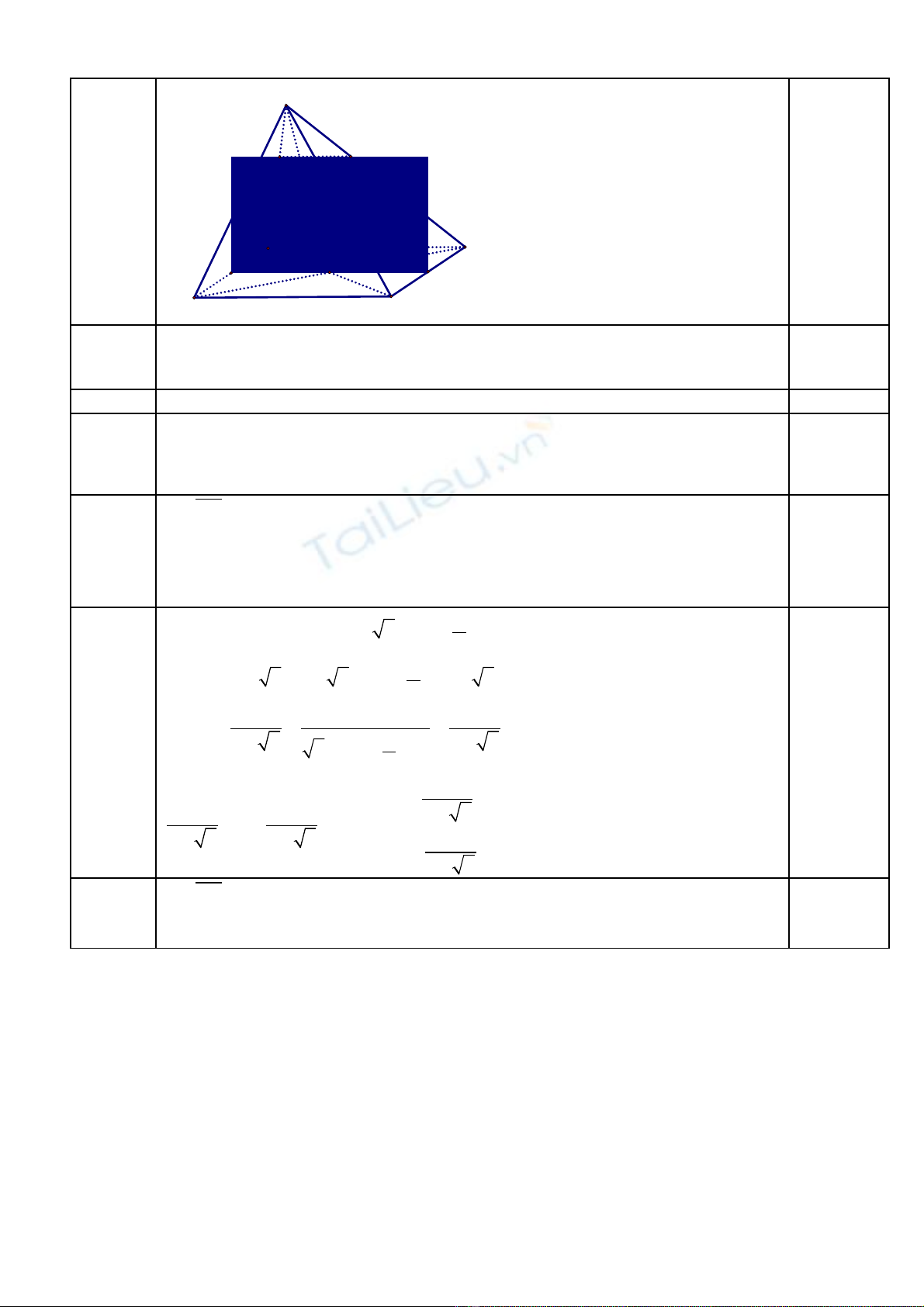
Câu 4: a) HS Tìm đ c hai đi m chungượ ể
là S và O
Ch đ c giao tuy n là SOỉ ượ ế
0,5
0,5
b) Tìm đ c giao tuy n KQ c a mp (MNK) v i m t (SAD)ượ ế ủ ớ ặ
Ch ra đ c thi t di n là hình thang MNKQỉ ượ ế ệ 0,5
0,5
PH N T CH NẦ Ự Ọ
Câu 5a
HS đ a v đ c h : ư ề ượ ệ
1
1
2 5 19
5
u d
u d
+ =
+ =
Gi i h tìm uả ệ 1 = 2; d= 3
0,5
0,5
Câu 6a
n abc=
c ch n nên có 2 cáchẵ
a khác c nên có 4 cách
b khác c,a nên có 3 cách
V y có 24 s c n tìmậ ố ầ
1
Câu 5b Bi n đ i ế ổ
sin cos 2 2 sin( ) 2
4
x x x
π
+ + = + +
Tìm đ c ượ
2 2 2 sin( ) 2 2 2
4
x
π
− + + + +
Đ a v ư ề
1 1 1
2 2 2 2
2 sin( ) 2
4
x
π
− +
+ +
1 1
2 2 2 2
y
− +
Tìm
1;
2 2
1
2 2
Miny
Maxy
=−
=+
0,25
0,25
0,25
0,25
Caau 6b
n abc=
Ta tìm các t p {a, b, c} mà t ng a+b+c chia h t cho 3ậ ổ ế
Có 4 t p {1,2,3} ;{1,3,5}; {2,3,4}; {3,4,5}. V i m i t p ta s p đ c 6 s có baậ ớ ỗ ậ ắ ượ ố
ch s khác nhau và chia h t cho 3. V y có 24 s ữ ố ế ậ ố
1
Q
N
M
O
D
A
B
C
S
K