SỞ GD VÀ ĐT NGHỆ AN
TRƯỜNG THPT NGUYỄN XUÂN ÔN
ĐỀ THI HỌC SINH GIỎI CẤP TRƯỜNG
NĂM HỌC: 2017-2018
MÔN TOÁN: KHỐI 10
Thời gian: 150 phút (không kể thời gian phát đề)
Câu I:(2điểm)Tìm tập xác định của hàm số:
2
1 2017
2018 4
yxxx

Câu II: (3điểm) Cho phương trình:
22
( 5 6)( 9 20) 2 1 0 (1)x x x x m
Tìm
m
để phương trình
(1)
có nghiệm
thỏa mãn:
27 9 0xx
Câu III:(5điểm)
1.(2điểm)Giải phương trình:
3 1 2 2 7 2x x x
2.(3điểm)Giải hệ phương trình:
33
3
21
2
x x y
xy x


Câu IV:(2điểm) Cho hình vuông
ABCD
. Điểm
,IJ
xác định bởi:
11
,
32
BI BC CJ CD
Đường thẳng
AI
cắt
BJ
tại
K
.Chứng minh:
AK
vuông góc với
CK
Câu V:(2 điểm)
Câu VI(3điểm)
Cho tam giác
ABC
với
(5;6), (1;2)AB
đường phân giác trong của góc A song song với
trục tung, góc C bằng
0
60
. Tìm tọa độ đỉnh C.
Câu VII.(3điểm)
Xét hình chữ nhật ABCD và điểm M di động trên BC. Phân giác góc DAM cắt BC tại
N. Hãy xác định vị trí của M để
MN
AN
đạt giá trị nhỏ nhất.
…....................................…….Hết……..................................….
(Học sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.)
B
A
M
N
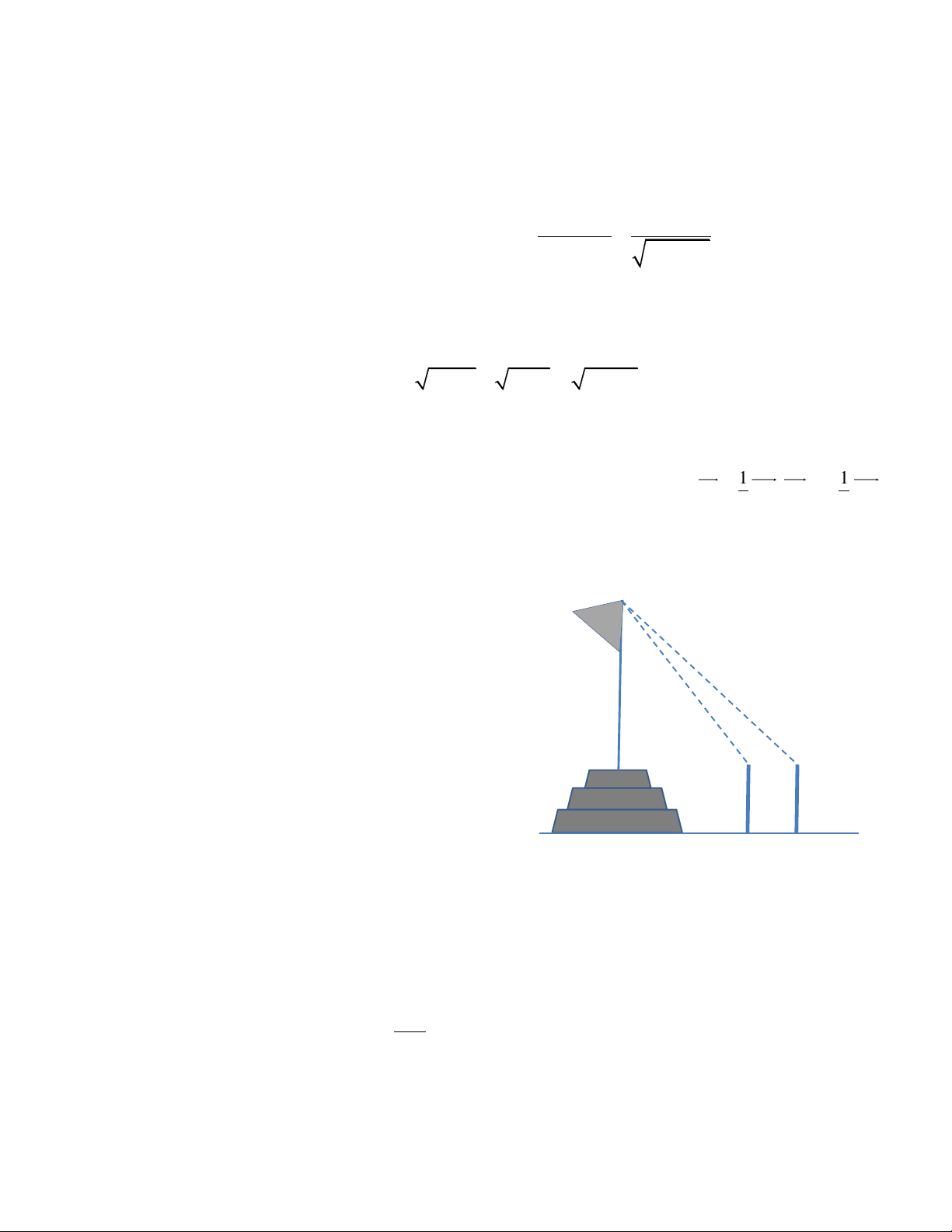
Để đo chiều cao từ mặt đất đến đỉnh cột cờ
của một kỳ đài trước Ngọ Môn (Đại Nội-Huế),
người ta cắm hai cọc AM và BN cao 1,5 mét
so với mặt đất. Hai cọc này song song và cách
nhau 10 mét và thẳng hàng so với tim cột cờ
(Hình vẽ minh họa). Đặt giác kế tại đỉnh A và
B để nhắm đến đỉnh cột cờ, người ta được các
góc lần lượt là
0'
51 40
và
0'
45 39
so với đường
song song với mặt đất. Hãy tính chiều cao của
cột cờ (làm tròn 0,01 mét).
Đáp án và hướng dẫn chấm
Câu
Lời giải
Điểm
Câu I
(2đ)
Điều kiện:
2
2018 0
40
x
xx


1,0
2018
0
4
x
x
x
0,5
D=
;0 (4;2018) (2018; ) 
0,5
Câu II
(3điểm)
22
( 5 6)( 9 20) 2 1 0 (1)x x x x m
22
(7 10)( 7 12) 2 1 0 (2)xx x x m
1,0
Đặt:
279t x x
suy ra
0t
0,5
Khi đó (2) trở thành: (t+1)(t + 3) -2m -1 = 0, (với t ≤ 0) (3)
0,5
PT (1) có nghiệm x thỏa mãn đề bài khi và chỉ khi pt (3) có nghiệm t thỏa mãn: t ≤ 0
Xét: t2 + 4t +2 = 2m ( Với t ≤ 0) (*)
Xét hàm số: f(t) = t2 + 4t+2 ( với t ≤ 0)
t
-∞ - 2 0
+∞
f(t)
+∞
2
-2
Suy ra (*) có nghiệm khi: 2m ≥ -2
m ≥ -1
Kết luận: pt(1) có nghiệm x thỏa mãn đề bài khi: m ≥ -1
0,5
0,5
Câu III
(5điểm)
1.(2điểm)Giải phương trình:
3 1 2 2 7 2x x x
ĐK: x ≥ 2,
0,25
khi đó phương trình đã cho trở thành:
3 1 2 2 72x x x
0,5
3 1 4 3 1 4 2 7 2 ( 2)(2 x 7) 2x x x x x
0,25
2 3 1 ( 2)(2 7)x x x
0,25
2
2 9 18 0xx
0,25
6
3
2
x
x

0,25
Đối chiếu với điều kiện, suy ra phương trình đã cho có nghiêm x = 6
0,25
2. (3điểm)Giải hệ phương trình:
33
()
3
21
2I
x x y
xy x


Đặt
1
xt
Khi đó hệ (I) trở thành:
3
3
12
12
yt
ty


0,5
22
3
( )( 2) 0
12
t y t ty y
ty

0,5
3
0
12
ty
ty


0,5
32 1 0
ty
yy
0,5
1
15
2
15
2
ty
y
y
y

0,5
Suy ra hệ có nghiệm (x,y) là: (-1;-1);(
51
2
;
51
2
); (
5 1 2
;)
215

0,5
CâuIV
(2điểm)
Đặt độ dài cạnh hình vuông bằng a,
,AB a AD b
, khi đó:
a b a
,
.0ab
0,25
Giả sử
BK xBJ
, ta có:
11
, (1 )
32
AI a b AK AB BK x a xb
0,5
Vì
,AI AK
cùng phương nên ta có:
12
13
25
x x x
0,25
Khi đó ta có:
1,
3
AI a b
13
55
CK a b
0,5
Xét:
22
1 1 3 1 1
. ( )( ) 0
3 5 5 5 5
AI CK a b a b a a
0,25
Suy ra
AI
vuông góc với
CK
, hay AK vuông với CK
0,25
Câu VI
(2điểm)
A
B
C
D
K
I
J
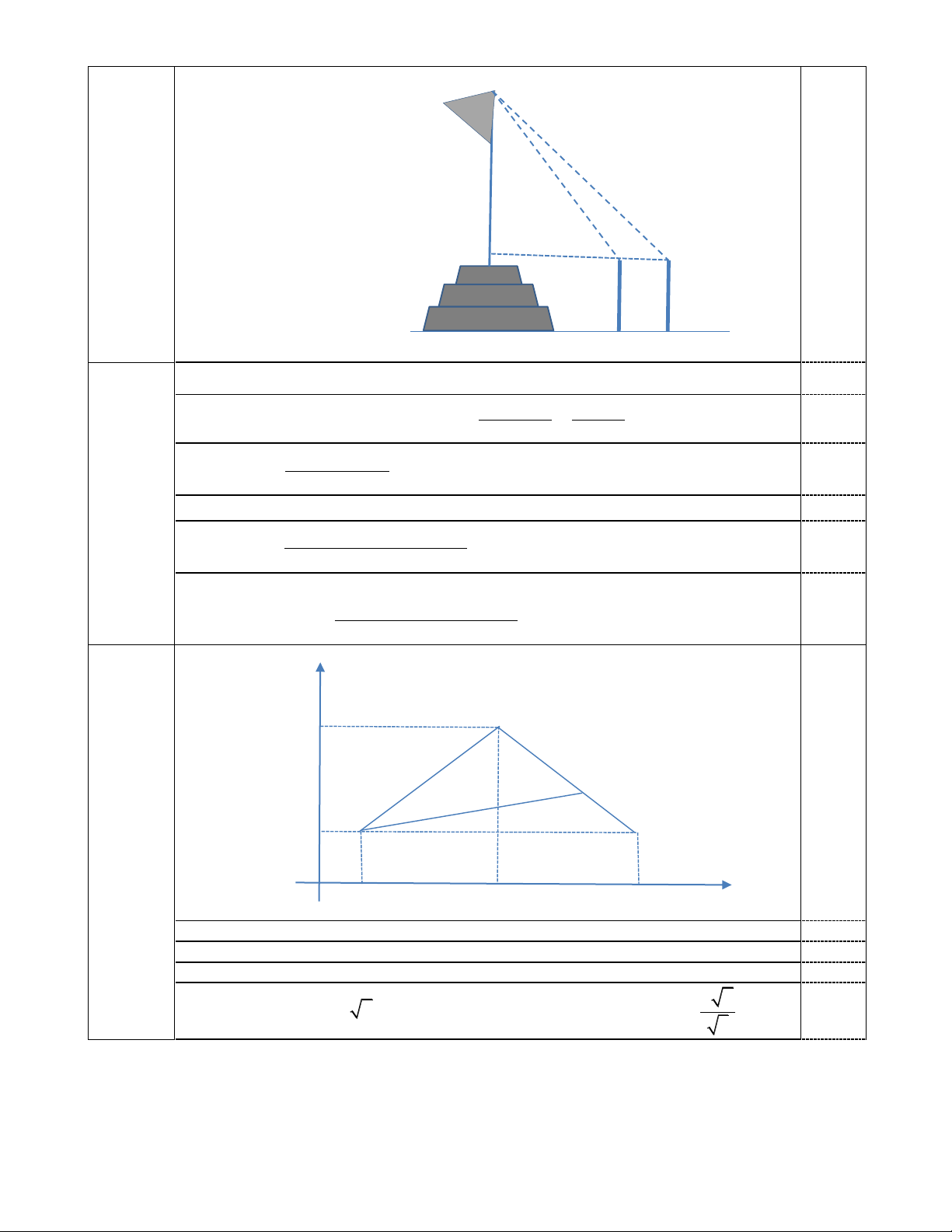
Ta có:
0 ' 0 '
128 20 , 6 1CAB ACB
0,25
Áp dụng định lý hàm số sin trong
0 ' 0
:sin 45 39 sin 6 1'
AC AB
ABC
0,5
Suy ra:
0
0
.sin 45 39'
sin 6 1'
AB
AC
0,25
Xét trong tam giác vuông ACD:
0
.sin51 40'CD AC
0,25
Suy ra:
00
0
.sin 45 39'.sin51 40'
sin 6 1'
AB
CD
0,25
Suy ra chiều cao cột cờ là:
00
0
.sin 45 39'.sin51 40'
1,5 1,5 55,01( )
sin 6 1'
AB
h CD m
0,5
Câu VII
(3điểm)
Đường phân giác trong của góc A song song với trục Oy nên có phương là x = 5(d)
0,25
Gọi B’ là điểm đối xứng của B qua (d), suy ra B’(9;2) và
ABB’ vuông cân tại A
0,25
Suy ra C thuộc cạnh AB’
0,25
Xét
ABC
, có
00
4 2, 90 , 60AB A C
suy ra
042
.cot 60 3
AC AB
0,5
B
A
M
N
C
D
B
A
B’
5
1
2
6
9
x
y
O
I
C
Gọi C(x;y), khi đó ta có:
42
3
AC AB
AC
(I)
0,5
( 4; 4); ( 5; 6)AB AC x y
0,25
Theo (I) ta có hệ:
22
11
32
( 5) ( 6) 3
xy
xy

0,5
Giải Hệ (2) có nghiệm:
4
53
4
63
x
y


hoặc
4
53
4
63
x
y


0,5
Câu VIII
(3điểm)
Đặt AB = a; AD = b; AM = m> 0, AN = n > m;
AMN
= .
0,25
Theo giả thiết ta có:AN là phân giác góc
MAD
MAD ANB
(cùng bằng
NAD
)
Vậy ANM cân tại M MN = AM = m.
0,5
Theo định lý cosin cho ANM có:
)cos1(m2cos.m.m2mmn 2222
0,5
)cos1(2mn
0,25
Theo bài ra ta có:
)cos1(2
m
)cos1(2m
m
n
MN
AN
0,5
Ta có:>900(vì M di động trên đoạn BC)cos0
2)cos1(2
MN
AN
0,5
MN
AN
đạt giá trị nhỏ nhất khi
2
MN
AN
,
xảy ra cos = 0 =900 M B.
0,5
Chú ý: - Chấm phải bám biểm điểm đã cho, không thay đổi biểu điểm
- Học sinh làm cách khác đúng vẫn cho điểm tối đa.
D
A
B
C
M
N