Kỳ thi Olimpic THPT thị xã Bỉm Sơn lần thứ nhất - năm 2009
Đề thi đề nghị của trường THPT Lê Hồng Phong (Bỉm Sơn)
SỞ GIÁO DỤC VÀ ĐÀO TẠO THANH HOÁ
TRƯỜNG THPT LÊ HỒNG PHONG
KỲ THI OLIMPIC THPT THỊ XÃ BỈM SƠN LẦN THỨ NHẤT NĂM 2009
ĐỀ ĐỀ NGHỊ MÔN: TOÁN; LỚP 11
Đường cắt phách
Câu hỏi 1:(3 điểm) Giải phương trình:
4sin52x- 4sin2x+ 2(sin6x+ sin4x)+ 1= 0
Đáp án NỘI DUNG ĐIỂM
Biến đổi được phương trình
Û
4sin25x+ 4sin5xcosx+ cos2x= 3sin2x
Û
(2sin5x- cosx)2=3sin2x
Û
[
[
ê
ê
ë
é
-=
+=
)2(sin35sin2
)1(sin35sin2
xosxcx
xosxcx
Giải các phương trình (1) và (2) được nghiệm
2
24
p
p
k
x+= ,
3
36
5
p
p
k
x+= ,
3
36
p
p
l
x+= ,
2
24
5
p
p
l
x+=
(
)
Zlk Î,
0.5
0.5
0.5
1.5
Số phách
Số phách
Kỳ thi Olimpic THPT thị xã Bỉm Sơn lần thứ nhất - năm 2009
Đề thi đề nghị của trường THPT Lê Hồng Phong (Bỉm Sơn)
SỞ GIÁO DỤC VÀ ĐÀO TẠO THANH HOÁ
TRƯỜNG THPT LÊ HỒNG PHONG
KỲ THI OLIMPIC THPT THỊ XÃ BỈM SƠN LẦN THỨ NHẤT NĂM 2009
ĐỀ ĐỀ NGHỊ MÔN: TOÁN; LỚP 11
Đường cắt phách
Câu hỏi 2: (3 điểm) Giải phương trình với nghiệm nguyên:
(x2 + y )(x + y2 ) = (x + y)3
Đáp án NỘI DUNG ĐIỂM
Biến đổi được phương trình
Û
xy(1+xy - 3x - 3y ) = 0
ê
ê
ê
ë
é
=+++
=
=
Û
)3(0133
)2(0
)1(0
yxxy
y
x
Khi x= 0 Zay
Î
=
Khi y= 0 Zbx
Î
=
(3)
Û
x(y+3)= 3y-1
Û
3
10
3+
-= y
x
ê
ê
ê
ê
ê
ê
ê
ê
ê
ê
ê
ë
é
-=+
=+
-=+
=+
-=+
=+
-=+
=+
Þ
103
103
53
53
23
23
13
13
y
y
y
y
y
y
y
y
Từ đó dẫn đến (x; y)=(-7;-2),(13; -4),(-2;-1),(8; -5),(1; 2),(5; -8),(2; 7),(4; -13)
0.5
0.5
1.0
1.0
Số phách
Số phách
Kỳ thi Olimpic THPT thị xã Bỉm Sơn lần thứ nhất - năm 2009
Đề thi đề nghị của trường THPT Lê Hồng Phong (Bỉm Sơn)
SỞ GIÁO DỤC VÀ ĐÀO TẠO THANH HOÁ
TRƯỜNG THPT LÊ HỒNG PHONG
KỲ THI OLIMPIC THPT THỊ XÃ BỈM SƠN LẦN THỨ NHẤT NĂM 2009
ĐỀ ĐỀ NGHỊ MÔN: TOÁN; LỚP 11
Đường cắt phách
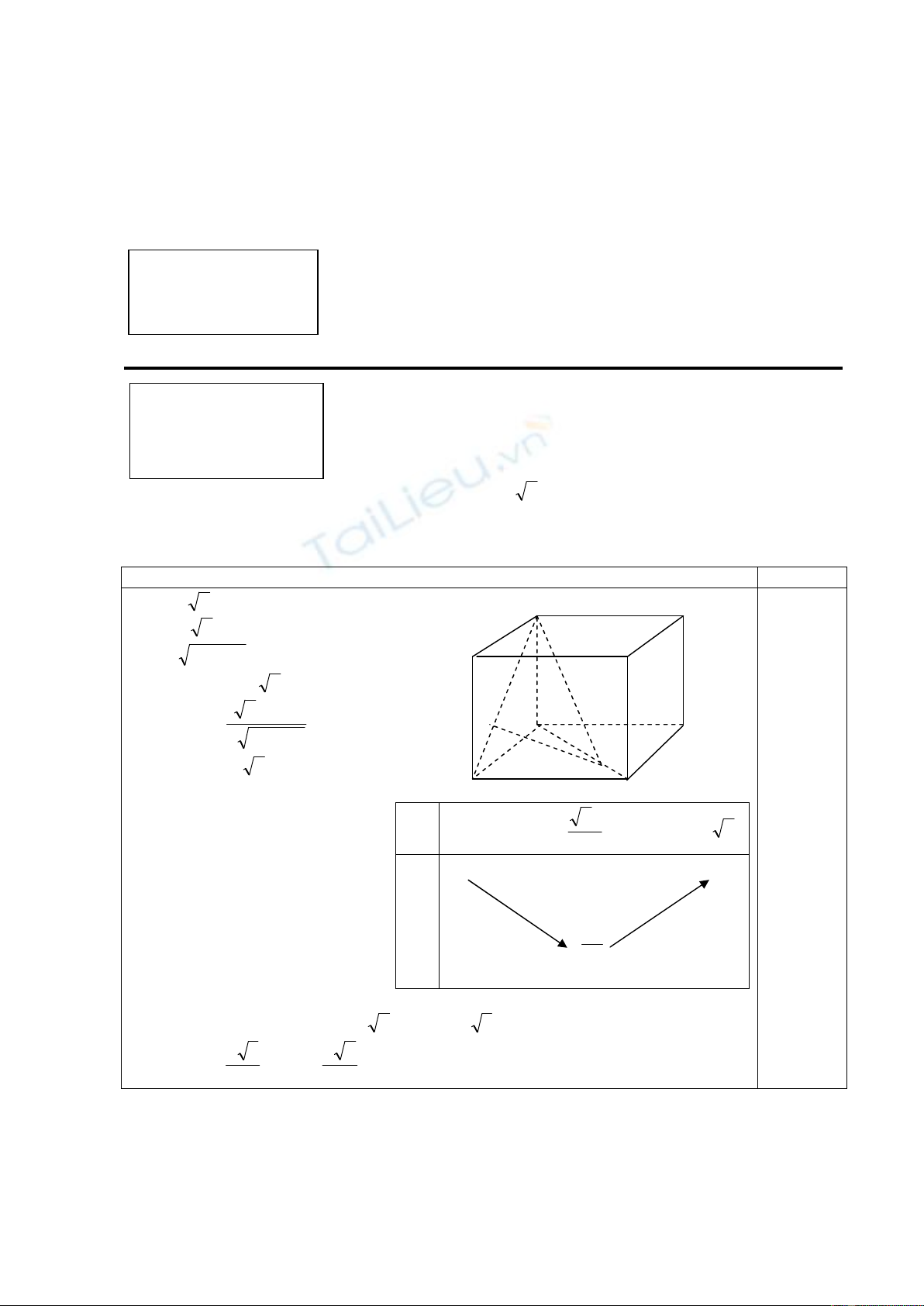
Câu hỏi 3:(4 điểm) Cho hình lập phương ABCDA’B’C’D’ cạnh a.
Gọi M, N là hai điểm di động trên hai cạnh AD’ và BD sao cho
AM= DN= x ( 20 ax ££ ). Tìm x để MN có độ dài nhỏ nhất, lớn
nhất.
Đáp án: NỘI DUNG ĐIỂM
2' aAD = , D' C'
xaMD -= 2'
22
'xaND += A' B'
axxaAN 2
222 -+=
22
2
2
'cos xa
xax
NMD +
+
= M D C
)(223 222 xfaaxxMN =+-= A N B
L ập bảng biến thi ên cho f(x) x 0
3
2a 2a
f(x)
a2 3a2
3
2
a
T ừ đó MN2 lớn nhất khi x= 2a và MN= 3a và MN nhỏ nhất khi MN2nhỏ nhất
Khi đó MN=
3
3a khi x
3
2a
=
0.5
0.5
0.5
0.5
0.5
0.5
0.5
0.5
SỞ GIÁO DỤC VÀ ĐÀO TẠO THANH HOÁ
TRƯỜNG THPT BỈM SƠN
KỲ THI OLIMPIC THPT THỊ XÃ BỈM SƠN LẦN THỨ NHẤT NĂM 2009
Số phách
Số phách
Kỳ thi Olimpic THPT thị xã Bỉm Sơn lần thứ nhất - năm 2009
Đề thi đề nghị của trường THPT Lê Hồng Phong (Bỉm Sơn)
ĐỀ ĐỀ NGHỊ MÔN: TOÁN; LỚP 11
Câu hỏi 4:(3 điểm)
Cho các số thực dương a, b, c thoả mãn: abc=1
Tìm giá trị nhỏ nhất của P=
b
c
a
c
ab
a
b
c
b
ca
c
a
b
a
bc
222222
+
+
+
+
+
Đường cắt phách
NỘI DUNG ĐIỂM
cbca
ba
babc
ac
acab
cb
cbcac
ab
babcb
ca
acaba
bc
P+
+
+
+
+
=
+
+
+
+
+
=222222
)()()(
Đánh giá được: bc
acab
ac
ab
cb ³
+
+
+
4
22
ca
babc
ba
bc
ac ³
+
+
+
4
22
ab
cbca
cb
ca
ba ³
+
+
+
4
22
( )
2
3
2
3
2
32³³
+
+
³abc
cabcab
P
Dấu = xảy ra khi a=b=c
0.5
1.0
1.0
0.5
SỞ GIÁO DỤC VÀ ĐÀO TẠO THANH HOÁ
TRƯỜNG THPT BỈM SƠN
Số phách
Số phách
Kỳ thi Olimpic THPT thị xã Bỉm Sơn lần thứ nhất - năm 2009
Đề thi đề nghị của trường THPT Lê Hồng Phong (Bỉm Sơn)
KỲ THI OLIMPIC THPT THỊ XÃ BỈM SƠN LẦN THỨ NHẤT NĂM 2009
ĐỀ ĐỀ NGHỊ MÔN: TOÁN; LỚP 11
Câu hỏi 5:(4 điểm)
Cho dãy số (un) xác định bởi u1=1và un+1=6un-1
a) Hãy tính u2009.
b) Tính tổng 2009 số hạng đầu tiên của dãy (un).
Đường cắt phách
NỘI DUNG ĐIỂM
a) Phân tích được: ÷
ø
ö
ç
è
æ-=-
+5
1
6
5
1
1nn uu
Đặt
5
1
-= nn uv dẫn đến vn+1=6vn từ đó (vn) là một cấp số nhân với v1=
5
4 và công bội
q= 6
5
1
6
5
4
6
5
411 +=Þ= -- n
n
n
nuv
5
1
6
5
42008
2009 +=Þ u
(
)
5
2009
6...661
5
420082
2009 +++++=S
5
100456.4
5
2009
5
16
5
420082009 +
=+
-
=
1.0
0.5
1.0
0.5
0.5
0.5
SỞ GIÁO DỤC VÀ ĐÀO TẠO THANH HOÁ
Số phách
Số phách