PHÒNG GDĐT NGHĨA HƯNG
TRƯỜNG THCS NGHĨA LỢI
ĐỀ CHÍNH THỨC
ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA HỌC KÌ I
NĂM HỌC 2022 – 2023
Môn : Toán - Lớp 9 THCS
(Thời gian làm bài: 90 phút)
Đề khảo sát gồm 1 trang
I. Phần trắc nghiệm: (2 điểm)
Khoanh tròn vào chữ cái đứng trước câu trả lời mà em cho là đúng.
Câu 1: Căn bậc hai số học của 4 là
A. -16 . B. 16 . C. 2 . D. 2 .
Câu 2: Điều kiện xác định của biểu thức là
A. . B. . C. . D. .
Câu 3: Rút gọn biểu thức với a >1 ta được
A. . B. . C. . D. .
Câu 4: Giá trị biểu thức bằng
A. . B. . C. . D. .
Câu 5: Giá trị của x sao cho là
A. -13. B. -1. C. 5. D. 14.
Câu 6: Cho tam giac ABC vuông tại A, đường cao AH. Biết BH = 3cm, HC = 4cm. Khi đó độ dài AH bằng
A. cm . B. cm. C. cm. D. 12cm.
Câu 7: Giá trị biểu thức bằng
A. B. C. D. 1.
Câu 8: Cho tam giác MNP vuông ở M có MN = a, MP = a (với a>0). Số đo góc MPN bằng
A. 300. B. 450. C. 600. D. 350.
II. Phần tự luận: (8 điểm)
Câu 9: Rút gọn các biểu thức sau:
a, b,
Câu 10: Cho biểu thức với .
a, Rút gọn P .
b, Chứng minh , với mọi x thoả mãn và .
Câu 11: Giải phương trình: .
Câu 12: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 6 cm, ABC = 600.
a, Tính độ dài các đoạn thẳng AH, BH, HC.
b, Trên tia AB, AH lần lượt lấy các điểm D, E sao cho AB = BD (DA), HE = 2 HA. Gọi K là hình chiếu
của A trên DC. Chứng minh: HC . BC + DK . DC = DC2.
c, Tính tanHCE và chứng minh DEC = 900.
Câu 13: Cho và thoả mãn x + y =1.
Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức .
……………………….HẾT……………………….
1
III. HƯỚNG DẪN CHẤM
PHÒNG GDĐT NGHĨA HƯNG
TRƯỜNG THCS NGHĨA LỢI
ĐỀ KIỂM TRA CHẤT LƯỢNG GIỮA HỌC KÌ I
NĂM HỌC 2022 – 2023
HƯỚNG DẪN CHẤM MÔN TOÁN- LỚP 9
I, Trắc nghiệm khách quan ( 2điểm) Mỗi câu đúng được 0,25 điểm
Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8
C D B C A B D A
II, Tự luận : ( 8 điểm)
Câu Lời giải Điểm
Câu 9a
(0,5đ)
0,25
0,25
Câu 9b
(1đ)
0,5
0,25
0,25
Câu 10a
(1đ)
với .
Vậy với .
0,25
0,25
0,25
0,25
Câu 10b
(0,5đ)
Theo câu a, ta có với .
()
(vì )
luôn đúng với mọi
Vậy , với mọi x thoả mãn và .
0,25
0,25
Câu11
(1đ)
(ĐK:
Vậy phương trình có 1 nghiệm .
0,25
2
0,25
0,25
0,25
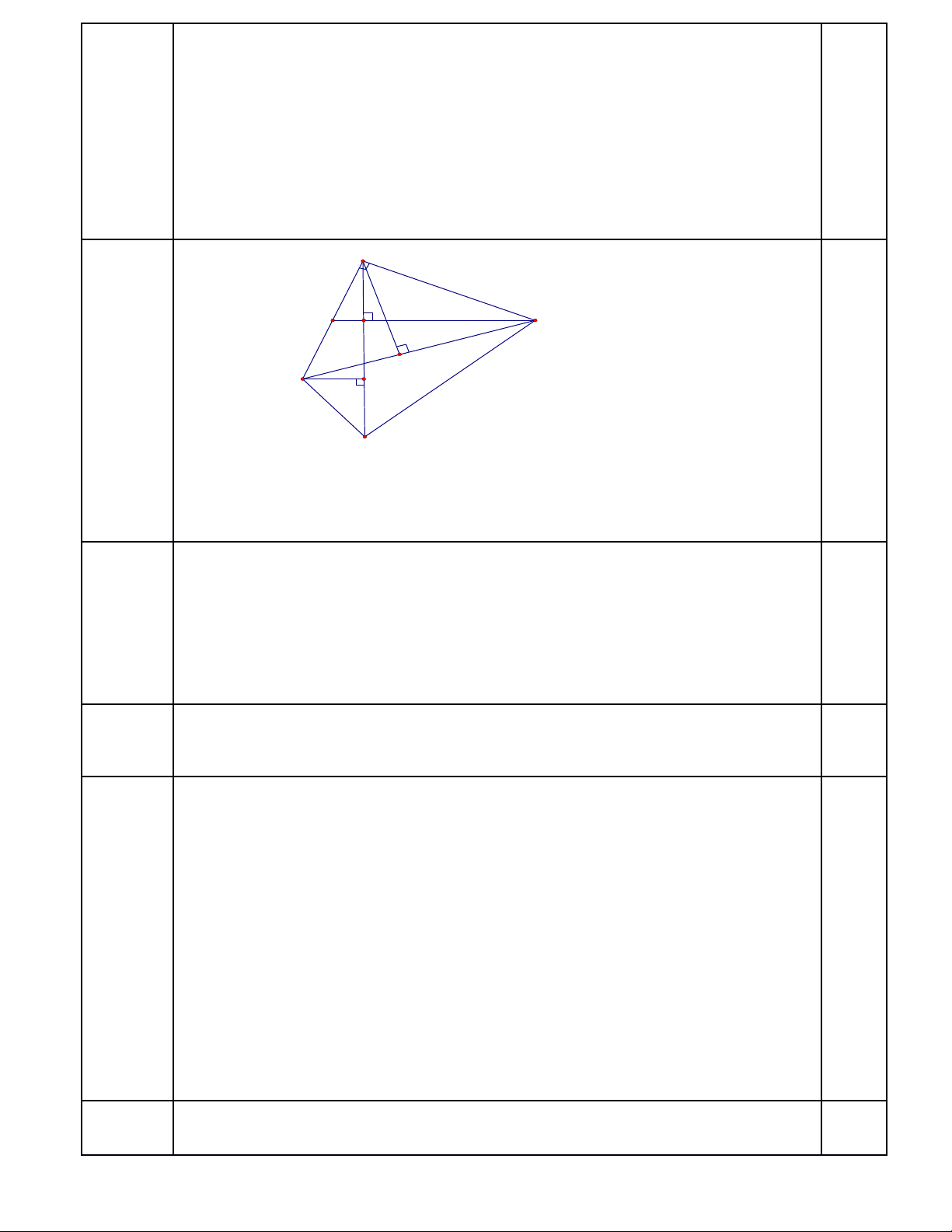
Câu 12
H
A
D
C
E
B
I
K
Câu 12a,
(1đ)
+ ABH vuông tại H có
+ ABC vuông tại A có AH BC
0,25
0,25
0,5
Câu 12b,
(1đ)
+ABC vuông tại A, đường cao AH có: AC2 = HC . BC (1)
+ADC vuông tại A, đường cao AK có: AD2 = DK.DC (2)
và AC2 + AD2 = DC2 (3)
Từ (1), (2), (3) suy ra HC . BC + DK . DC = DC2.
0,25
0,25
0,25
0,25
Câu 12c,
(1đ)
+ Có HE = 2HA= (cm)
+HEC vuông tại H có (1)
+Kẻ DI AE tai E
lại có BC AE (gt)
suy ra DI // BC
+ADI có BH//DI , AB = BD suy ra (hqĐLTa lét)
+ DIE vuông tại I có (2)
Từ (1) và (2) suy ra =>
Lại có HCE + HEC = 900 ( EHC = 900)
=> DEI + HEC = 900
=> DEC = 900
0,25
0,25
0,25
0,25
Câu 13
(1đ)
.
Ta có P > 0
3
Vì (vì P > 0)
Dấu “=” xảy ra (TMĐK)
áp dụng bất đẳng thức côsi ta có
Dấu “=” xảy ra (TMĐK)
Vậy GTLN của P là , GTNN của P là .
0,5
0,5
……………………….HẾT……………………….
4
5