SỞ GIÁO DỤC-ĐÀO TẠO ĐĂKLĂK
TRƯỜNG THPT BUÔN MA THUỘT
THI HỌC KỲ I, NĂM HỌC 2008-2009
MÔN: TOÁN LỚP 10, CHƯƠNG TRÌNH NÂNG CAO
Thời gian làm bài: 90 phút (không kể giao đề)
Bài 1 ( 3 điểm):
1. Giải phương trình:
3 7 1 2
x x
2. Giải hệ phương trình:
2 2
4
2
x xy y
x y xy
Bài 2 ( 3 điểm):
1. Tìm phương trình Parabol ( P) biết ( P) cắt trục tung tại điểm có tung độ bằng 2, cắt trục hoành
tại hai điểm có hoành độ bằng 1và 2.
2. Định m để phương trình: 2 2
2( 2) 16 0
x m x m
có hai nghiệm dương phân biệt .
Bài 3 ( 3 điểm):
1. Cho tam giác ABC có cạnh
2 3, 2
a b
và góc
0
ˆ
30
C. Tính c, S, ha và R.
2. Cho tam giác ABC biết A(1;-3), B(3;-5) và C(2;-2).
a) Tình chu vi tam giác ABC.
b) Gọi E là giao điểm của BC với đường phân giác ngoài của góc A, tìm tọa độ điểm E.
Bài 4 ( 1 điểm): Cho ba số dương a,b,c. Chứng minh rằng:
2 2 2
4
3
a b c
a b
b c a
CHÚ Ý: Các kết quả không dùng phép tính gần đúng
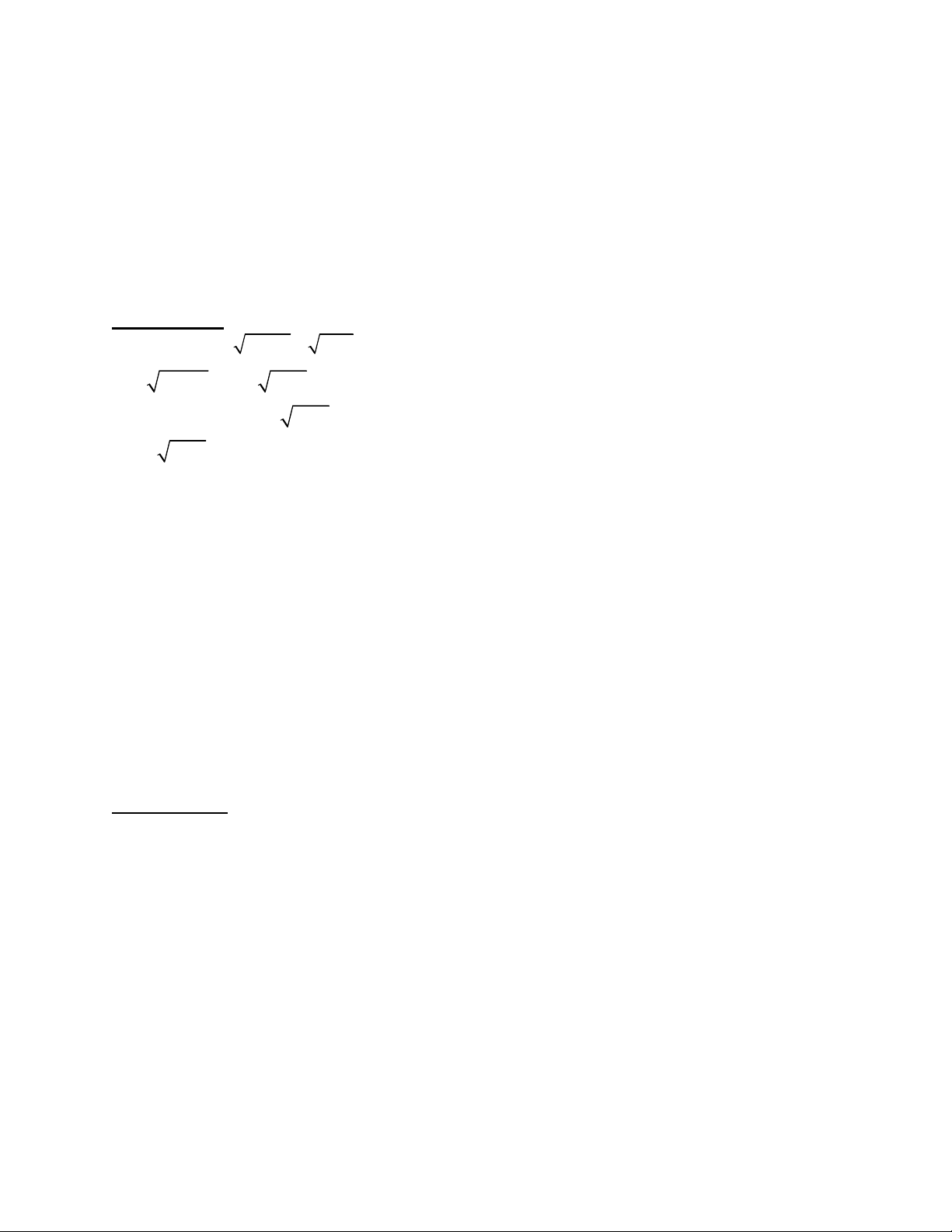
SỞ GIÁO DỤC-ĐÀO TẠO ĐĂKLĂK
TRƯỜNG THPT BUÔN MA THUỘT
THI HỌC KỲ I, NĂM HỌC 2008-2009
ĐÁP ÁN MÔN: TOÁN LỚP 10, CHƯƠNG TRÌNH NÂNG CAO
Thời gian làm bài: 90 phút (không kể giao đề)
Bài 1( 3 điểm)
1) ( 1,5 điểm)
3 7 1 2
x x
(1). Đkiện:
1
x
ta có (1) ( 0.25)
(0.5)
(0.25)
( thoả mãn đk) (0.5)
2) ( 1,5 điểm)
2 2
4
2
x xy y
x y xy
2
4
2
S P
S P
với
S x y
P xy
(0.25)
2
6 0
2
S S
P S
(0.5)
Kết quả: * S = -3, P = 5 ( loại vì S2 < 4P) (0.25)
* S = 2, P = 0 . Ta có x, y là nghiệm pt: x2 -2x = 0
0 2
x x
(0.25)
Vậy nghiệm của hệ: ( 0;2) và (2;0) (0.25)
Bài 2 ( 3 điểm)
1) ( 1 điểm) Gọi ( P ): y = ax2 + bx + c.
Vì A( 0;2), B(1;0), C(2;0) thuộc ( P) nên ta có: (0.25)
2 1
0 3
4 2 0 2
c a
a b c b
a b c c
(0.5)
Vậy ptrình ( P): y = x2 – 3x +2 (0.25)
2) ( 2 điểm) Ptrình: 2 2
2( 2) 16 0
x m x m
. Ta có:
2
2
3 7 2 1
3 7 5 4 1
2 1 1
4( 1) 2 1
2 3 0 1 3
x x
x x x
x x
x x x
x x x x
'
1 2
2
0 20 4 0
0 0 2 0
0
16 0
5
2 4 5
4 4
m
x x S m
Pm
m
m m
m m
(1.0
)
(1.0)
Bài 3 ( 3 điểm)
1) ( 1.0 điểm)
2 3, 2
a b
,
0
ˆ
30
C
c2 = a2 + b2 – 2ab.cosC = 12 + 4 -2.
2 3.2
3
2
= 4. Suy ra c = 2 ( 0.25)
1 1 1
sin .2 3.2. 3
2 2 2
S ab C (0.25)
1 2 2 3
1
22 3
a a
S
S ah h a
(0.25)
2
2
2sin 2.0,5
c
RC
(0.25)
2) ( 2.0 điểm) a)
AB =
2 2
; BC =
10
; AC =
2
(0.5)
Chu vi 2p =
3 2
+
10
(0.5)
b) Ta có: 2 2 2 2
2
EB AB
EB EC
EC AC
(0.5)
3 2(2 ) 1
5 2( 2 ) 1
E E E
E E E
x x x
y y y
(0.5)
Kết quả: E (1;1)
Bài 4 ( 1 điểm) Ta có:
2
2
2
2
4 4
4
4
a
b a
b
b
c b
c
c
a c
a
( Mỗi bất đẳng thức 0.25 x 3 = 0.75 )
Cộng các bất đẳng thức trên theo vế ta có:
2 2 2
4
3
a b c
a b
b c a
( 0.25)
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
TRƯỜNG THPT CHU VĂN AN
ĐỀ THI HỌC KỲ I NĂM HỌC 2012- 2013
Môn: Toán lớp 10 Nâng cao
Dành cho tất cả các lớp
Buổi thi: … ngày …/…/2012
Thời gian làm bài:
120 phút
, không kể thời gian giao đề
Đề thi gồm 01 trang
----------------------
Câu 1. (1 điểm) Cho hàm số
2
3
4
( )
9
x
f x
x x
.
a. Tìm tập xác định của hàm số.
b. Xét tính chẵn, lẻ của hàm số.
Câu 2. (2 điểm) Giải các phương trình và hệ phương trình:
a. 2
2 4 2
x x x
. b.
1 2
2
5 3
1
2
x x y
x y x
.
Câu 3. (2,5 điểm) Cho hàm số 2
(2 5) 2( 1) 3
y m x m x
có đồ thị
m
C
.
a. Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi
2
m
.
b. Chứng minh rằng khi
5
2
m
thì
m
C
luôn cắt đường thẳng
( ) : 3 3
d y x
tại
hai điểm có tọa độ không đổi.
Câu 4. (4 điểm)
1. Cho tam giác
ABC
, lấy các điểm
,
M N
sao cho
2 0,3 2 0
MA MB NA NC

.
a. Biểu thị ,
AM AN

theo
,
AB AC
.
b. Chứng minh
, ,
M N G
thẳng hàng, trong đó
G
là trọng tâm tam giác
ABC
.
c. Giả sử
, 5 , 2 3
AB a AC a MN a
với
0
a
, tính số đo góc
฀
BAC
của tam
giác
ABC
.
2. Trong mặt phẳng tọa độ cho
(1;1), ( 1;3), (0;1)
A B H
.
a. Chứng minh
, ,
A B H
không thẳng hàng.
b. Tìm tọa độ điểm
C
sao cho
H
là trực tâm tam giác
ABC
.
Câu 5. (0,5 điểm)
Giải hệ phương trình
2
3
4
x xy y
x y
x xz z
x z
y yz z
y z
------------------ HẾT ------------------