TRƯỜNG THCS PHƯỚC BỬU ĐỀ KIỂM TRA CUỐI HỌC KỲ I
TỔ TOÁN - TIN NĂM HỌC 2024 – 2025
MÔN: TOÁN 8 (90 phút)
(Không kể thời gian giao đề)
Bài 1 (1,5 điểm). Phân tích các đa thức sau thành nhân tử:
a) 3x – 6 ; b)
2
x 64−
c)
( )
x x 3 + 2x 6−−
Bài 2 (2,0 điểm). Thực hiện các phép tính sau:
a)
x2
+
x +3 x +3
b)
2
2xx
x y x 2
−
−
Bài 3 (1,5 điểm).
a) Rút gọn biểu thức:
( )
3 1 3x + 2 2
A x 2 ; x 2
x 2 x + 2 x 4 x 2
2:

= + −


−
− − −
b) Tìm giá trị nguyên của x để phân thức
x + 4x + 4
Px4
=−
2
2
nhận giá trị nguyên.
Bài 4 (1,5 điểm).
a) Điểm kiểm tra giữa học kì I 3 môn Văn, Toán, Anh văn của bạn Hoa được ghi lại như
sau:
STT
Môn
Xếp loại
1
Toán
Khá
2
Văn
Trung bình
3
Anh văn
Giỏi
Hãy phân loại dữ liệu trong bảng thống kê trên dựa trên hai tiêu chí định tính và định lượng.
b) Thời gian chạy 100 m (tính theo giây) của 24 học sinh được ghi lại trong bảng số liệu
ban đầu sau:
14
15
16
16
14
15
14
16
16
15
15
14
15
15
14
16
15
15
16
16
15
15
16
14
Hãy chuyển đổi dữ liệu từ bảng số liệu ban đầu trên sang dạng bảng thống kê.
Bài 5 (3,5 điểm). Cho tam giác ABC vuông tại A. M là trung điểm của cạnh BC. Qua M vẽ MH
vuông góc với AB tại H và MK vuông góc với AC tại K (
H AB, K AC
).
a) (1,0 đ). Cho AB = 3 cm, AC = 4 cm. Tính độ dài cạnh BC.
b) (1,0 đ). Chứng minh tứ giác AHMK là hình chữ nhật.
c) (0, 5 đ). Tính độ dài HK.
d) (0,5 đ). Gọi N là điểm đối xứng của M qua H. Chứng minh góc ANM = góc BMN
----- Hết -----
ĐỀ CHÍNH THỨC
( ĐỀ CHẴN)
TRƯỜNG THCS PHƯỚC BỬU KIỂM TRA CUỐI HỌC KỲ I, TOÁN 8
TỔ TOÁN – TIN NĂM HỌC 2024 - 2025
HƯỚNG DẪN CHẤM ĐỀ CHẴN
Bài
Hướng dẫn
Điểm
Bài 1 (1,5 điểm)
Phân tích các đa thức sau thành nhân tử:
a) 3x – 6 ; b)
2
x 64−
c)
( )
x x 3 + 2x 6−−
a) 3x – 6 = 3(x – 2)
b)
( )( )
2
x 64= x 8 x 8− − +
c)
( ) ( ) ( )( )
x x 3 + 2x 6= x x 3 + 2(x 3)= x 3 x 2− − − − − +
0,5
0,5
0,5
Bài 2 (2,0 điểm)
Thực hiện các phép tính sau:
a)
x2
+
x +3 x +3
b)
2
2
xx
x y x 2
−
−
a)
x 2 x +2
+
x +3 x +3 x +3
=
b)
22
2 2) 1
2)
x x (x x
x y x 2 x y (x xy
− −
==
−−
1,0
1,0
Bài 3 (1,5 điểm)
a) Rút gọn biểu thức
( )
3 1 3x + 2 2
A x 2 ; x 2
x 2 x + 2 x 4 x 2
2:

= + − −

− − −

b) Tìm giá trị nguyên của x để phân thức
x + 4x + 4
Px4
=−
2
2
nhận
giá trị nguyên.
( )
( )( ) ( )
( )( ) ( )( )
( ) ( )
( )( )
3 1 3x + 2 2
a) A x 2 x + 2 x 4 x 2
3 x + 2 1 x 2 3x + 2 x 2
x + 2 x 2 x + 2 x 2 x + 2 x 2 2
3 x + 2 x 2 3x + 2) x2
x + 2 x 2 2
1 x 2
x 2 2
1 x 2)
(x 2) 2
2:
1(
1
2
(

= + −

− − −


−−
= + −

− − −



+ − − −
=

−


−
=
−
−
==
−
x + 4x + 4 (x 2) x 2 x 2 4 4
b) P (x 2)(x 2) x 2 x 2 x 2
x4
2
2
21= = = = +
+ + − +
=− + − − −
−
P nguyên
4
x2−
nguyên
x 2) x 24(− −
((4)
x2 1; 2; 4 −
HS giải từng trường hợp và kết hợp điều kiện suy ra
x 0;1;3;4;6
0,25
0,25
0,25
0,25
0,25
0,25
Bài 4 (1,5 điểm)
a) Điểm kiểm tra giữa học kì I 3 môn Văn, Toán, Anh văn của bạn
Hoa được ghi lại như sau:
STT
Môn
Điểm
Xếp loại
1
Toán
7
Khá
2
Văn
6
Trung bình
3
Anh văn
9
Giỏi
Hãy phân loại dữ liệu trong bảng thống kê trên dựa trên hai
tiêu chí định tính và định lượng.
b)Thời gian chạy 100 m (tính theo giây) của 24 học sinh được ghi
lại trong bảng số liệu ban đầu sau:
14
15
16
16
14
15
14
16
16
15
15
14
15
15
14
16
15
15
16
16
15
15
16
14
Hãy chuyển đổi dữ liệu từ bảng số liệu ban đầu trên sang dạng
bảng thống kê.
a) HS phân loại đúng (1 đ). Sai một dữ liệu trừ (0,25 đ)
b)
Thời gian
chạy (giây)
14
15
16
Số học sinh
6
10
8
1,0
0,5
Bài 5 (3,5 điểm)
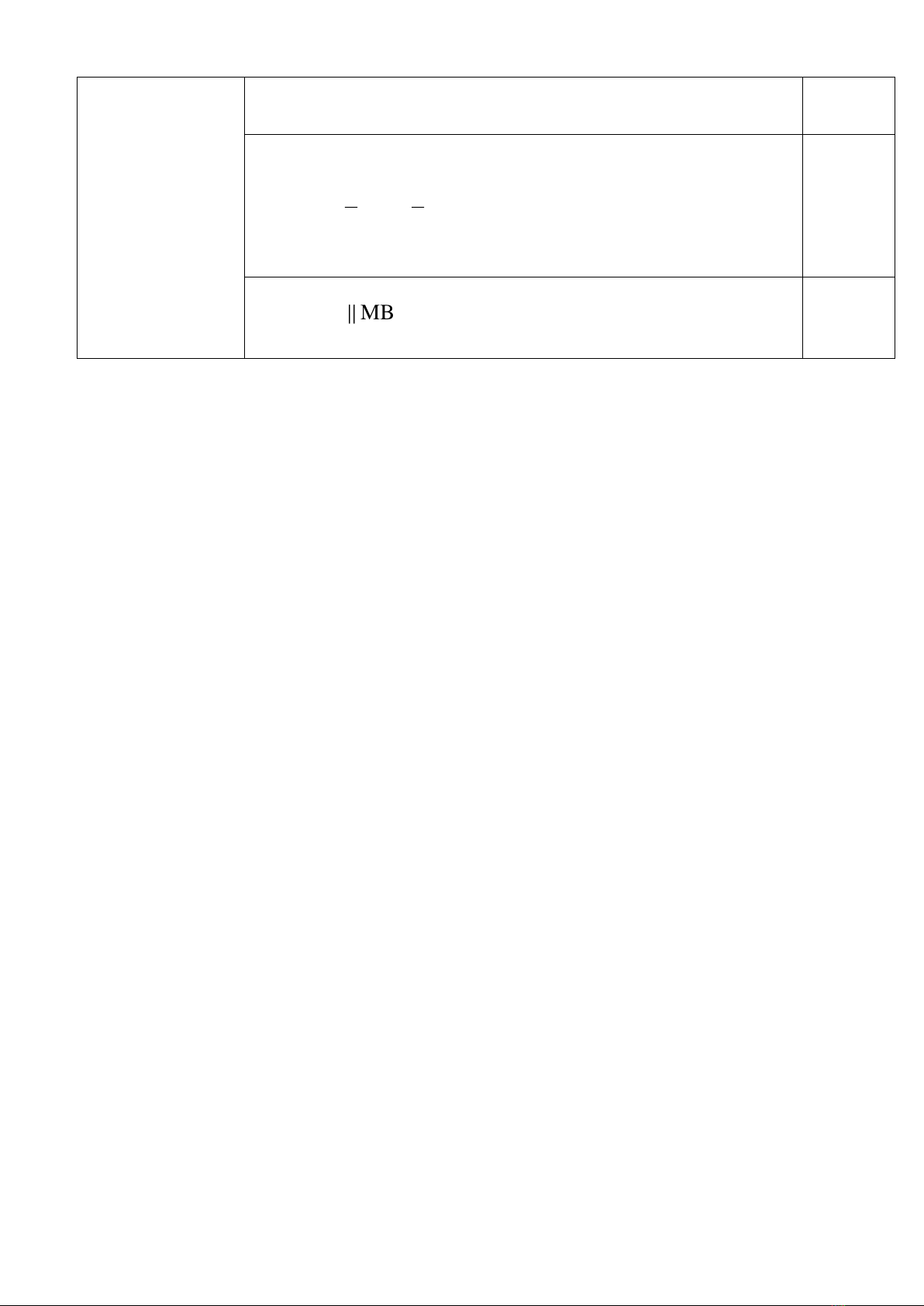
Cho tam giác ABC vuông tại A. M là trung điểm của cạnh BC. Qua
M vẽ MH vuông góc với AB tại H và MK vuông góc với AC tại K
(
H AB, K AC
).
a)(1,0 điểm). Cho AB = 3 cm, AC = 4 cm.Tính độ dài cạnh BC.
b) (0,75 điểm). Chứng minh tứ giác AHMK là hình chữ nhật.
c) (0,75 điểm). Tính độ dài HK.
d) (0,75 điểm) Gọi N là điểm đối xứng của M qua H. Chứng minh
ANM = BMN
0,5
a) Áp dụng định lí pythagore cho tam giác ABC vuông tại A, ta
có:
2 2 2 2 2
BC AB AC 3 4 25
BC 25 5
= + = + =
=
=
0, 5
0, 5
b) Xét tứ giác AHMK có :
0
HAK = 90
( tam giác ABC vuông tại A)
(AHM = 90 MH AB)
0⊥
0,25
0,25
B
A
C
K
M
H
N
Chú ý: Học sinh làm cách khác, đúng cho điểm tối đa.
(
AKM = 90 MK AC)
0⊥
Suy ra tứ giác AHMK là hình chữ nhật ( tứ giác có 3 góc vuông)
0,25
0,25
c) Ta có: Tứ giác AHMK là hình chữ nhật (cmt)
Suy ra HK = AM (tính chất hai đường chéo).
Mà
11
AM = BC = 5 = 2,5
22
cm (đường trung tuyến ứng với cạnh
huyền trong tam giác vuông)
Nên HK = AM = 2,5 cm
0,25
0,25
d) HS chứng minh được tứ giác ANBM là hình bình hành
Suy ra
AN MB
( tính chất 2 cạnh đối của hình bình hành)
Suy ra
ANM = BMN
(so le trong)
0,25
0,25