ĐẠI HỌC QUỐC GIA TP HCM
TRƯỜNG PHỔ THÔNG NĂNG KHIẾU
--------------------------------------
KIỂM TRA HỌC KỲ II NĂM HỌC 2018 – 2019
MÔN THI : TOÁN
KHỐI 11 – CHƯƠNG TRÌNH NÂNG CAO
Ngày thi : Thứ Hai 02/5/2019
Thời gian làm bài: 90 phút, không kể thời gian giao đề
----------------------------------------------
Bài 1. (1,5đ) Tính các giới hạn sau:
a)
2
lim 9 12 3
xx x x
 
. b)
2
2
3
3 7 4( 3)
lim .
( 3)
x
x x x
x
Bài 2. (1đ) Tính đạo hàm của các hàm số sau:
a)
2
(1 2 ) 1 2 .y x x x
22
) cos (1 2 ).b y x
Bài 3. (1đ) Chứng minh phương trình
2 3 3 2
(m 2 3)( 3 4) 0m x x m x
có ít nhất một nghiệm
với mọi số thực m.
Bài 4. (1đ) Tìm m để hàm số
liên tục trên
[ 2;2]
.
Bài 5. (1,5đ) Cho hàm số
21
() 1
x
y f x x

(C).
a) Viết phương trình tiếp tuyến tại giao điểm của đồ thị hàm số (C) và đường thẳng
21yx
.
b) Viết phương trình tiếp tuyến của đồ thị hàm số (C ) biết tiếp tuyến song song với đường thẳng
3 1 0xy
.
Bài 6. (4đ) Hình chóp S.ABCD có O là tâm của hình thoi ABCD, AB = a, , SA ⊥
(𝐴𝐵𝐶𝐷),
3SA a
. Dựng OK ⊥ SC ( K thuộc SC).
a) Chứng minh
BD
(SAC)
. Tính khoảng cách giữa hai đường thẳng BD và SC.
b) Tính góc tạo bởi đường thẳng SA và mặt phẳng (SBD).
c) Tính khoảng cách từ C đến mặt phẳng (SBD).
d) Tính góc tạo bởi hai mặt phẳng (KBC) và (OBC).
HẾT
Đáp án và cho điểm
Bài 1
Tìm giới hạn
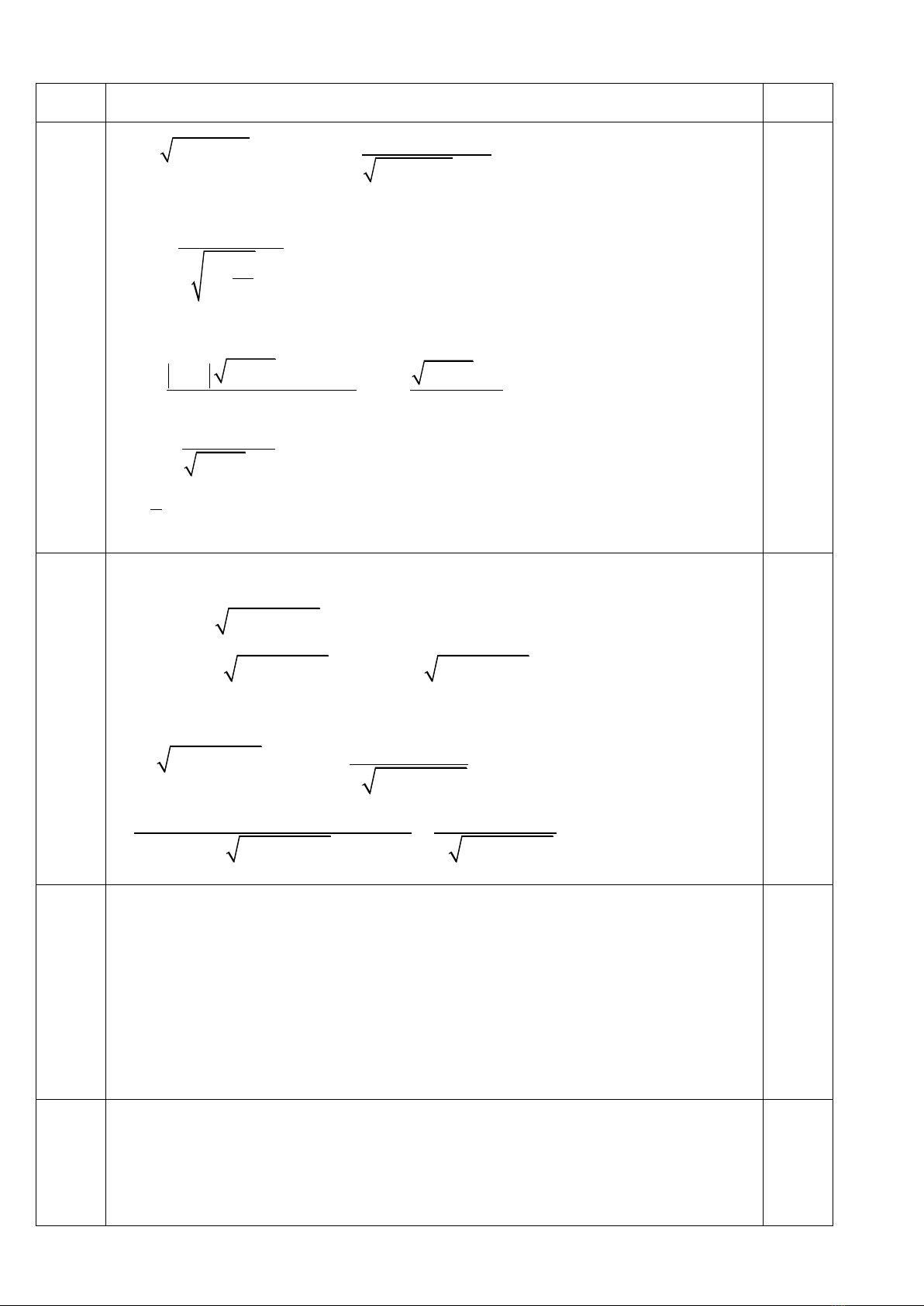
a)
b)
2
2
2
12
lim 9 12 3 lim
9 12 3
12
lim
12
93
2
xx
x
x
x x x
x x x
x








22
233
2
3
3 7 4( 3) 47
limlim 3)(3)(
3
lim
47
3
4
xx
x
x x x x
xx
x
x

Bài 2
Tính đạo hàm hàm số
2
22
2
2
22
22
(1 2 ) 1 2 .
y' (1 2 )' 1 2 (1 2 ) 1 2
14
2 1 2 (1 2 )
2 1 2
16 10 34(1 2 ) (1 2 )(1 4 )
2 1 2 2 1 2
y x x x
x x x x x x
x
x x x
xx
x xx x x x
x x x x


'
22
22
222
22
2
) cos (1 2 )
2cos(1 2 ).sin(1 2 ). (1 2 )'
= 8 cos(1 2 ).sin(1 2 ).
4 .sin(2 4 ).
b y x
x x x
x x x
xx





y'
2
cos(1
2x
).
cos(1
2x
)
'
Bài 3
Chứng minh rằng phương trình
2 3 3 2
(m 2 3)( 3 4) 0m x x m x
(1) có ít nhất
một nghiệm với mọi số thực m.
Đặt
2 3 3 2
( ) (m 2 3)( 3 4)f x m x x m x
.
Hàm số
()fx
xác định và liên tục trên R
Hàm số
()fx
liên tục trên [-1;1]
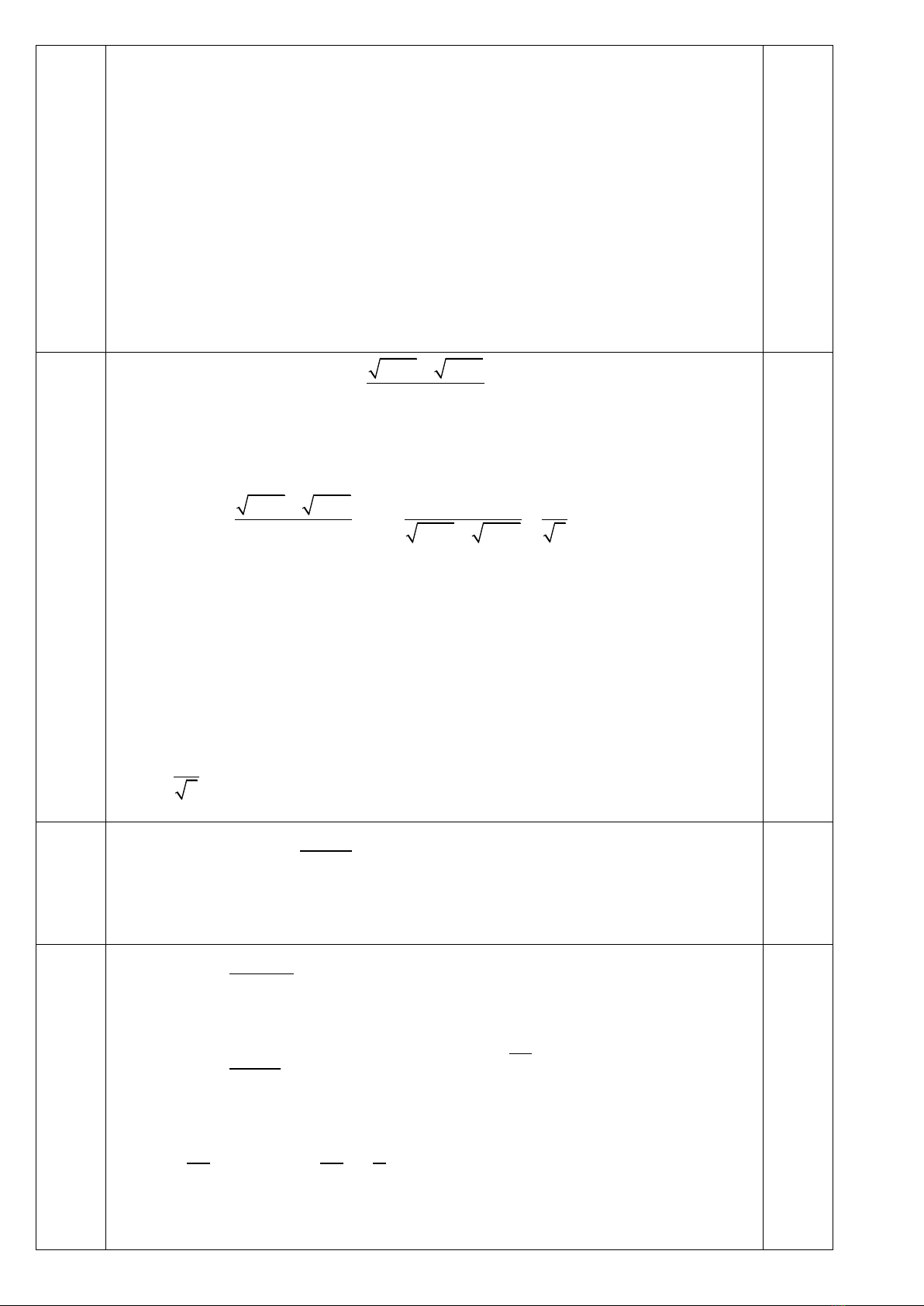
2
3 2 2
(1) 0
( 1) ( 8) ( 2 3) 0
fm
f m m m

11
( 1). (1) 0,
[ 1;1] sao cho ( ) 0.
f f m
x f x
Vậy pt (1) có ít nhất 1 nghiệm với mọi m.
Bài 4
(1đ) Tìm m để hàm số
liên tục trên
[ 2;2]
.
0 0 0
0
2 2 2 1
lim ( ) lim lim 2 2 2
lim ( 2 )
(0)
x x x
x
xx
fx xxx
m x m
fm

Hàm số liên tục trên
[ 2;2]
khi và chỉ khi
00
lim ( ) lim ( ( ) (0)
1
2
xx
f x f x f
m




Bài 5
Cho hàm số
21
() 1
x
y f x x

có đồ thị (C).
a)Viết pt tiếp tuyến tại giao điểm của đồ thị hàm số (C) và đường thẳng
21yx
.
2
3
' '( ) (1 )
y f x x

.
Pthđ giao điểm :
1
21
2 1; ( 1) 2
10
x
xxx
xx
1 1 4
0; '( )
2 2 3
0 1; '(0) 3
x y f
x y f

Tại
1
1;0
2
M



,
42
:33
pttt y x
Tại M2(0;1),
: 3 1pttt y x
b)Viết phương trình tiếp tuyến của đồ thị hàm số (C ) biết tiếp tuyến song song với đường
thẳng
3 1 0xy
.
Gọi M(xo;yo) là tọa độ tiếp điểm. tt song song với (d):
2
0
0
0
31
(1 ) 3
21
43
x
xy
xy
pttt tại M(-2;-1);
11
33
yx
( loại)
pttt tại M(4;-3);
1 13
33
yx
Bài 6
(4đ) Hình chóp S.ABCD có O là tâm của hình thoi ABCD, AB = a, , SA ⊥
(𝐴𝐵𝐶𝐷),
3SA a
. Dựng OK ⊥ SC ( K thuộc SC).
a) Chứng minh
BD
(SAC)
. Tính khoảng cách giữa hai đường thẳng BD và SC.
b) Tính góc tạo bởi đường thẳng SA và mặt phẳng (SBD).
c) Tính khoảng cách từ C đến mặt phẳng (SBD).
d) Tính góc tạo bởi hai mặt phẳng (KBC) và (OBC).
BD
(SAC)
*
Khoảng cách giữa hai đường thẳng BD và SC là OK.
a)
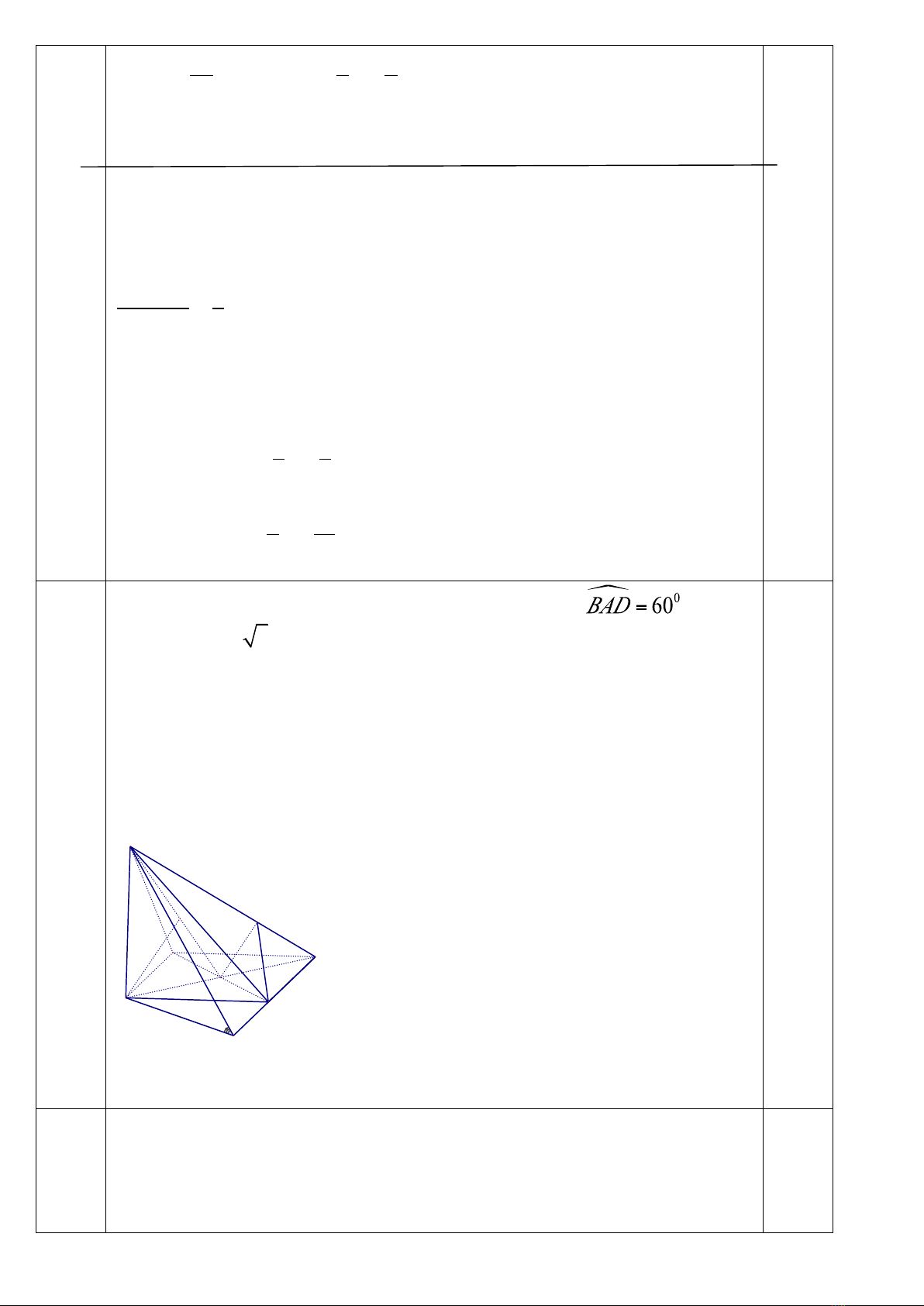
Học sinh chứng minh
O
C
D
A
B
S
H
K
I
* Tam giác SAC có
3SA AC a
. Gọi M là trung điểm SC
Suy ra
1 1 6
2 4 4
a
OK AM SC
b)Tính góc tạo bởi đường thẳng SA và mặt phẳng (SBD).
Xác định SH là hình chiếu vuông góc của SA lên (SBD), suy ra góc
[ ;( )]SA SBD ASH ASO
0
1
tan 26 34'
2
ASO ASO
c)Tính khoảng cách từ C đến mặt phẳng (SBD).
d[C;(SBD)] d[A;(SBD)]
AH (SBD) d[A;(SBD)] AH
2 2 2
1 1 1 15
5
a
AH
AH SA AO
d)Tính góc tạo bởi hai mặt phẳng (KBC) và (OBC).
Xác định đúng
[( );( )] [( );( )]KBC OBC SBC ABC SIA
23
. . 2 4
3
2
ABC
a
AI BC AC BO S
a
AI

SA
tan
SIA
2
AI
[(KBC);(OBC)]
[(SBC);(
ABC)]
SIA
6
0
3
26
'