SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THPT BÁCH VIỆT
_________
Đề thi chính thức
Đề thi có 01 trang
ĐỀ KIỂM TRA CUỐI HỌC KỲ II
NĂM HỌC 2019- 2020
Môn thi: Toán Khối 11
Thời gian làm bài: 90 phút
(không kể thời gian giao đề)
Ngày thi: 27 / 6 /2020
Câu 1: (2 điểm) Tìm các giới hạn sau.
a. 3 2
3
623
lim
3 2
x
x x
x x

b. 1
2 3 1
lim
x
x x
x
c.
4.5 2
lim
3.2 2.5
n
n n
d. 1
2
lim
1
x
x
x
e. 0
1 . 1 1
lim
nm
x
x x
x
Câu 2: ( 1 điểm) Cho hàm số
2
2
3 7 2
,khi 2
( ) 2
1,khi 2
x x x
f x x
mx x
Tìm m để hàm số liên tục tại
2
x
Câu 3: (2 điểm) Tính đạo hàm của các hàm số sau.
a.
1000
4
1 3
4 51
4
y x x x
b.
2 5
y cos( )
1
x
x
c. 4 3
5 2 cos 2
y x x x
d. 10
2
2
siny
x
Câu 4: (1 điểm ) Cho hàm số 3 2
( ) 6 9
y f x x x x
cos đồ thị
( )
C
a. Viết phương trình tiếp tuyến của
( )
C
biết tiếp điểm có hoành độ bằng -2
b. Giải phương trình '
(cosx)=0
f
Câu 5: ( 0,5 điểm ) Cho hàm số
2 2
1
x
y
x
có đồ thị
( )
C
Viết phương trình tiếp tuyến với đồ thị
( )
C
biết tiếp tuyến vuông góc với đường
thẳng
1
y x
Câu 6: (2,5 điểm ) Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA
(ABCD),
SA=
2
a
a.Chứng minh :
(SAC),(SAB) (SAD)
BD
b.Gọi H là hình chiếu vuông góc của A trên SB . Chứng minh
BC AH
c.Gọi O là giao điểm của hai đường chéo hình vuông. Tính góc giữa SO và (ABCD)
d.Tính khoảng cách giữa hai đường thẳng SB và AD
e. Tính khoảng cách từ O đến mặt phẳng ( SBD )
Câu 7.(0,5 điểm ) Chứng minh rằng phương trình 5 4
3 5 2 0
x x x
có ít nhất hai nghiệm
thuộc khoảng (0;2).
-----------HẾT-------------
Thí sinh không được sử dụng tài liệu
Giám thị không giải thích gì thêm
Họ và tên học sinh: ................................................ Số báo danh: ..................... ...................
Chữ ký của giám thị 1: .......................................... Chữ ký của giám thị 2 ..........................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THPT BÁCH VIỆT
_________
Đ
Ề THI CHÍNH THỨC
HƯỚNG DẪN CHẤM THI MÔN TOÁN
KIỂM TRA CUỐI HỌC KỲ II KHỐI 11
NĂM HỌC 2019 – 2020
(Bản Hướng dẫn chấm thi gồm 04 trang)
Câu Nội dung Điểm
Câu 1:
2,5 điểm a.
3
3 2 3
33
2 3
2 3
(6 )
6 2 3
lim lim 6
3 2
3 2 (1 )
x x
x
x x x x
x x x
x x
 
KL:
1 1
1
2 3 1 (2 3 1).(2 3 1)
.lim lim
1( 1).(2 3 1)
( 1)(4 1) 5
lim 4
( 1).(2 3 1)
x x
x
x x x x x x
bxx x x
x x
x x x
KL:
c.
5 2
4.( )
4.5 2 5 5
lim lim 2
2 5
3.2 2.5 3.( ) 2.( )
5 5
n
nn
n n n n
KL:
d. Ta có :
1
1
lim( 2) 1 0
lim(x 1) 0
1 0, 1
x
x
x
x x
1
2
lim
1
x
x
x

e. 0 0
1 . 1 1 1 .( 1 1) 1 1
lim lim( )
n n
m m m
x x
x x x x x
x x x
1 2
1 2
0
1
1
1 .( 1 1)).( 1 1 .. 1 1)
lim( .( 1 1 .. 1 1)
( 1 1).( 1 ... 1))
.( 1 ... 1)
n n
n n n n
m
n n
xn n n
n
m m
n
m
x x x x x
x x x x
x x
n m
x x
KL:
0,5
0,5
0,5
0,5
0,5
Câu 2:
1 điểm Ta có: 2
2 2
3 7 2 (3x 1)(x 2)
lim lim 5
2 2
x x
x x
x x
Mặt khác :
( 2) 4 1
f m
Hàm số liên tục thì :
3
4 1 5
2
m m
KL:
0,5
0,5
Câu 3:
2 điểm
'
4 1000
4 999 3
2
1 3
. ' ( 4 51)
4
1 3 2 3
1000( 4 51) .( )
4
a y x x x
x x x
x x
x
KL:
b.
'
2
2 5 7 2 5
' cos( ) sin( )
1 ( 1) 1
x x
yx x x
KL:
c. 3
'
4 3
4 3
10 3 sin 2
' 5 2 os2x
5 2 os2x
x x x
y x x c x x c
KL:
10 9
2 2 2
9
3 2 2
2 2 2
. ' (sin )' 10.sin (sin )'
40 2 4
.sin .sin
d y
x x x
x x x
KL
0,5
0,5
0,5
0,5
Câu 4:
1 điểm
a. Gọi PTTT có dạng :
0 0 0
'( ).(x x ) ( )
y y x y x
Ta có: 2
' 3 12 9
y x x
Hoành độ tiếp điểm bằng -2 0
2
x
( 2) 50
y
'( 2) 45
y
PTTT:
45( 2) 50 45 40
y x x
KL:
b.
'(cosx)=0
f 2
cos 12cos 9 0
cos 3( )
cos 1
x x
x PTVN
x
cos 1 2 ,x x k k
KL
0,5
0,5
Câu 5:
0,5 điểm
Gọi PTTT có dạng :
0 0 0
'( ).(x x ) ( )
y y x y x
Ta có :
2
2 2 4
' ( )'
1 ( 1)
x
yx x
Vì PTTT vuông góc với y=-x+1 nên ta có:
0 0
2
0
0
2
0
0
4
'( ).( 1) 1 1( 1)
( 1)
1
( 1) 4 3
y x x
x
x
xx
Tại 0
1
x
:
'(1) 1; (1) 0
y y
PTTT:
1
y x
Tại 0
3
x
:
'( 3) 1; ( 3) 4
y y
PTTT:
7
y x
KL:
0,25
0,25
Câu 6:
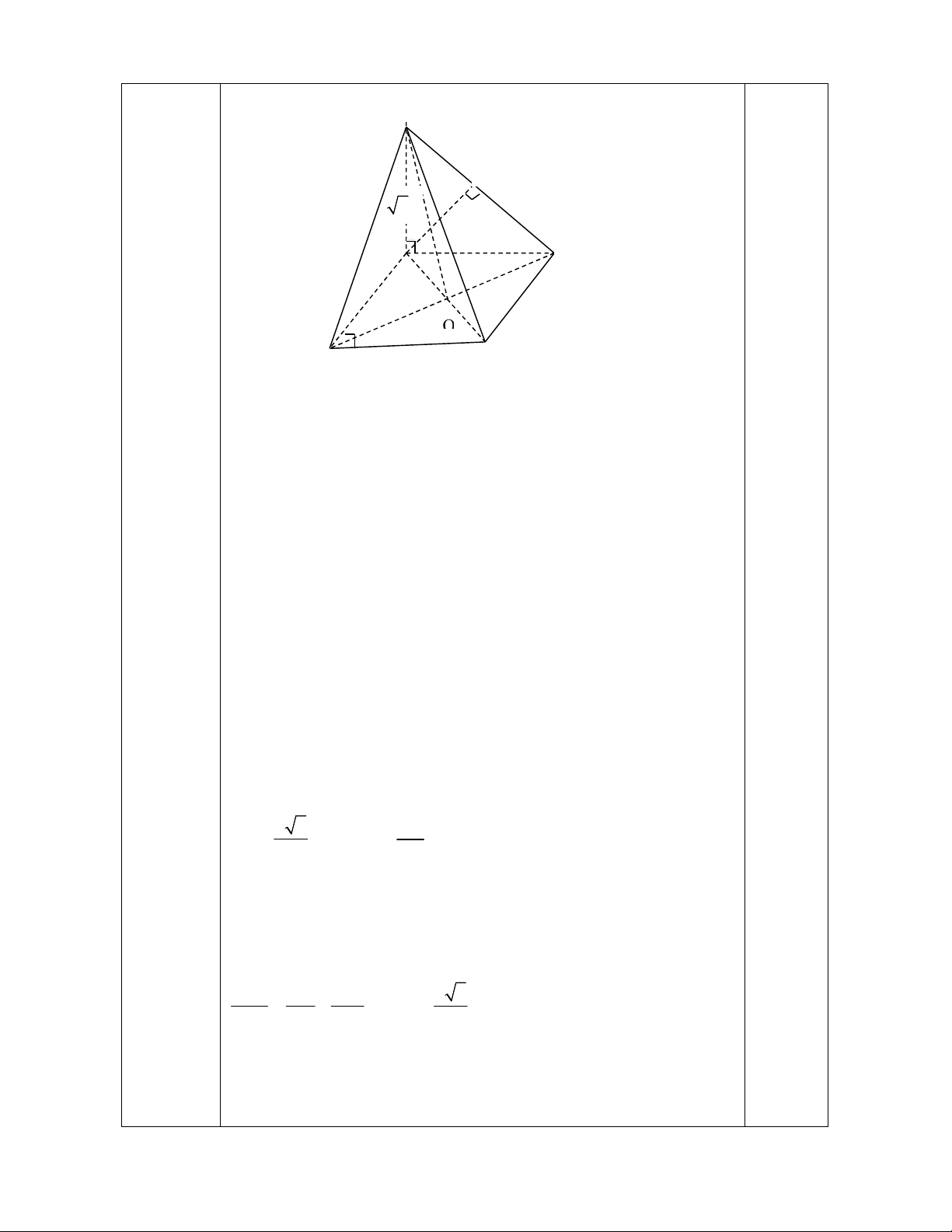
2,5 điểm
a.+) Cm:
( )
BD SAC
Ta có :
BD AC
BD SA
( ABCD là hình vuông, SA là đường cao )
( )
BD SAC
+) cm :
( ) ( )
SAB SAD
: ( )
cm AD SAB
Ta có:
AD SA
AD AB
( ABCD là hình vuông, SA là đường cao )
( )
AD SAB
mà
( ) ( ) ( )
AD SAD SAD SAB
b.cm :
: ( )
BC AH cm BC SAB
Ta có:
BC SA
BC AB
( )
BC SAB
mà ( )
AH SAB BC AH
c. Góc giữa SO và (ABCD)
SA
( )
ABCD
A là hình chiếu của S lên (ABCD)
AO là hình chiếu của SO lên (ABCD)
Góc giữa SO và (ABCD) chính là góc giữa SO và AO
ˆ
SOA
2
2
a
AO
0
ˆ ˆ
tan 2 63
SA
SOA SOA
AO
d.d(SB,AD)
Ta có:
( )
AD BC AD SBC
( , ) ( , ) ( , ) AH
d SB AD d AD SBC d A SBC
Cm:
( )( )
AH SBC cmb
Xét tam giác vuông SAB ta có:
2 2 2
1 1 1 6
3
a
AH
AH SA AB
e.d(O,SBD)
( )
(O,SBD) 0
O BD
BD SBD
d O a
0,25
0,25
0,5
0,5
0,5
0,5
S
A
B
C
D
O
H
a
2
a
Câu 7:
0,5 điểm Đặt 5 4
( ) 3 5 2
f x x x x
thì f(x) liên tục trên R
Ta có:
(0) 2
(1) 1
(2) 8
f
f
f
(0). (1) 2 0
f f
do đó có ít nhất một nghiệm thuộc (0;1)
(1). (2) 8 0
f f
do đó có ít nhất một nghiệm thuộc (1,2)
Mà (0;1) và (1;2) là hai khoảng riêng biệt do đó phương trình đã
cho có ít nhất hai nghiệm thuộc (0,2)
0,5
--- HẾT ---