Đề thi học kì 2 môn Toán lớp 9 năm 2022-2023 có đáp án - Phòng GD&ĐT Hải Lăng

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:5

Thêm vào BST

Báo xấu

7
lượt xem 0
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Vận dụng kiến thức và kĩ năng các bạn đã được học để thử sức với "Đề thi học kì 2 môn Toán lớp 9 năm 2022-2023 có đáp án - Phòng GD&ĐT Hải Lăng" này nhé. Thông qua đề kiểm tra các bạn sẽ được ôn tập và nắm vững kiến thức môn học. Chúc các bạn thi tốt!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Đề thi học kì 2 môn Toán lớp 9 năm 2022-2023 có đáp án - Phòng GD&ĐT Hải Lăng

PHÒNG GD&ĐT HẢI LĂNG ĐỀ THI HỌC KỲ II ĐỀ CHÍNH THỨC Môn: TOÁN 9 Năm học : 2022 - 2023 Thời gian: 90 phút (không kể thời gian giao đề) Câu 1: (1 điểm) 3x  2 y  8 Giải hệ phương trình  (1) 2x  y  3 Câu 2: (2 điểm) Trên cùng một mặt phẳng tọa độ Oxy cho hai đồ thị  P  : y  x 2 và  d  : y  4 x  3 a) Vẽ  P  b) Tìm tọa độ giao điểm của  P  và  d  . Câu 3: (3 điểm) Cho phương trình x 2  2  m  1 x  4m  0 (1), ( m là tham số) a) Giải phương trình (1) với m  2 . b) Chứng tỏ phương trình (1) luôn có nghiệm với mọi m . c) Tìm giá trị của m để phương trình (1) có hai nghiệm x1 , x2 thỏa mãn: x1 1  x2   x2 1  x1   7 . Câu 4: (1 điểm) Khoảng cách giữa hai bến sông A và B là 30km, một canô đi từ bến A đến bến B, nghỉ 40 phút ở bến B rồi quay lại bến A. Kể từ lúc khởi hành đến khi về tới bến A hết tất cả 6 giờ. Hãy tìm vận tốc canô khi nước yên lặng, biết vận tốc của nước chảy là 3km/h. Câu 5: (3 điểm) Từ điểm A ở ngoài đường tròn  O;2cm  . Kẻ hai tiếp tuyến AB, AC và cát tuyến AMN với đường tròn đó ( M nằm giữa A và N ), cho góc BAC có số đo bằng 600 . a) Chứng minh tứ giác ABOC nội tiếp đường tròn. Xác định tâm và bán kính của đường tròn ngoại tiếp tứ giác ABOC . b) Chứng minh: AB 2  AM . AN c) Tính diện tích phần hình giới hạn bởi các đoạn AB, AC và cung nhỏ BC nói trên. ( Cán bộ coi thi không giải thích gì thêm)
HƯỚNG DẪN CHẤM MÔN TOÁN 9 - HỌC KÌ II Câu Nội dung Điểm 3x  2 y  8 Giải hệ phương trình:  (1) 2x  y  3 3x  2 y  8 0,25 Hệ phương trình: (I)   4x  2 y  6 1 7x  14 0,25   (1,0 đ) 3x+ 2y  6 x  2 0,25   6x+ 2y  8 x  2 0,25   y 1 a) Vẽ  P  : y  x 2 + Lập bảng giá trị đúng : 0,5 x -2 -1 0 1 2 2 y=x 4 1 0 1 4 0,5 2 (2,0 đ) + Vẽ đúng đồ thị : b)Tìm tọa độ giao điểm của  P  và  d  . + Pt hoành độ giao điểm của  P  và  d  : x 2  4 x  3  0 0,25 x1  1  y1  1: A  1;1 0,25 + x2  3  y2  9 : B  3;9  0,25 Vậy tọa độ giao điểm của  P  và  d  là A  1;1 ; B  3;9  0,25 Cho phương trình x2 – 2 (m + 1) x + 4m = 0 (1), (m là tham số) 3 a. Giải phương trình (1) với m = 2 (3,0 đ) Thế m = 2 vào (1) ta có phương trình : x2 – 6x + 8 = 0 0,5  '  (3)2  8  1   '  1 0,25
x1 = 3 – 1 = 2 , x 2 = 3 + = 4 0,25 b. Chứng tỏ phương trình : (1) luôn có nghiệm mọi giá trị của m  '  (m 1)2  4m 0,25 m2 + 2m + 1 – 4m = m2 – 2m + 1 0,25 = (m – 1)2  0 với mọi m, do đó phương trình (1) luôn có 0,25 nghiệm thỏa mãn với mọi m c. Tìm giá trị của m để phương trình (1) có hai nghiêm x1, x2 thỏa mãn: x1 ( 1 + x2) + x2 ( 1 + x1) = 7 0,25 Với x1, x2 là hai nghiệm của phương trình (1) ta có:  x1  x2  2(m  1)   x1 x2  4m 0,25 Theo bài ra : x1 ( 1 + x2) + x2 ( 1 + x1) = 7  x1 + x1 x2 + x2 + x1 x2= 7 0,25  x1 + x2 + 2 x1 x2= 7 0,25  2m +2 +8m= 7 0,25 1  10m = 5  m = 2 Gọi vận tốc canô khi nước yên lặng là x (km/h), x > 3 0,25 Vận tốc xuôi dòng là x + 3 (km/h) Vận tốc ngược dòng là x – 3 (km/h) 30 Thời gian canô xuôi dòng là (h) x3 4 30 Thời gian ca nô ngược dòng là (h) 0,25 (1 đ) x3 30 30 2 0,25 Theo đề bài ta có pt:   6 x 3 x 3 3 3 Giải được: x1 = 12 ; x2 = (loại) 4 0,25 Trả lời: Vận tốc ca nô khi nước yên lặng là 12km/h.
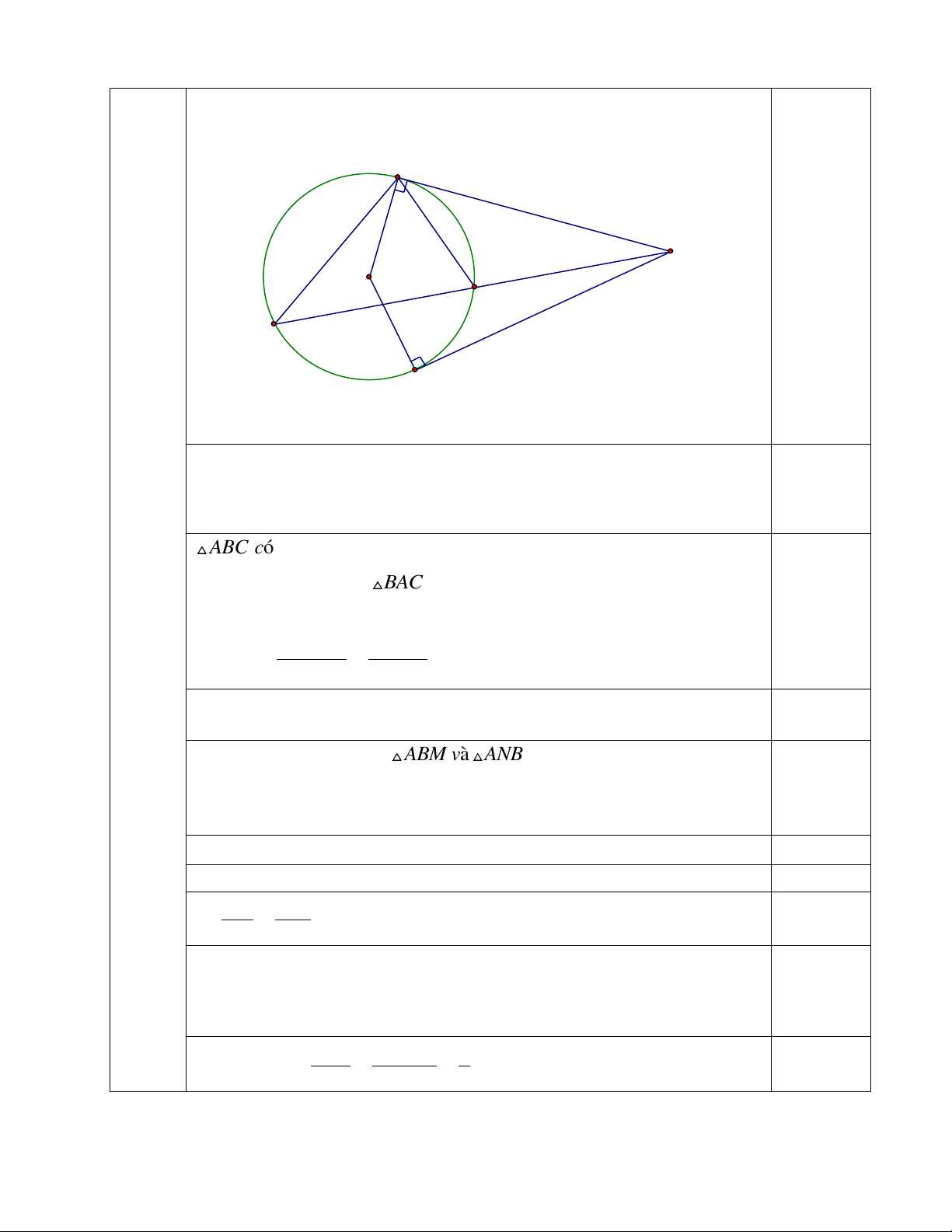
5 (3,0 đ) Vẽ hình: B A O M N C a) Tứ giác ABOC có ABO  ACO  900 (tính chất của tiếp 0,5đ tuyến )  ABO  ACO  1800  Tứ giác ABOC nội tiếp đường tròn ABC có AB  AC (tính chất hai tiếp tuyến giao nhau ) và 0,25đ  BAC  600 suy ra BAC là tam giác đều  ACB  600  AOB  ACB  600 (hai góc nội tiếp cùng chắn cung) OB 2  OA   0  4 cm cos AOB cos 60 Vậy tứ giác ABOC nội tiếp trung đường tròn tâm là trung điểm 0,25đ của OA bán kính bằng 2 cm. b) Xét hai tam giác ABM và ANB . 0,25đ ABM và ANB (góc tạo bởi tia tiếp tuyến và góc nội tiếp cùng chắn cung BM ) A chung 0,25đ Suy ra ABM đồng dạng ANB(g.g) 0,25đ AB AM 0,25đ    AB 2  AM . AN AN AB c) Tứ giác ABOC nội tiếp 0,25đ  BAC  BOC  180 0  BOC  1800  BAC  1800  600  1200  R 2  .4.120 4 0,25đ Squạt OBMC  0  0   (cm 2 ) 360 360 3
2. AB.OB 0,25đ SOBAC  2SOBA   2 3.2  4 3 2 4 12 3  4 0,25đ Scần tìm = SOBAC – Squạt  4 3   3 3 4(3 3   ) 2  cm 3 HS làm theo cách khác nếu đúng vẫn cho điểm tối đa.