PHÒNG GD & ĐT BẮC TRÀ MY
TRƯỜNG PTDTBT THCS
LY TƯ TRONG
KIỂM TRA CUỐI KỲ II
NĂM HOC 2023 - 2024
MÔN: TOÁN – LỚP 9
Thời gian làm bài: 90 phút (Không kể thời gian phát
đề)
(Đề gồm có 02 trang)
I. PHÂ)N TRẮC NGHIỆM (3,0 điểm)
Chon đáp a n đu ng va# ghi va#o giâ y ba#i la#m.
Câu 1: Trong các phương trình sau, phương trình nào là phương trình bậc nhất hai ẩn?
A. 2x – 2y = z. B. –2x + y = 2. C. 2x – yz = 0. D. 0x + 0y = 2.
Câu 2: Cặp số (1; –2) là nghiệm của phương trình nào sau đây?
A. 2x – y = –3. B. x + 4y = 9. C. x – 2y = 5. D. x – 2y = 1.
Câu 3: Biết hệ phương trình
ax y 0
x + by 3
+ =
=
có nghiệm là
x 1
y 1
=
= −
. Các hệ số a, b là
A. a = –1; b = 4. B. a = 1; b = – 4. C. a = –1; b = 2. D. a = 1; b = – 2.
Câu 4: Hàm số
2
2
3
y x
−
=
đồng biến khi
A. x < 0. B. x
0. C. x > 0. D. x ≠ 0.
Câu 5: Cho hàm số y = ax2 (a
0). Xác định hệ số a, biết rằng đồ thị hàm số đi qua
điểm M (-1; 1)
A. a = 2. B. a ≠ 1. C. a = –1. D. a = 1.
Câu 6: Phương trình bậc hai ax2 + bx + c = 0 (a ≠ 0) có biệt thức ∆ (đenta) là
A. ∆ = b2 – ac. B. ∆ = b2 – 4ac. C. ∆ = b2 + 4ac. D. ∆ =
2
b
– 4ac.
Câu 7: Phương trình ax2 + bx + c = 0 (a ≠ 0) có a – b + c = 0 thì hai nghiệm x1, x2 của
phương trình là
A. x1 = 1, x2 =
b
a
−
B. x1 = 1, x2 =
c
a
C. x1 = –1, x2 =
b
a
−
D. x1 = –1, x2 =
c
a
−
Câu 8: Tìm hai số x, y thỏa mãn x > y ; x + y = 2 và xy = – 15
A. x = 3; y = – 5. B. x = –5; y = – 3. C. x = 5; y = – 3. D. x = 5; y = 3.
Câu 9: Độ dài đường tròn (O; 5cm) là
A. 20π (cm). B. 10π (cm). C. 25π (cm). D. 5π (cm).
Câu 10: Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M và tạo thành
ﾷ
0
AMB 50 .
=
Khi đó số đo cung bị chắn bởi góc ở tâm AOB là bao nhiêu?
A. 500. B. 400. C. 1300. D. 800.
Câu 11: Cho ∆MNP nội tiếp đường tròn (O), biết số đo cung nhỏ MN bằng 600 thì số
đo góc
A.
B.
ﾷ
0
PMN 120 .
=
C.
ﾷ
0
MNP 120 .
=
D.
ﾷ
0
MPN 60 .
=
ĐỀ CHÍNH THỨC
Câu 12: Trên hình, hãy chọn đáp án đúng
A.
ﾷ
=
1
BAx
2
sđ
ﾷ
AmB
. B.
ﾷ
BAx
= sđ
ﾷ
BC
.
C.
ﾷ
=
1
BAx
2
(sđ
ﾷ
AmB
- sđ
ﾷ
AnB
). D.
ﾷ
=
1
BAx
2
sđ
ﾷ
AnB
.
B
m
n
O
x
A
II. PHÂ)N TỰ LUẬN (7,0 điểm)
Bài 1. (2,0 điểm)
a) Giải hệ phương trình:
2x + y = 5
x y = 4
−
b) Vẽ đồ thị hàm số y = 2x2.
Bài 2. (2,0 điểm)
Cho phương trình: x2 – 4x + m – 1 = 0 (1).
a) Xác định hệ số a, b, c của phương trình (1). Giải phương trình (1) với m = – 4.
b) Với x1, x2 là nghiệm phương trình (1). Tìm giá trị của m, biết x1 – x2 = 2.
Bài 3. (3,0 điểm)
Cho đường tròn tâm O đường kính AB, vẽ dây CD vuông góc với AB tại H (H nằm giữa
O và B). Trên tia CD lấy điểm E nằm ngoài đường tròn, EB cắt đường tròn tại F (F khác
B), AF cắt CD tại K.
a) Chứng minh tứ giác BFKH nội tiếp.
b) Chứng minh AB.BH = EB.BF.
c) Cho biết AB = 6 cm, AF = 5 cm. Tính diện tích hình quạt tròn BOF ứng với cung nhỏ
BF của đường tròn (O) (kết quả làm tròn đến chữ số thập phân thứ nhất).
Hết
HƯỚNG DẪN CHẤM – ĐỀ KIỂM TRA CUỐI KỲ II
MÔN: TOÁN - LỚP 9
NĂM HỌC: 2023 - 2024
I. PHÂ)N TRẮC NGHIỆM (3,0 điểm)
Mỗi phương a n chon đu ng ghi 0,25 điểm.
Câu 1 2 3 4 5 6 7 8 9 10 11 12
Đáp án B C D A D B D C B C B D
II. PHÂ)N TỰ LUẬN (7,0 điểm)
Bai Đáp án Điểm
Ba)i 1
(2,0 điểm)
a)
Giải phương trình:
2x + y = 5 3x = 9
x y = 4 x y = 4
− −
x 3 x 3
3 y 4 y 1
= =
− = = −
Vậy hệ phương trình có 1 nghiệm duy nhất là
(x; y) = (3; –1).
0,5
0,5
b)
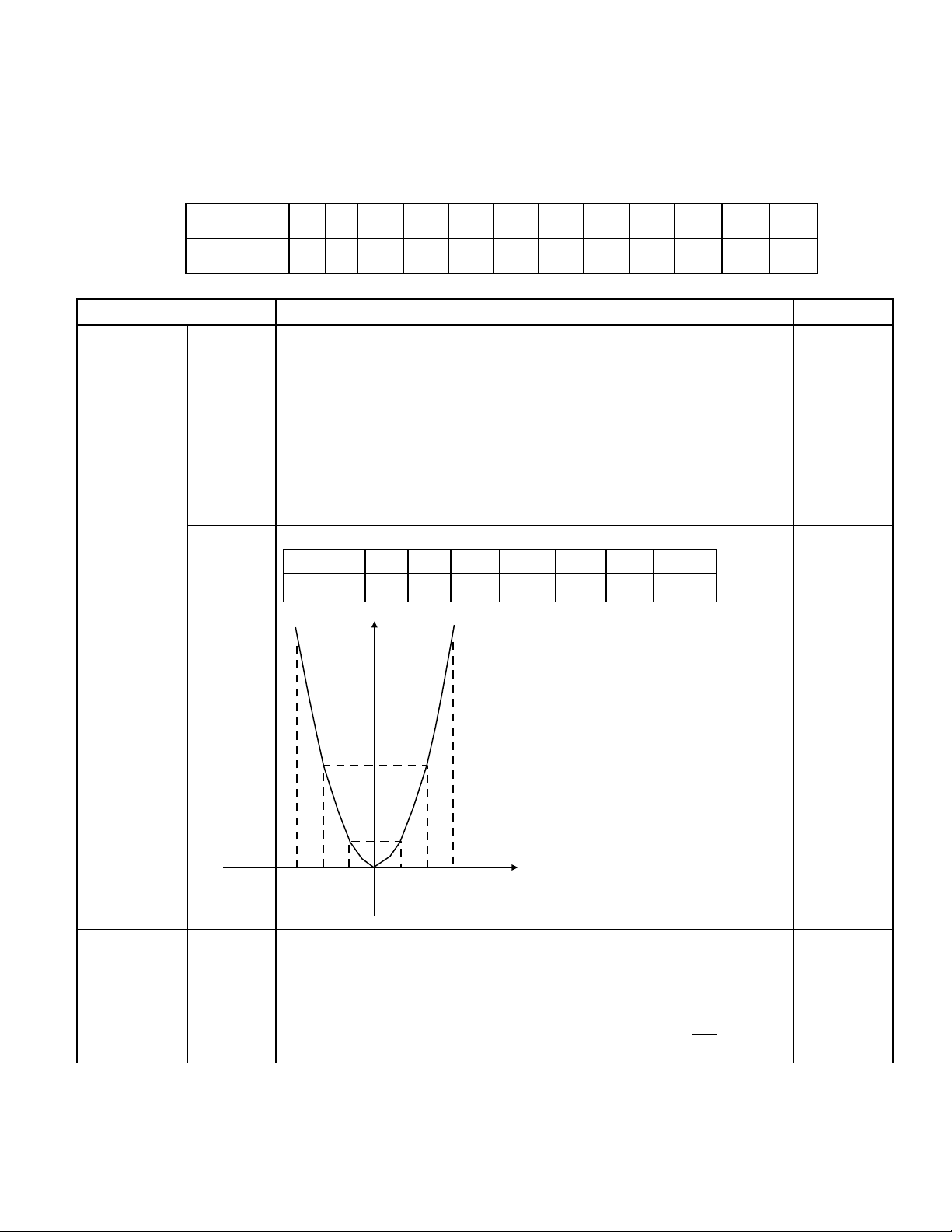
Vẽ đồ thị hàm số y = 2x2
x -3 -2 -1 0 1 2 3
y = 2x218 8 2 0 2 8 18 0,5
0,5
Ba)i 2
(2,0 điểm)
a) Hệ số a = 1; b = –4 ; c = m – 1
Với m = –4 thì phương trình (1) trở thành x2 – 4x – 5 = 0
Phương trình có dạng a – b + c = 0
Vậy phương trình có 2 nghiệm x1 = –1;
2
c
x 5
a
−
= =
0,25
0,25
0,25
0,25
x
y
O
I I I I I I I I I I
-3 -2 -1 1 2 3
–
–
–
–
–
–
–
–
–
–
2
18
8
AA/
b)
Ta có
1 2 1 1
1 2 1 2 2
2 2 6 2 6
4 4 3 4
x x x x
x x x x x
− = = =
+ = + = + =
1
2
3
1
x
x
=
=
Theo hệ thức Vi-et ta có: x1 . x2 = m – 1 hay 3.1 = m –1
m = 4.
0,5
0,5
Ba)i 3
(3,0 điểm)
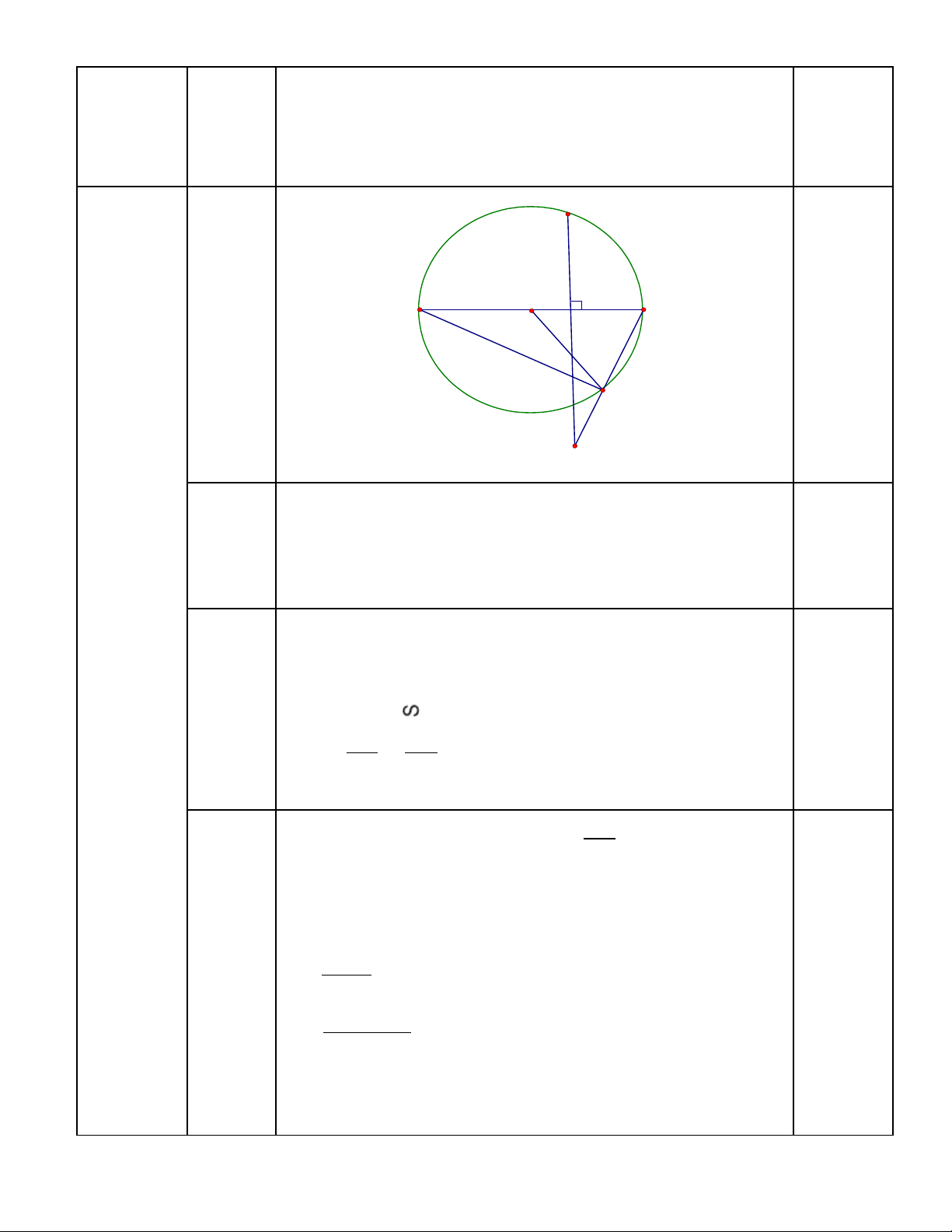
Hình
Vẽ
A
F
E
D
K
H
B
C
O
0,25
a)
Ta có
?
0
BHK 90=
(AB vuông góc với CD tại H)
?
0
BFK 90=
(góc nội tiếp chắn nửa đường tròn)
Suy ra
?
?
0
BHK BFK 180+ =
Do đó tứ giác BFKH nội tiếp.
0,25
0,25
0,25
b)
Xét ∆ABF và ∆EBH có:
?
?
0
AFB BHE 90= =
(cmt)
?
ABE
chung
Do đó ∆ABF ∆EBH (g.g)
Suy ra
AB BF
EB BH
=
(các cạnh tương ứng).
Do đó AB.BH = EB.BF (đpcm).
0,25
0,25
0,25
0,25
c)
Xét ∆AFB vuông tại F, có cos
?
AF
AAB
=
?
A
≈ 33°33’
Suy ra số đo cung nhỏ BF ≈ 67°7’
Diện tích hình quạt là
S =
2
R n
360
p
( )
2 0 2
0
.3 .67 7' 5,3 cm
360
p
ﾷ ﾷ
Vậy diện tích hình quạt tròn BOF ứng với cung nhỏ BF của
đường tròn (O) (kết quả làm tròn đến chữ số thập phân thứ
nhất) là 5,3 cm2.
0,25
0,25
0,25
0,25
Lưu ý: Học sinh có thể giải cách khác nếu đúng thì vẫn ghi điểm tối đa.