PHÒNG GD&ĐT HIỆP ĐỨC KIỂM TRA CUỐI KỲ II – NĂM HỌC 2023-2024
TRƯỜNG TH&THCS LÝ THƯỜNG KIỆT MÔN: TOÁN - LỚP 9
Thời gian: 90 phút (không kể thời gian giao đề)
Họ và tên học sinh:
……………………………….....
Lớp: …………
Điểm
bằng số
Điểm
bằng chữ
Nhận xét và chữ ký
của giám khảo
Chữ ký của
giám thị
MÃ ĐỀ A
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Khoanh tròn chữ cái đứng trước câu trả lời đúng nhất cho mỗi câu hỏi sau đây.
Câu 1. Hệ phương trình nào sau đây là hệ phương trình bậc nhất hai ẩn?
A.
2 6
2 3 0
x y
x y
+ =
− =
B.
2 6
2 3 0
x y
x y
+ =
− =
C.
2
2 6
2 3 0
x y
x y
+ =
− =
D.
2 6
2 3 0
xy y
x xy
+ =
− =
Câu 2. Hàm số y = ax2 (a là tham số) đồng biến khi x < 0 và nghịch biến khi x > 0 nếu
A. a > 0. B. a < 0. C. a = 0. D. a
0.
Câu 3. Đồ thị hàm số y = a x2 là một parapol nhận O là điểm cao nhất khi
A. a = 0. B. a > 0. C. a < 0. D. a
0.
Câu 4. Phương trình ax2 + bx + c = 0 (a ≠ 0) có a
−
b + c = 0 thì phương trình có hai nghiệm là
A.
−
1;
b
a
B.
−
1;
b
a
−
C. –1;
c
a
−
D. 1;
c
a
−
Câu 5. Công thức tính độ dài cung tròn (kí hiệu là l) của đường tròn có bán kính R, số đo cung no là
A.
360
Rn
l
π
=
.B.
180
Rn
l
π
=
.C.
2
360
R n
l
π
=
.D.
2
180
R n
l
π
=
.
Câu 6. Công thức tính diện tích hình tròn (kí hiệu là S) có bán kính R là
A.
2S R
π
=
.B.
2
2S R
π
=
.C.
S R
π
=
.D.
2
S R
π
=
.
Câu 7. Công thức tính diện tích xung quanh (kí hiệu là
xq
S
) của một hình trụ có bán kính đáy r và chiều
cao h là
A.
2
xq
S rh
π
=
.B.
xq
S rh
π
=
.C.
2
2
xq
S r h
π
=
.D.
2
xq
S r h
π
=
.
Câu 8. Tứ giác nào sau đây nội tiếp được đường tròn?
A. Hình bình hành. B. Hình thang. C. Hình vuông. D. Hình thoi.
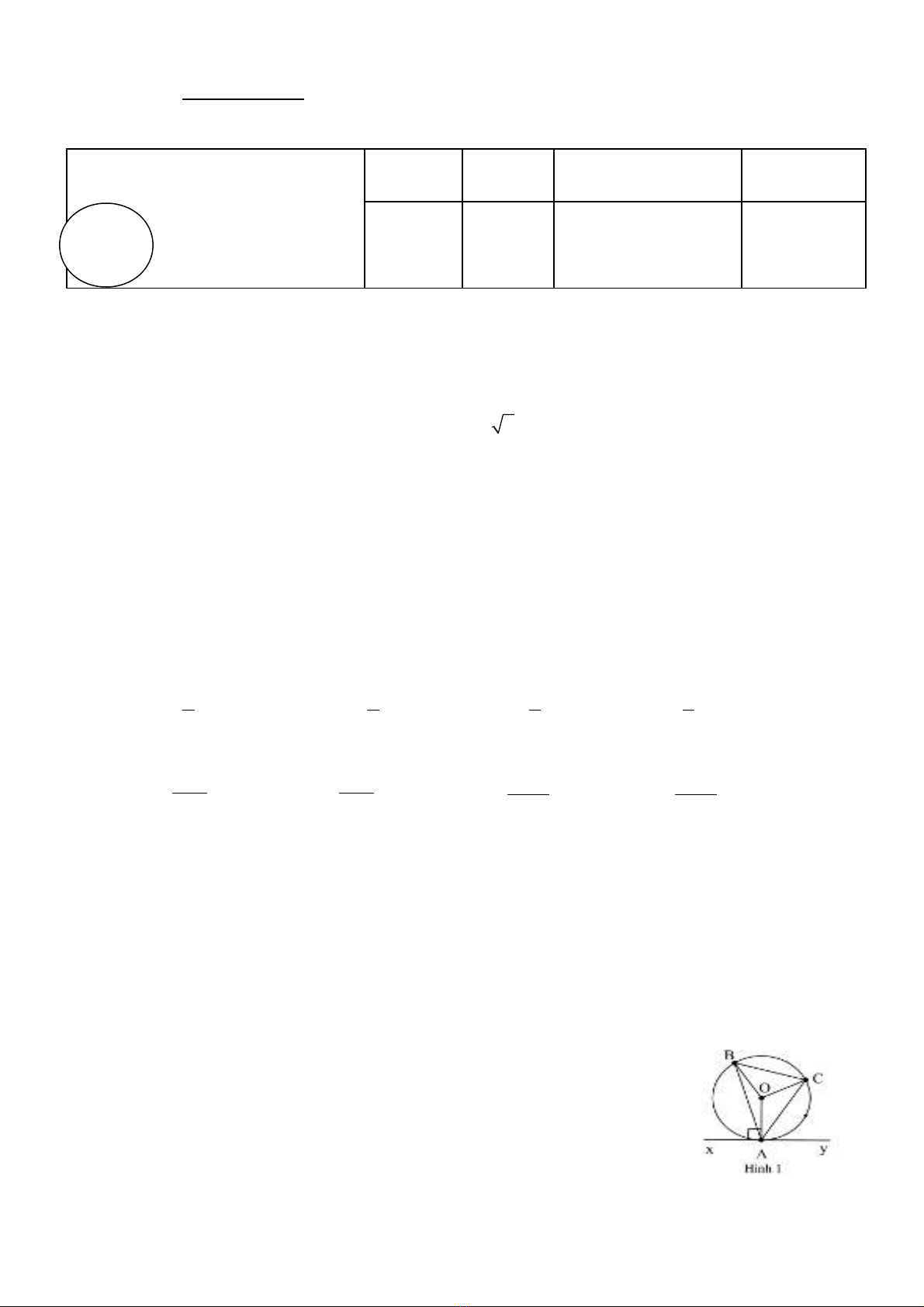
Câu 9. Cho hình 1. GoUc naVo là góc nội tiếp chắn cung nhỏ AB?
A.
?
B A C
.B.
?
A B C
.
C.
?
A OB
.D.
?
A CB
.
PHẦN II. TỰ LUẬN (7,0đ)
Bài 1: (1,0đ)

Viết công thức tính biệt thức ’ của phương trình ax2 + bx + c = 0 (a ≠ 0). Khi nào thì phương
trình bậc hai có hai nghiệm phân biệt? Có nghiệm kép? Vô nghiệm?
Bài 2: (2,0đ)
Cho hàm số y = 0,5x2.
a. Vẽ đồ thị hàm số đã cho.
b. Điểm A(1; 0,5) có thuộc đồ thị hàm số trên hay không? Vì sao?
c. Tìm tất cả các giá trị của m > 0 để đường thẳng y = 2m cắt đồ thị hàm số đã cho tại hai điểm
phân biệt M và N sao cho độ dài MN bằng 4.
Bài 3: (1,0đ)
a. Giải phương trình: (x – 2)(x2 – 4x + 3) = 0.
b. Giải hệ phương trình:
2 7
2
x y
x y
− =
+ =
Bài 4: (3,0đ)
Cho đường tròn (O; R). Từ điểm A nằm ngoài đường tròn kẻ hai tiếp tuyến AB, AC với đường
tròn (B, C là hai tiếp điểm).
a) Chứng minh tứ giác ABOC nội tiếp được một đường tròn.
b) Kẻ cát tuyến ADE (D nằm giữa A và E). Giả sử
ᄋ
50
o
BED =
, hãy tính
ᄋ
sđ BD
,
ᄋ
ABD
.
c) Chứng minh: AD.AE = AB2.
Bài làm:
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
PHÒNG GD&ĐT HIỆP ĐỨC KIỂM TRA CUỐI KỲ II – NĂM HỌC 2023-2024
TRƯỜNG TH&THCS LÝ THƯỜNG KIỆT MÔN: TOÁN - LỚP 9
Thời gian: 90 phút (không kể thời gian giao đề)
Họ và tên học sinh:
……………………………….....
Lớp: …………
Điểm
bằng số
Điểm
bằng chữ
Nhận xét và chữ ký
của giám khảo
Chữ ký của
giám thị
MÃ ĐỀ B
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm)
Khoanh tròn chữ cái đứng trước câu trả lời đúng nhất cho mỗi câu hỏi sau đây.
Câu 1. Hệ phương trình nào sau đây là hệ phương trình bậc nhất hai ẩn?
A.
2
2 6
2 3 0
x y
x y
+ =
− =
B.
2 6
2 3 0
x y
x y
+ =
− =
C.
2
2 6
2 3 0
x y
x y
+ =
− =
D.
2 6
2 3 0
x y
x y
+ =
− =
Câu 2. Hàm số y = ax2 (a là tham số) nghịch biến khi x < 0 và đồng biến khi x > 0 nếu
A. a > 0. B. a < 0. C. a = 0. D. a
0.
Câu 3. Đồ thị hàm số y = ax2 là một parapol nhận O là điểm thấp nhất khi
A. a < 0. B. a > 0. C. a = 0. D. a
0.
Câu 4. Phương trình ax2 + bx + c = 0 (a ≠ 0) có a + b + c = 0 thì phương trình có hai nghiệm là
A.
−
1;
b
a
.B.
−
1;
b
a
−
.C. –1;
c
a
−
.D. 1;
c
a
.
Câu 5. Công thức tính độ dài đường tròn (kí hiệu là C) của đường tròn có bán kính R là
A.
2C R
π
=
.B.
2
2C R
π
=
.C.
C R
π
=
.D.
2
C R
π
=
.
Câu 6. Công thức tính diện tích hình quạt tròn (kí hiệu là Sq) có bán kính R, số đo cung no là
A.
360
q
Rn
S
π
=
.B.
180
q
Rn
S
π
=
.C.
2
360
q
R n
S
π
=
.D.
2
180
q
R n
S
π
=
.
Câu 7. Công thức tính thể tích (kí hiệu là V) của một hình trụ có bán kính đáy r và chiều cao h là
A.
2V rh
π
=
.B.
V rh
π
=
.C.
2
2V r h
π
=
.D.
2
V r h
π
=
.
Câu 8. Tứ giác nào sau đây nội tiếp được đường tròn?
A. Hình bình hành. B. Hình thang. C. Hình chữ nhật. D. Hình thoi.
Câu 9. Cho hình 1. GoUc naVo là góc nội tiếp chắn cung nhỏ AC?
A.
?
B A C
.B.
?
A B C
.
C.
?
A CB
.D.
?
A OB
.
PHẦN II. TỰ LUẬN (7,0đ)
Bài 1: (1,0đ)
Viết công thức tính biệt thức của phương trình ax2 + bx + c = 0 (a ≠ 0). Khi nào thì phương
trình bậc hai có hai nghiệm phân biệt? Có nghiệm kép? Vô nghiệm?
Bài 2: (2,0đ)

Cho hàm số y = - 0,5x2.
a. Vẽ đồ thị hàm số đã cho.
b. Điểm A(1; 0,5) có thuộc đồ thị hàm số trên hay không? Vì sao?
c. Tìm tất cả các giá trị của m < 0 để đường thẳng y = 2m cắt đồ thị hàm số đã cho tại hai điểm
phân biệt M và N sao cho độ dài MN bằng 4.
Bài 3: (1,0đ)
a. Giải phương trình: (3 - x)(x2 – 5x + 4) = 0.
b. Giải hệ phương trình:
3 7
3
x y
x y
− =
− =
.
Bài 5: (3,0đ)
Cho đường tròn (O; R). Từ điểm M nằm ngoài đường tròn kẻ hai tiếp tuyến MN, MP với đường
tròn (N, P là hai tiếp điểm).
a) Chứng minh tứ giác MNOP nội tiếp được một đường tròn.
b) Kẻ cát tuyến MEF (E nằm giữa M và F). Giả sử
ᄋ
50
o
NFE =
, hãy tính
ᄋ
sđ NE
,
ᄋ
MNE
.
c) Chứng minh: ME.MF = MN2.
Bài làm:
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
..........................................................................................................................................................................
PHÒNG GD&ĐT HIỆP ĐỨC HƯỚNG DẪN CHẤM - KIỂM TRA CUỐI KỲ II
TRƯỜNG TH&THCS LÝ THƯỜNG KIỆT MÔN: TOÁN - LỚP 9 - NĂM HỌC 2023 - 2024
Thời gian: 90 phút (không kể thời gian giao đề)
MÃ ĐỀ A
PHẦN I. TRẮC NGHIỆM KHÁCH QUAN (3,0 điểm):
Điểm phần trắc nghiệm bằng số câu đúng chia cho 3 (lấy hai chữ số thập phân)
Câu 1 2 3 4 5 6 7 8 9
Đ/án A B C C B D A C D
HSKT: Làm đúng được từ 5 câu trắc nghiệm trở lên ghi điểm 3.
PHẦN II. TỰ LUẬN (7,0 điểm)
Bài Đáp án Điểm
1
1,0đ
Viết công thức tính biệt thức ’ của phương trình ax2 + bx + c = 0 (a ≠
0). Khi nào thì phương trình bậc hai có hai nghiệm phân biệt? Có
nghiệm kép? Vô nghiệm?
HSKT: nêu đúng công thức ghi 0,5đ; nêu đúng một điều kiện ghi 0,5đ; làm
đúng bài 1 ghi 1đ.
2
' b' ac
∆ = −
với
'2
b
b=
0,25đ
Phương trình bậc hai có hai nghiệm phân biệt khi ’ > 0 0,25đ
Phương trình bậc hai có nghiệm kép khi ’ = 0 0,25đ
Phương trình bậc hai vô nghiệm khi ’ < 0 0,25đ
2
2,0đ
Cho hàm số y = 0,5x2.
a. Vẽ đồ thị hàm số đã cho.
b. Điểm A(1; 0,5) có thuộc đồ thị hàm số trên hay không? Vì sao?
c. Tìm tất cả các giá trị của m > 0 để đường thẳng y = 2m cắt đồ thị hàm
số đã cho tại hai điểm phân biệt M và N sao cho độ dài MN bằng 4.
HSKT: lập được bảng của câu a ghi 0,5đ; vẽ được đồ thị ghi 0,5đ; xác định
được A thuộc đồ thị ghi 0,5đ; làm đúng câu a và b ghi 1đ.
2a
x -4 -2 0 2 4
y 8 2 0 2 8 0.25đ
0,25đ
2b Với x = 1 =>
2 2
0,5 0,5.1 0,5y x= = =
0,25đ
Vậy điểm A(1; 0,5) thuộc đồ thị hàm số trên 0,25đ
2c Phương trình hoành độ giao điểm của đồ thị y = 0,5x2 và đường thẳng y =
2m là: 0,5x2 = 2m <=> 0,5x2 – 2m = 0
HSKT: làm đúng bước này ghi 0,5đ.
0,1đ












![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



