UBND QUẬN BÌNH THẠNH
TRƯỜNG THCS LAM SƠN
ĐỀ THAM KHẢO
KIỂM TRA CUỐI HỌC KỲ II
NĂM HỌC: 2024 – 2025
MÔN: TOÁN – LỚP: 9
Thời gian làm bài: 90 phút
I. TRẮC NGHIỆM KHÁCH QUAN: (3,0 điểm)
Hãy chọn đáp án đúng nhất trong các đáp án sau:
Câu 1: Trong các điểm sau, điểm nào thuộc đồ thị hàm số
2
:Py x
?
A.
( 1; 1)
. B.
(1; 1)
. C.
(2; 3)
. D.
(1; 2)
.
Câu 2: Phương trình nào sau đây là phương trình bậc hai một ẩn ?
A.
2
3 4 10xx 
B.
C.
2
2 30x xy 
D.
2
0 7 50xx 
Câu 3: Gọi S là tổng và P là tích 2 nghiệm của phương trình
2
2 5 30xx− + +=
, khi đó:
A.
3S
,
5
3
P
B.
35
;
22
SP

C.
3; 5SP
. D.
53
;
22
SP

Câu 4: Hãy chọn câu đúng:
A. Phương trình
27 80xx 
có nghiệm kép
B. Phương trình
2
5 12 4 0xx 
vô nghiệm
C. Phương trình
290xx
có hai nghiệm phân biệt
D. Phương trình
2
3 20xx
có hai nghiệm phân biệt
Câu 5: Nghiệm của phương trình 3x2 – 8x + 5 = 0 là:
A.
12
5
1; 3
xx=−=
B.
12
5
1; 3
xx=−=−
C.
12
5
1; 3
xx= = −
D.
12
5
1; 3
xx= =
Câu 6: Một người đi xe máy từ A đến B với bận tốc 25km/h. Lúc về người đó đi với vận tốc 40km/h
nên thời gian về ít hơn thời gian đi là 20 phút. Tính quãng đường AB.
A. 50 km B. 60 km C. 40 km D. 70 km
Câu 7: Trong các phát biểu sau phát biểu nào sai ?
A. Hình vuông nội tiếp đường tròn. B. Mọi tứ giác đều nội tiếp đường tròn.
C. Hình chữ nhật là tứ giác nội tiếp.
D. Tổng số đo hai góc đối trong tứ giác nội tiếp bằng 1800.
Câu 8. Các phép quay có thể có với một đa giác đều tâm O là
A. Phép quay thuận chiều và phép quay đảo chiều.
B. Phép quay thuận chiều và phép quay ngược chiều.
C. Phép quay xuôi chiều và phép quay đảo chiều.
D. Phép quay xuôi chiều và phép quay ngược chiều.
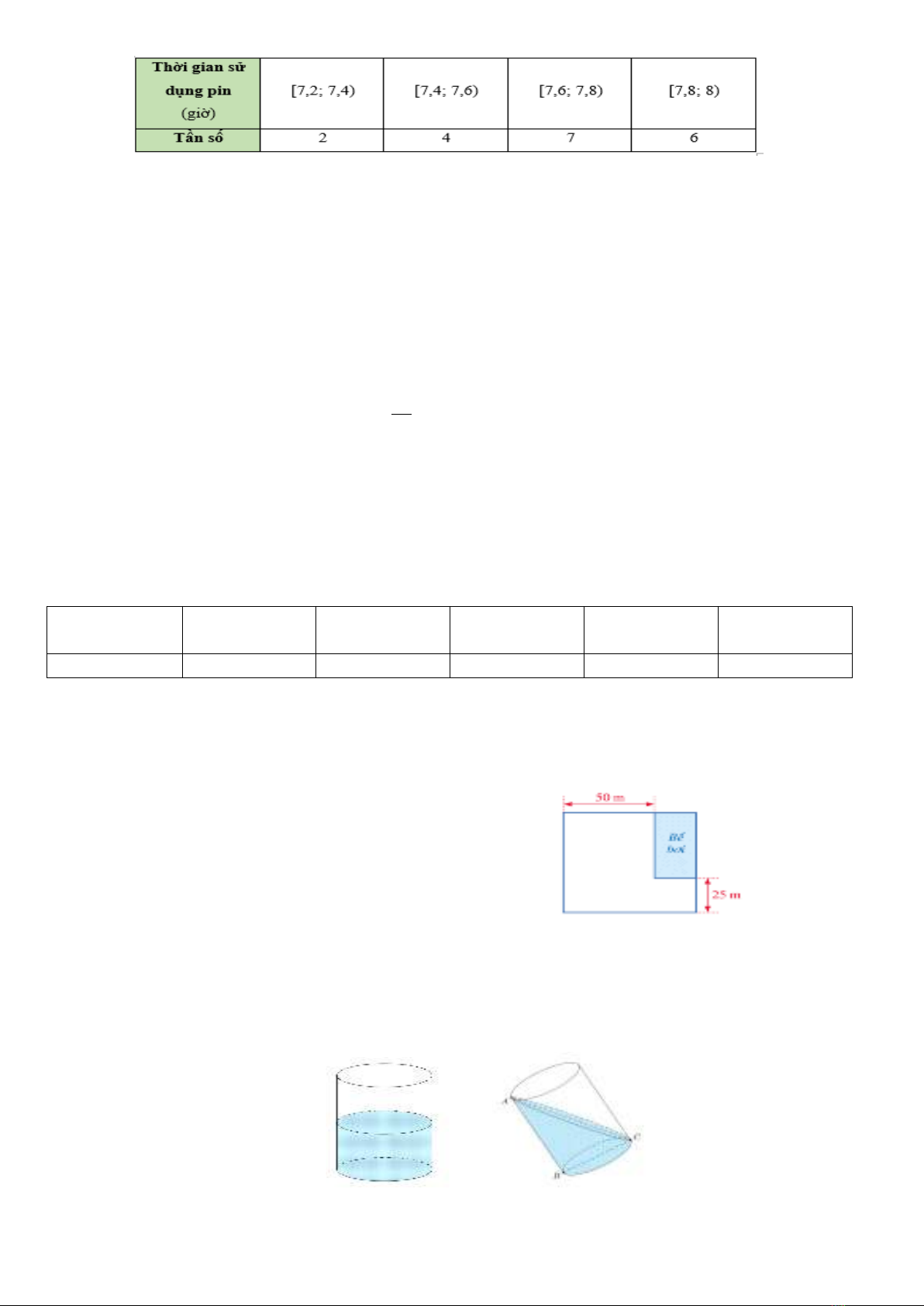
Câu 9. Một doanh nghiệp sản xuất xe ô tô khảo sát lượng xăng tiêu thụ trên 100 km của một số loại
xe ô tô trên thị trường. Kết quả khảo sát 100 chiếc xe được biểu diễn trong hình bên. Tần số tương
đối của số lượng xe ô tô tiêu thụ dưới 5 lít xăng cho 100 km là
A. 24% B. 39% C. 61% D. 76%
Câu 10. Kết quả khảo sát thời gian sử dụng liên tục (đơn vị: giờ) từ lúc sạc đầy cho đến khi hết pin
của một số máy vi tính cùng loại được thống kê lại ở bảng sau:. Cỡ mẫu của cuộc khảo sát là
A. 18 B. 19 C. 20 D. 22
Câu 11. Trong một hình trụ
A. độ dài của đường sinh là chiều cao của hình trụ.
B. đoạn nối hai điểm bất kì trên hai đáy là đường sinh.
C. chiều cao là độ dài đoạn nối hai điểm bất kì trên hai đáy.
D. hai đáy có độ dài bán kính bằng nhau.
Câu 12. Hình nón có chiều cao 3 cm, bán kính đáy 4 cm, thì độ dài đường sinh là
A. 3 cm. B. 4 cm. C. 7 cm. D. 5 cm.
II. PHẦN TỰ LUẬN (7,0 ĐIỂM)
Bài 1. [TH] (1,0 điểm).
a) Vẽ đồ thị (P) của hàm số
=
2
4
x
y
b) Tìm những điểm A thuộc (P) có tung độ gấp đôi hoành độ ?
Bài 2. [VD] (1,0 điểm). Cho phương trình 2x2 – 3x – 2 = 0
Không giải phương trình. Gọi x1, x2 là hai nghiệm của phương trình. Hãy tính giá trị của biểu thức
( )
21
2
21 xx3xx2A+−=
Bài 3. [TH] (0,75 điểm). Một số bài toán về thống kê.
Một quán giải khát thống kê thời gian ( đơn vị: phút) mà 64 hành khách ở tại quán. Kết quả được ghi
lại ở bảng tần số ghép nhóm như sau:
Thời gian
(phút)
[0; 10)
[10; 20)
[20; 30)
[30; 40)
[40; 50)
Tần số
24
16
12
8
4
a) Hãy lập bảng tần số tương đối ghép nhóm cho mẫu số liệu trên.
b) Hãy vẽ biểu đồ tần số tương đối ghép nhóm dạng cột biểu diễn số liệu trên.
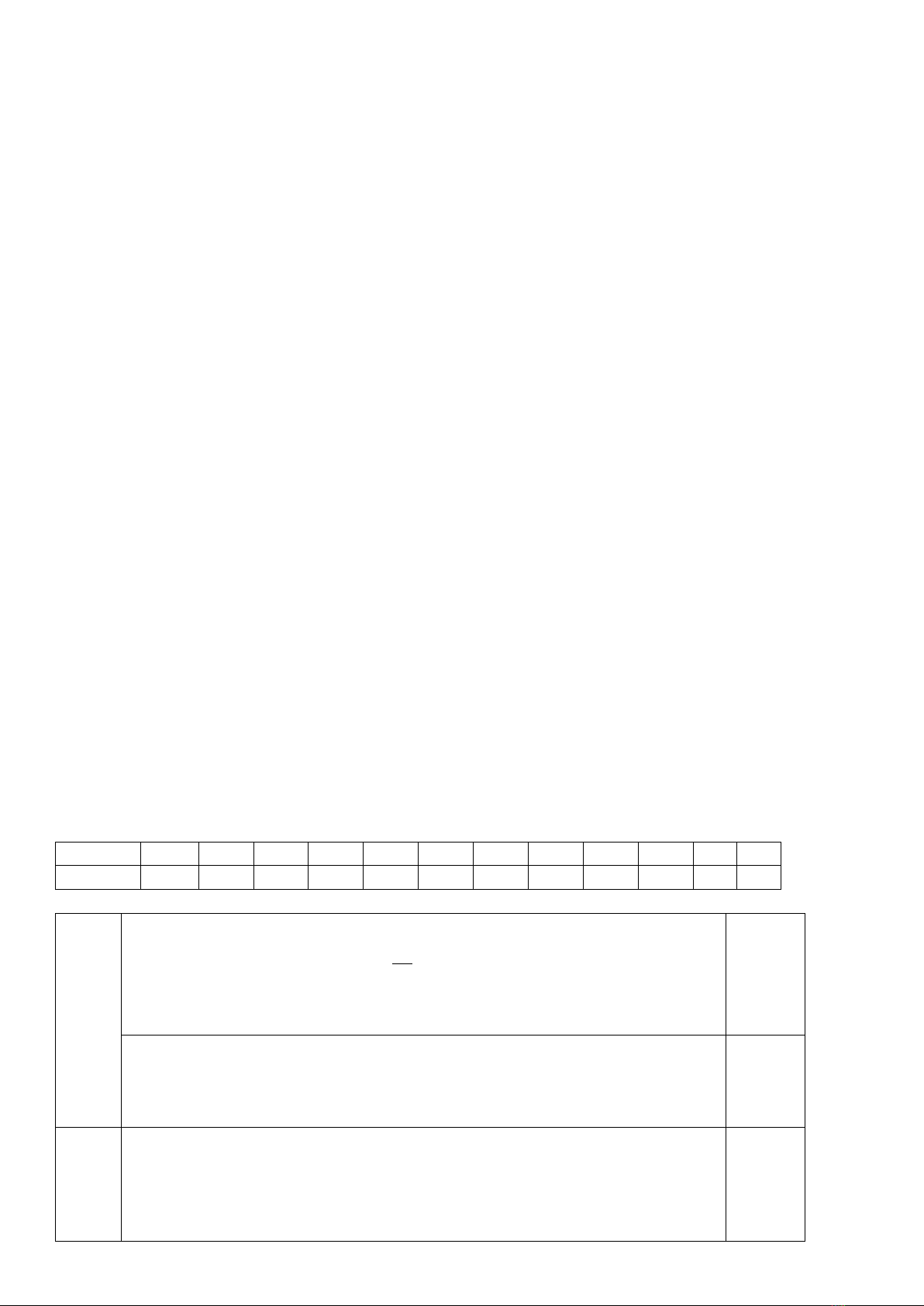
Bài 4. (0,75 điểm) [TH] Trên một khu đất có dạng hình vuông, người ta dành một mảnh đất
có dạng hình chữ nhật ở góc của khu đất để làm bể bơi (như hình vẽ). Tính độ dài cạnh của
khu đất ban đầu, biết diện tích của bể bơi bằng 1 250 m2.
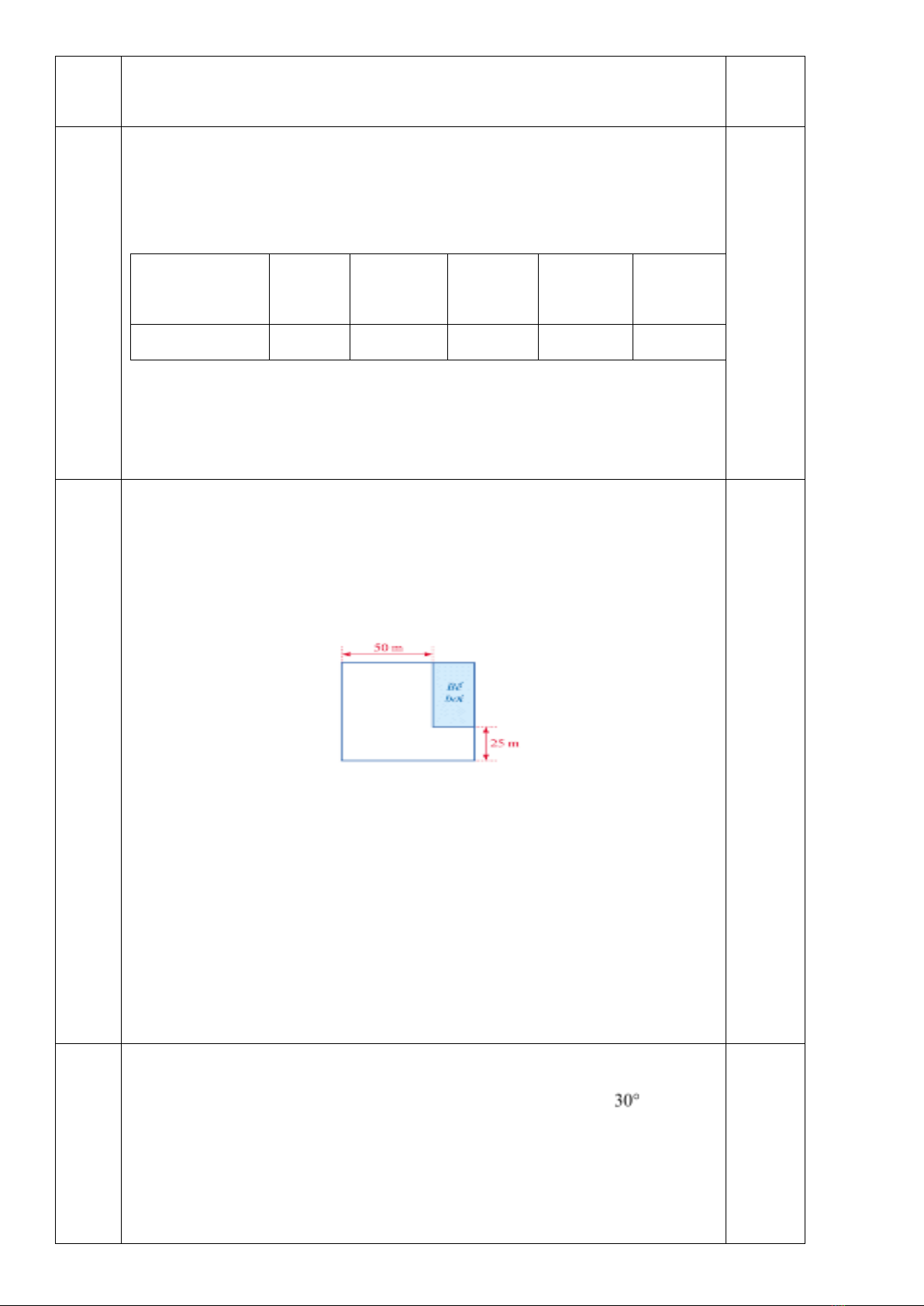
Bài 5: [ VD] (1 điểm) . Đổ nước vào một chiếc thùng hình trụ có bán kính đáy là 20 cm. Nghiêng
thùng cho mặt nước chạm vào miệng cốc và đáy cốc (như hình vẽ) thì mặt nước tạo với đáy cốc một
góc 300.
a) Tính chiều cao của chiếc thùng hình trụ. b) Tính thể tích của chiếc thùng?
(Kết quả làm tròn hai chữ số thập phân)
Bài 6. (2,5 điểm). Từ một điểm A nằm ngoài đường tròn (O; R), kẻ hai tiếp tuyến AB, AC với (O;
R) (B và C là hai tiếp điểm).
a) Chứng minh OA vuông góc với BC và AB2 = AH. AO.
b) Vẽ đường kính BD. Đường thẳng qua O và vuông góc với AD cắt tia BC tại E.
Chứng minh OD2 = OG. OE
c) Nếu cho biết OA = 10cm và R = 5cm. Tính phần diện tích mặt phẳng giới hạn bởi AB, AC và
cung nhỏ BC của (O; R) (làm tròn tới phần thập phân thứ nhất)
HƯỚNG DẪN CHẤM KIỂM TRA CUỐI HỌC KỲ II
I: TRẮC NGHIỆM (Mỗi câu đúng được 0,25 điểm)
Câu
1
2
3
4
5
6
7
8
9
10
11
12
Đáp án
B
A
D
D
D
A
B
B
B
B
A
D
Phần 2: Tự luận (7 điểm)
1
Bài 1. [TH] (1,0 điểm).
a) Vẽ đồ thị (P) của hàm số
=
2
4
x
y
Lập bảng giá trị đúng
Vẽ đồ thị
0,25
0,25
b) Tìm những điểm A thuộc (P) có tung độ gấp đôi hoành độ ?
Tìm được x = 0 và x = 8
Kết luận
0,25
0,25
2
Bài 2. [VD] (1,0 điểm). Cho phương trình 2x2 – 3x – 2 = 0
Không giải phương trình. Gọi x1, x2 là hai nghiệm của phương trình. Hãy
tính giá trị của biểu thức
( )
21
2
21
xx3xx2A+−=
Tính được S, P
Rút gọn A
Tính giá trị A đúng
0,5
0,25
0,25
3
Bài 3. [TH] (0,75 điểm). Một số bài toán về thống kê.
Một quán giải khát thống kê thời gian ( đơn vị: phút) mà 64 hành khách
ở tại quán. Kết quả được ghi lại ở bảng tần số ghép nhóm như sau:
Thời gian
(phút)
[0; 10)
[10; 20)
[20; 30)
[30; 40)
[40; 50)
Tần số
24
16
12
8
4
a) Hãy lập bảng tần số tương đối ghép nhóm cho mẫu số liệu trên.
b) Hãy vẽ biểu đồ tần số tương đối ghép nhóm dạng cột biểu diễn số liệu
trên.
0,5
0,25
4
Bài 4. (0,75 điểm) [TH] Trên một khu đất có dạng hình vuông, người
ta dành một mảnh đất có dạng hình chữ nhật ở góc của khu đất để
làm bể bơi (như hình vẽ). Tính độ dài cạnh của khu đất ban đầu, biết
diện tích của bể bơi bằng 1 250 m2.
Gọi độ dài cạnh của khu đất có dạng hình vuông là x (m) (x > 50).
Khi đó, mảnh đất dạng hình chữ nhật để làm bể bơi có các kích thước
lần lượt là x – 50 (m), x – 25 (m).
Do đó, diện tích của mảnh đất đó là: (x – 50)(x – 25) (m2).
Theo bài, diện tích của bể bơi bằng 1 250 m2 nên ta có phương trình:
(x – 50)(x – 25) = 1 250.
x2 – 75x = 0
x(x – 75) = 0
x = 0 hoặc x = 75.
Do x > 50 nên x = 75.
Vậy độ dài cạnh của khu đất là 75 m.
0,25
0,25
0,25
5
Bài 5: [ VD] (1 điểm) . Đổ nước vào một chiếc thùng hình trụ có bán
kính đáy là 20 cm. Nghiêng thùng cho mặt nước chạm vào miệng cốc và
đáy cốc (như hình vẽ) thì mặt nước tạo với đáy cốc một góc .
a) Tính chiều cao của chiếc thùng hình trụ.
b) b) Tính thể tích của chiếc thùng?
(Kết quả làm tròn hai chữ số thập phân)
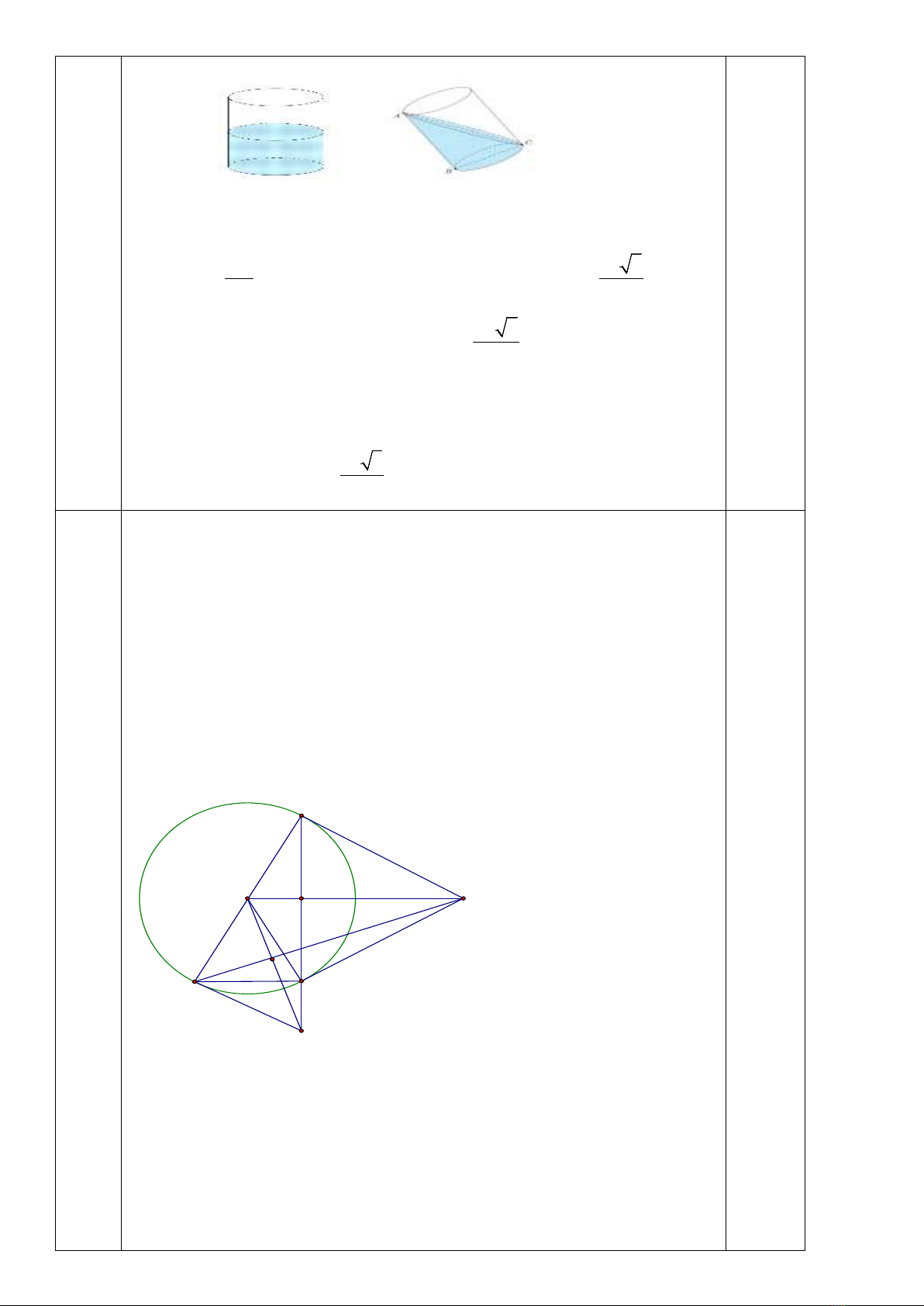
a) Tính chiều cao của chiếc thùng hình trụ.
Xét
∆ABC
vuông tại B ta có:
40 3
tan( ) tan( ). tan(30 ).(20.2) 3
AB
ACB suy ra AB ACB BC
BC
= = =°=
Vậy chiều cao thùng hình trụ là:
40 3
3
h AB= =
b) Tính thể tích của chiếc thùng? (Kết quả làm tròn hai chữ số thập phân)
Thể tích của chiếc thùng là:
22 3
40 3
.(20) . 29020,79
3
V r h cm
ππ
= = ≈
0.5đ
0.25đ
0.25đ
6
Bài 6. (2,5 điểm). Từ một điểm A nằm ngoài đường tròn (O; R), kẻ hai
tiếp tuyến AB, AC với (O; R) (B và C là hai tiếp điểm).
a) Chứng minh OA vuông góc với BC và tứ giác ABOC nội tiếp
b) Vẽ đường kính BD. Đường thẳng qua O và vuông góc với AD cắt tia
BC tại E.
Chứng minh OD2 = OG. OE
b) Nếu cho biết OA = 10cm và R = 5cm. Tính phần diện tích mặt phẳng
giới hạn bởi AB, AC và cung nhỏ BC của (O; R) (làm tròn tới phần thập
phân thứ nhất)
a) Chứng minh OA vuông góc với BC
Tứ giác ABOC nội tiếp
b) Chứng minh được: OB2 = OH. OA
OH. OA = OG. OE
OB = OD
⇒ OD2 = OG. OE
0.5đ
0.5đ
0.25đ
H
G
C
B
O
E
A
D