UBND QUẬN BÌNH THẠNH
TRƯỜNG THCS PHÚ MỸ
ĐỀ ĐỀ NGHỊ
KIỂM TRA CUỐI HỌC KỲ II
NĂM HỌC: 2024 – 2025
MÔN: TOÁN – LỚP: 9
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
I. PHẦN TRẮC NGHIỆM (3,0 Điểm)
Câu 1. Điểm nào sau đây thuộc đồ thị của hàm số
2
1
2
yx= −
A.
( )
4; 4−
B.
( )
4; 8−−
C.
( )
4;8−
D.
( )
4;4
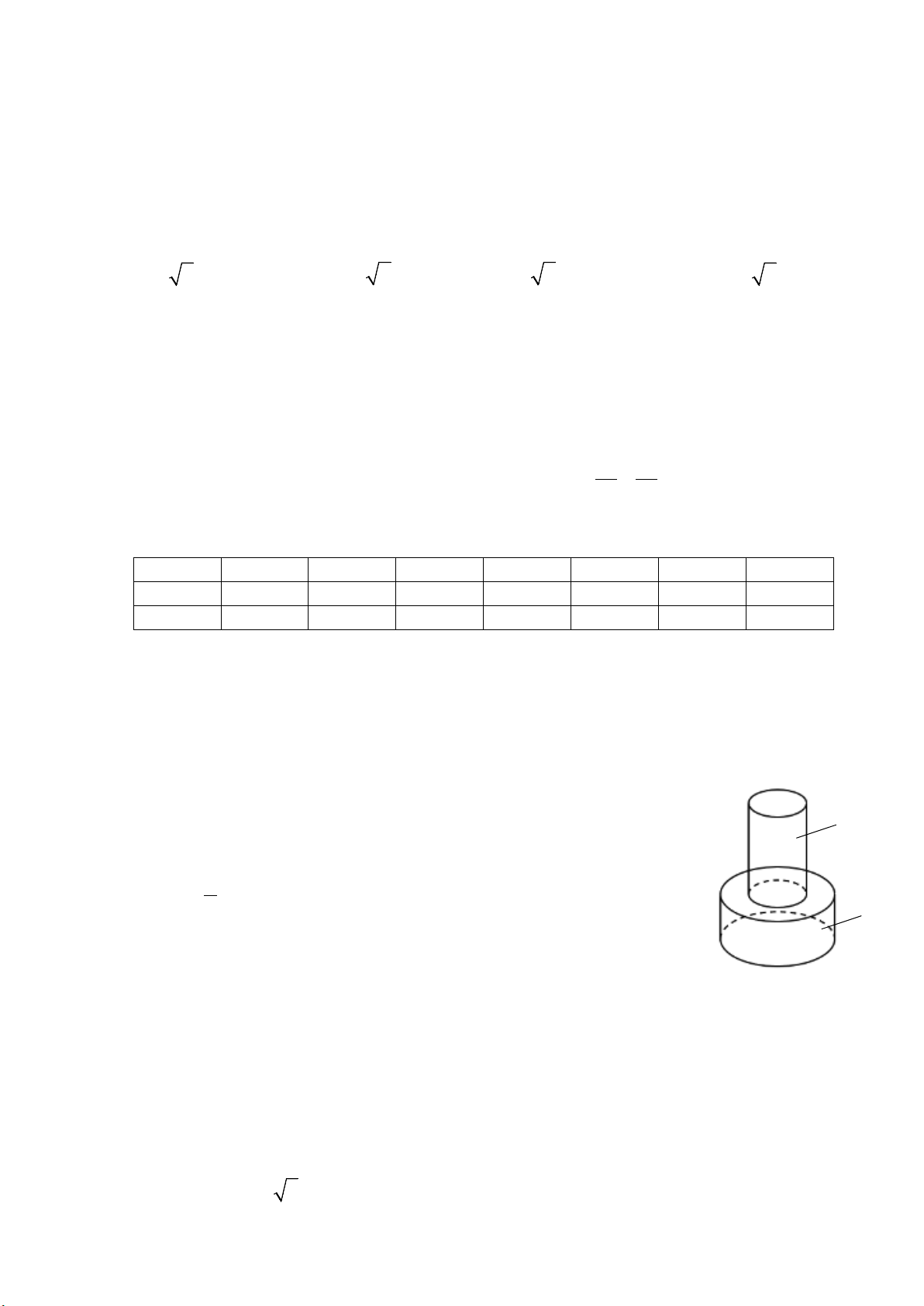
Câu 2. Cho hàm số
2
y ax=
có đồ thị như hình vẽ bên. Hàm số đó là
A.
2
2.yx=
B.
C.
2
.yx= −
D.
2
.yx=
`
Câu 3. Phương trình nào dưới đây là phương trình bậc hai một ẩn?
A.
42
2 0.xx−=
B.
3
3 0.x+=
C.
2 3 0.x−=
D.
2
2 3 0.xx− −=
Câu 4. Cho phương trình
( )
2
00ax bx c a+ += ≠
có biệt thức
24b ac∆= −
. Phương trình đã cho
vô nghiệm khi
A.
0∆<
B.
0∆>
C.
0∆≥
D.
0∆≤
Câu 5. Gọi
12
,xx
là hai nghiệm của phương trình
2
3 20xx− +=
khi đó ta có
A.
1 2 12
3; 2.x x xx+= =
B.
1 2 12
3; 2.x x xx+=− =
C.
1 2 12
3; 2.x x xx+= =−
D.
1 2 12
3; 2.x x xx+=− =−
Câu 6. Cho bảng khảo sát về chiều cao học sinh trong lớp như sau:
Chiều cao (cm)
)
150; 155
)
155; 160
)
160; 165
)
165; 170
)
170; 175
Số học sinh
12
18
8
3
1
Bảng số liệu ghép nhóm trên có số nhóm số liệu là
A.
40
B.
4
C.
5
D.
6
Câu 7. Thời gian hoàn thành một sản phẩm (tính bằng phút) của một số công nhân trong một tổ
được biểu diễn ở biểu đồ dưới đây:
Thời gian hoàn thành một sản phẩm của công nhân chủ yếu là
A. 5 phút. B.17 phút. C. 18 phút và 20 phút. D. 20 phút và 22
phút.
Câu 8. Tích của hai số tự nhiên liên tiếp bằng 56.Khi đó số bé là
A. 14 B.7 C. 6 D. 8
Câu 9. Tứ giác nội tiếp đường tròn là
A. tứ giác có bốn đỉnh nằm trên đường tròn đó.
B. tứ giác một đỉnh nằm trên đường tròn đó.
C. tứ giác có tổng số đo hai góc đối nhau bằng
90 .°
D. tứ giác có ba đỉnh nằm trên đường tròn đó.
3
5 5
4
0
1
2
3
4
5
6
16 phút 18 phút 20 phút 22 phút
Tần số
Thời gian
Thời gian hoàn thành một sản phẩm
của một số công nhân trong một tổ
Câu 10. Phép quay thuận chiều
α
°
tâm
O
biến điểm
A
khác điểm O thành điểm
B
thuộc
đường tròn (O; OA) sao cho khi tia OA quay thuận chiều kim đồng hồ đến tia OB thì điểm
A
tạo nên cung
AB
có số đo bằng
A.
α
°
B.
α
−°
C.
90
α
°− °
D.
180
α
°− °
Câu 11. Một hình trụ có bán kính đáy là 10 cm, chiều cao bằng 12 cm.
Diện tích toàn phần của hình trụ đó là
A.
2
120 cm
π
B.
2
200 cm
π
C.
2
240 cm
π
D.
2
440 cm
π
Câu 12. Cho hình nón có đường kính đáy là 20 cm, chiều cao là 10 cm. Độ dài đường sinh của
hình nón đó là
A.
10 3 cm
B.
20 2 cm
C.
10 2 cm
D.
20 3 cm
II. PHẦN TỰ LUẬN (7,0 Điểm)
Bài 1:(1.0 điểm) Cho hàm số
2
2yx= −
có đồ thị là (P)
a) Vẽ (P) trên mặt phẳng tọa độ Oxy
b) Tìm tọa độ những điểm M thuộc (P) có tung độ bằng - 8
Bài 2: :(1.0 điểm) Cho phương trình:
2
2 5 40xx− −=
a) Chứng minh phương trình có 2 nghiệm phân biệt
12
,xx
b) Không giải phương trình, tính giá trị của biểu thức
12
21
3
xx
Axx
=+−
Bài 3:(0.75 điểm) Gieo một con xúc sắc cân đối và đồng chất 24 lần. Số chấm xuất hiện được ghi
lại trong bảng sau:
1
3
2
4
1
4
5
4
5
1
5
2
4
6
1
3
6
4
2
3
1
2
4
5
a) Lập bảng tần số cho mẫu số liệu trên
b) Vẽ biểu đồ đoạn thẳng biểu diễn số liệu ở bảng tần số
Bài 4:(0.75 điểm) Một ô tô khách và một ô tô tải chở vật liệu xây dựng khởi hành cùng một lúc
từ bến xe khách Lai Châu đến trung tâm thị trấn Mường Tè. Do trọng tải lớn nên xe tải chở vật
liệu xây dựng đi với vận tốc chậm hơn xe khách
Xe khách đến trung tâm thị trấn
Mường Tè sớm hơn xe tải 1 giờ 6 phút. Biết quãng đường từ bến xe khách thành phố Lai Châu
đến trung tâm thị trấn Mường Tè là
132 km.
Tính vận tốc của xe tải.
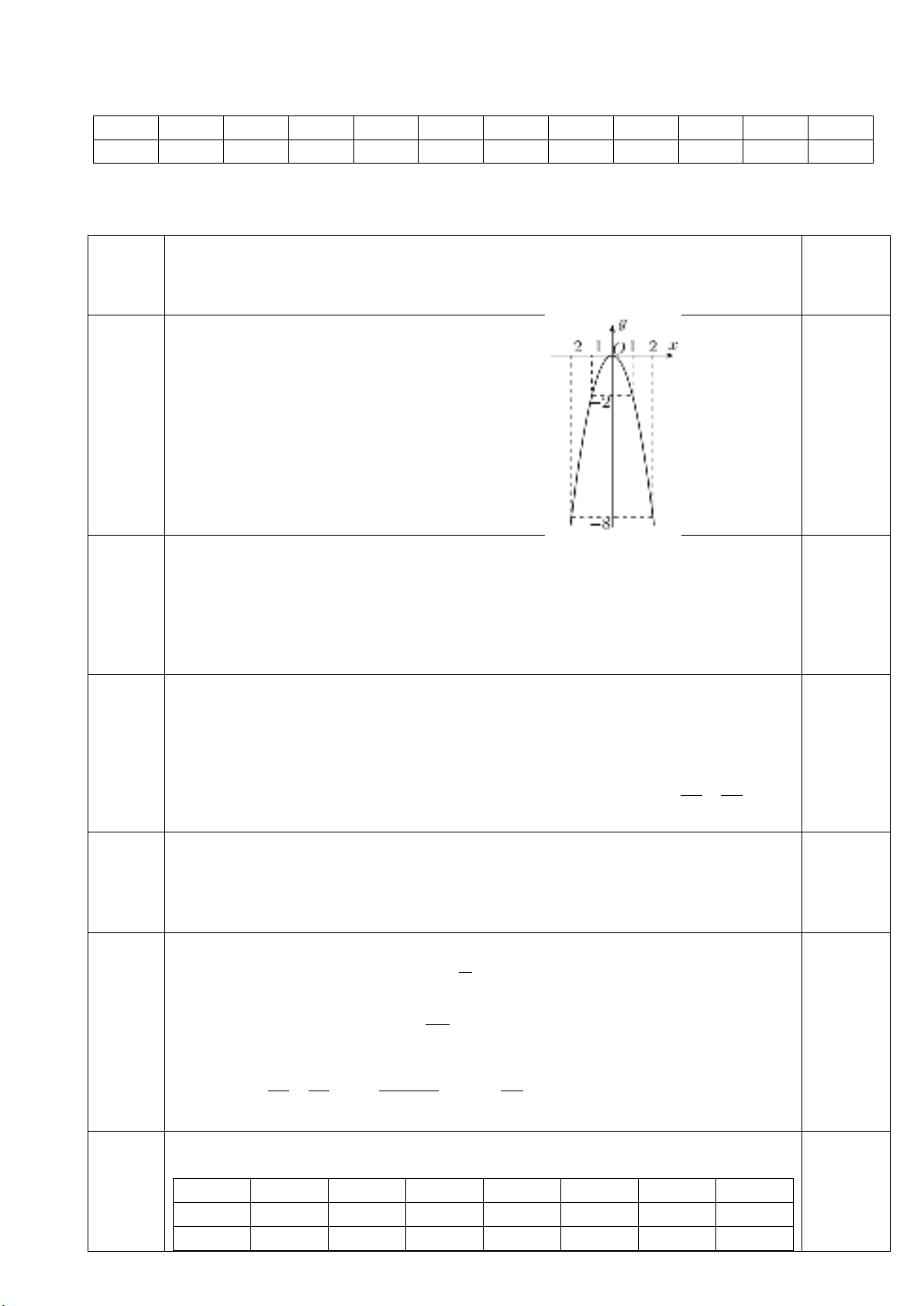
Bài 5:(1.0 điểm) Một khối đồ chơi gồm hai khối trụ
( )
1
H
,
( )
2
H
xếp chồng
lên nhau, lần lượt có bán kính đáy và chiều cao tương ứng là
1
r
,
1
h
,
2
r
,
2
h
thỏa mãn
21
1
2
rr=
,
21
2hh=
(tham khảo hình vẽ). Biết rằng thể tích của toàn
bộ khối đồ chơi bằng
3
30 cm .
Biết
2.
tru
V Rh
π
=
a) Chứng minh thể tích khối trụ (H2) bằng nửa thể tích khối trụ (H1).
b) Tính thể tích khối trụ (H1).
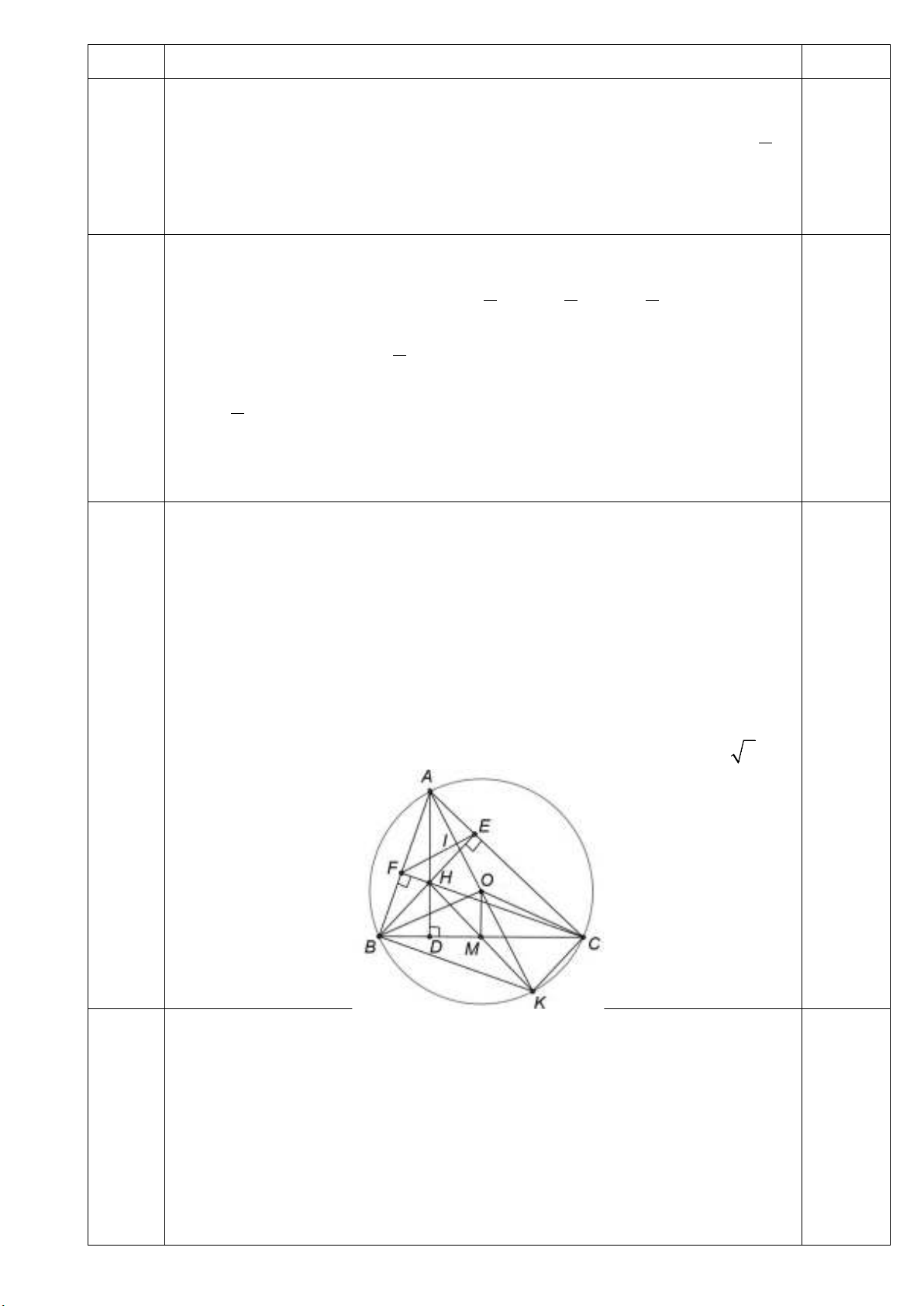
Bài 6:(2.5 điểm) Cho tam giác
ABC
nhọn có
AB AC<
nội tiếp đường tròn
( )
;OR
. Các đường
cao
;BE CF
của tam giác cắt nhau tại
H
(
E
thuộc
,AC F
thuộc
)
.AB
a) Chứng minh: Tứ giác
BFEC
nội tiếp đường tròn.
b) Kẻ đường kính
AK
của đường tròn
( )
O
. Chứng minh
AK
vuông góc với
EF
.
c) Giả sử
BC
cố định và
A
di chuyển trên cung lớn
BC
sao cho tam giác
ABC
luôn là tam
giác nhọn. Xác định vị trí của điểm
A
để diện tích tam giác
EAH
lớn nhất. Tính giá trị lớn nhất
đó theo
R
khi
3.BC R=
HẾT
(H2 )
(H1)
ĐÁP ÁN VÀ THANG ĐIỂM
PHẦN TRẮC NGHIỆM (3,0 ĐIỂM)
1
2
3
4
5
6
7
8
9
10
11
12
B
A
D
A
A
C
B
D
A
A
D
C
PHẦN TỰ LUẬN (7,0 ĐIỂM)
Bài 1
Cho hàm số
2
2yx= −
có đồ thị là (P)
a) Vẽ (P) trên mặt phẳng tọa độ Oxy
b) Tìm tọa độ những điểm M thuộc (P) có tung độ bằng - 8
1.0
a)
- Lập bảng giá trị đúng
- Vẽ đồ thị hàm số đúng
0.25
0.25
b)
Thay y = -8 vào hàm số
2
2yx= −
ta có:
2
2
82
4
x
x
−=−
=
x = 2 hoặc x =-2
Vậy M(2;-8) và M(-2; -8)
0.25
0.25
Bài 2
Cho phương trình:
2
2 5 40xx− −=
a) Chứng minh phương trình có 2 nghiệm phân biệt
12
,xx
b) Không giải phương trình, tính giá trị của biểu thức
12
21
3
xx
Axx
=+−
1.0
a)
Ta có:
2
4 57 0b ac∆= − = >
nên phương trình có hai nghiệm phân biệt
12
,xx
0.5
b)
Theo định lý Vi – ét:
12
12
5
2
4
.2
2
xx
xx
+=
−
= = −
Ta có:
22
1 2 12
2 1 12
65
33
.8
xx xx
Ax x xx
+
= + −= −=−
0.5
Bài 3
Gieo một con xúc sắc cân đối và đồng chất 24 lần. Số chấm xuất hiện được
ghi lại trong bảng sau:
1
3
2
4
1
4
5
4
5
1
5
2
4
6
1
3
6
4
2
3
1
2
4
5
0.75
a) Lập bảng tần số cho mẫu số liệu trên
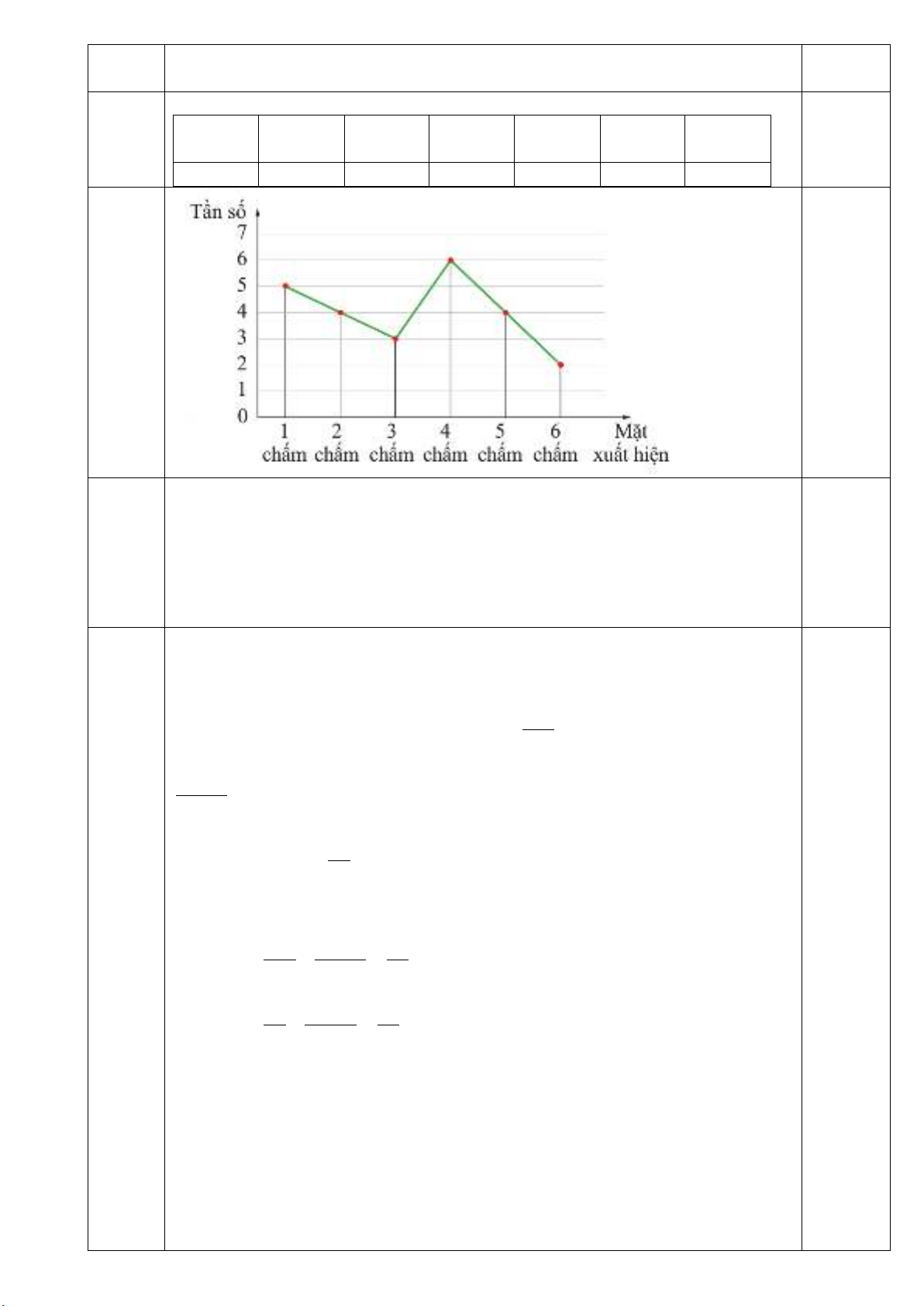
b) Vẽ biểu đồ đoạn thẳng biểu diễn số liệu ở bảng tần số
a)
Bảng tấn số:
Số
chấm
1
2
3
4
5
6
Tần số
5
4
3
6
4
2
b)
Bài 4
Một ô tô khách và một ô tô tải chở vật liệu xây dựng khởi hành cùng một
lúc từ bến xe khách Lai Châu đến trung tâm thị trấn Mường Tè. Do trọng tải
lớn nên xe tải chở vật liệu xây dựng đi với vận tốc chậm hơn xe khách
Xe khách đến trung tâm thị trấn Mường Tè sớm hơn xe tải 1 giờ
6 phút. Biết quãng đường từ bến xe khách thành phố Lai Châu đến trung
tâm thị trấn Mường Tè là
132 km.
Tính vận tốc của xe tải.
0.75
Gọi x(km/h) là vận tốc xe tải ( x > 0)
Khi đó, vận tốc của xe khách là
10 (km/h).x+
Thời gian đi hết quãng đường của xe tải là
132
x
(giờ) và của xe khách là
132
10x+
(giờ).
Đổi 1 giờ 6 phút
11
10
=
giờ.
Vì xe khách đi nhanh hơn xe tải 1 giờ 6 phút nên ta có phương trình:
132 132 11
10 10xx
−=
+
12 12 1
10 10xx
−=
+
( ) ( )
120 10 120 10x x xx+− = +
2
120 1200 120 10x xx x+−=+
2
10 1200 0xx+− =
30x=
(TMĐK) hoặc
40x= −
(loại).
Vậy vận tốc xe tải là 30 km/h
0.25
0.25
0.25
Bài 5
Một khối đồ chơi gồm hai khối trụ
( )
1
H
,
( )
2
H
xếp chồng lên nhau, lần lượt
có bán kính đáy và chiều cao tương ứng là
1
r
,
1
h
,
2
r
,
2
h
thỏa mãn
21
1
2
rr=
,
21
2hh=
(tham khảo hình vẽ). Biết rằng thể tích của toàn bộ khối đồ chơi bằng
3
30 cm .
Tính thể tích khối trụ
( )
1
H
. Biết
2
.
tru
V Rh
π
=
1.0
Thể tích khối
( )
1
H
là
2
1 11
V rh
π
=
.
Thể tích khối
( )
2
H
là
22 2
2 22 1 1 11 1
111
2
422
V rh r h rh V
ππ π
= = = =
.
Mà
12
30VV+=
nên
11
130
2
VV+=
.
Do đó
1
330
2V=
hay
3
1
20 cm .V=
Vậy thể tích của khối
( )
1
H là
3
20 cm .
0. 5
0.25
0.25
Bài 6
Cho tam giác
ABC
nhọn có
AB AC<
nội tiếp đường tròn
( )
;OR
. Các
đường cao
;BE CF
của tam giác cắt nhau tại
H
(
E
thuộc
,AC F
thuộc
)
.AB
a) Chứng minh: Tứ giác
BFEC
nội tiếp đường tròn.
b) Kẻ đường kính
AK
của đường tròn
( )
O
. Chứng minh
AK
vuông góc
với
EF
.
c) Giả sử
BC
cố định và
A
di chuyển trên cung lớn
BC
sao cho tam
giác
ABC
luôn là tam giác nhọn. Xác định vị trí của điểm
A
để diện tích
tam giác
EAH
lớn nhất. Tính giá trị lớn nhất đó theo
R
khi
3.BC R=
2.5
a)
Ta có
,BE CF
là hai đường cao của tam giác
ABC
nên
90 .BFC BEC= = °
Tam giác
BCE
vuông tại
E
nên
,,BCE
thuộc đường tròn đường kính
.BC
Tam giác
BFC
vuông tại
F
nên
,,BCF
thuộc đường tròn đường kính
.BC
Do đó
,,,BCEF
thuộc đường tròn đường kính
.BC
Hay tứ giác
BFEC
là tứ giác nội tiếp.
1.0