1
SỞ GIÁO DỤC & ĐÀO TẠO
THANH HÓA
TRƯỜNG THPT BÁ THƯỚC
ĐỀ THI GIAO LƯU HỌC SINH GIỎI CẤP TỈNH
NĂM HỌC 2019 - 2020
Môn thi: Toán - Lớp 11
Thời gian làm bài: 180 phút (không kể thời gian giao đề )
Ngày thi: 28 tháng 12 năm 2019
(Đề thi có 01 trang, gồm 05 câu)
Câu I (4.0 điểm).
1. Lập bảng biến thiên và vẽ đồ thị
( )
P
của hàm số
23y ax bx= +−
, biết rằng
( )
P
có
đỉnh
( )
2;1I
.
2. Giải bất phương trình:
( ) ( )
2
1 2 6 7 7 12 .x x x x xx+ ++ + +≥ + +
Câu II (4.0 điểm).
1. Giải phương trình:
( )
2
2 3sin . 1 cos 4cos .sin 3
20.
2sin 1
x
xxx
x
+− −
=
−
2. Giải hệ phương trình:
( ) ( ) ( )
22
6 1 2 4 2 2 10 ;
2 13 1 1
yx y x x xy
x x xy xy y
− − ++ + +=
∈
++ +− −= + −+ −
.
Câu III (4.0 điểm).
1. Cho
là các số thực dương thay đổi thỏa mãn điều kiện
xyz x z y++=
. Tìm giá trị
lớn nhất của biểu thức:
22 2 22
224 3
11 1 ( 1) 1
zz
Pxy z zz
=−− +
++ + ++
.
2. Cho dãy số
( )
n
u
thỏa mãn điều kiện
12u=
và
2
123
... , 1,2,...
nn
u u u u nu n+ + + + = ∀=
Tìm công thức số hạng tổng quát
n
u
của dãy số
( )
n
u
.
Câu IV (4.0 điểm).
1. Một hộp đựng
50
chiếc thẻ được đánh số từ
1
đến
50
. Chọn ngẫu nhiên từ hộp hai thẻ.
Tính xác suất để hiệu bình phương số ghi trên hai thẻ là số chia hết cho
3
.
2. Trong mặt phẳng với hệ tọa độ
Oxy
, cho tam giác
ABC
cân tại
A
,
M
là trung điểm
của
AB
. Đường thẳng
: 2 70CM x y− +=
và
47
;
32
K


là trọng tâm tam giác
ACM
. Đường
thẳng
AB
đi qua điểm
( )
3; 1D−
. Tìm tọa độ các đỉnh của tam giác
ABC
, biết điểm
M
có hoành
độ nguyên và tâm đường tròn ngoại tiếp tam giác
ABC
thuộc đường thẳng
6 26 0.xy+−=
Câu V (4.0 điểm).
1. Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
3a
,
3SA SD a= =
,
33SB SC a= =
.
Gọi
M
,
N
lần lượt là trung điểm của các cạnh
SA
và
SD
,
P
là điểm thuộc cạnh
AB
sao cho
2AP a=
. Tính diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng
( )
MNP
.
2. Cho tứ diện
ABCD
,
G
là trọng tâm tam giác
BCD
và
M
là điểm di động bên trong
tam giác
BCD
sao cho khi
M
khác
G
thì
MG
không song song với
CD
. Đường thẳng qua
M
và song song với
GA
cắt các mặt phẳng
( )
ABC
,
( )
ACD
,
( )
ABD
lần lượt tại
,,PQR
. Tìm
giá trị lớn nhất của tích
..MP MQ MR
.
-------------------- Hết --------------------
2
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
Câu Ý
Nội dung
Điể
m
I
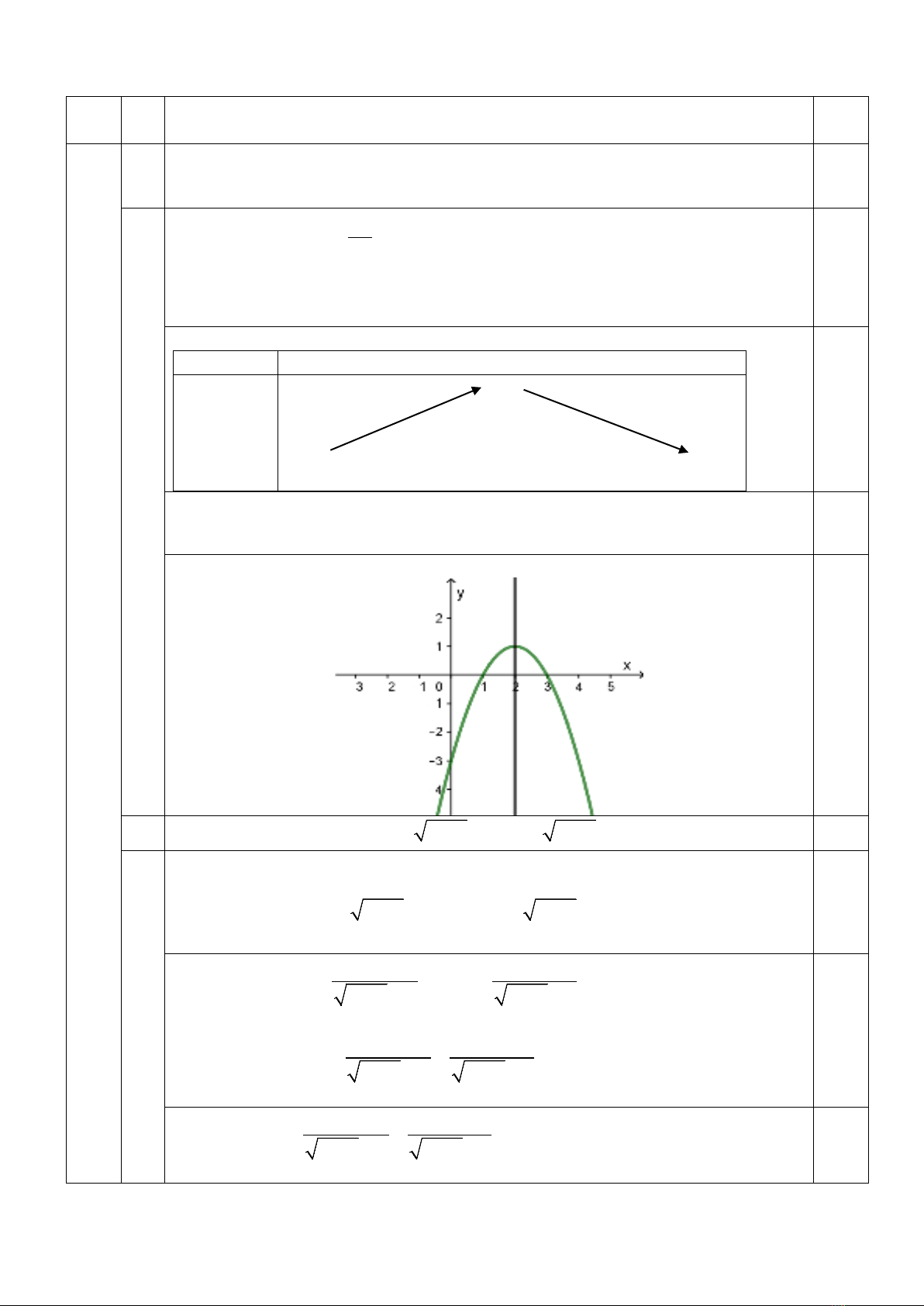
1 Lập bảng biến thiên và vẽ đồ thị
( )
P
của hàm số
23y ax bx= +−
, biết rằng
( )
P
có đỉnh
( )
2;1I
. 2,0
Từ giả thiết ta có:
40 1
2
2424 4
4 2 31
bab a
aab b
ab
+= =−
−= 
⇔⇔

+= =

+ −=
Vậy
( )
P
:
243yx x=−+ −
0,5
Bảng biến thiên:
x
−∞
2
+∞
y
−∞
1
−∞
0,5
Đồ thị hàm số có đỉnh
( )
2;1I
, trục đối xứng
2x=
Đồ thị hàm số cắt trục tung tại
( )
0; 3−
và cắt trục hoành tại
( ) ( )
1;0 , 3;0
0,5
Đồ thị hàm số như hình vẽ
0,5
2 Giải bất phương trình:
( ) ( )
2
1 2 6 7 7 12 .x x x x xx+ ++ + +≥ + +
2,0
Đk:
2.x≥−
BPT
( )
( )
( )
( )
2
1 22 6 73 2 8x x x x xx⇔ + +− + + +− ≥ + −
0,5
( ) ( ) ( )( )
22
1 6 24
22 73
xx
x x xx
xx
−−
⇔+ ++ ≥− +
++ ++
( ) ( )
16
2 40
22 73
xx
xx
xx
++

⇔− + −+ ≥

++ ++

0,5
Ta có
( )
16
4
22 73
xx
x
xx
++
+ −+
++ ++
0,5
3
=
2 2 6 61
22
22 73 22
xxxx
xxx
++++
−+ −−
++ ++ ++
=
( ) ( )
( )
6 71
22 10, 2
22 73 22
xx
xx x
x xx
+ ++
++
− − − < ∀ ≥−
++ ++ ++
BPT
20 2xx⇔−≤⇔≤
Vậy tập nghiệm của bất phương trình là
[ ]
2;2S= −
0,5
II
1 Giải phương trình:
( )
2
2 3sin . 1 cos 4cos .sin 3
20.
2sin 1
x
xxx
x
+− −
=
−
2,0
ĐK: Điều kiện:
2
16
sin ,
5
22
6
xk
xk
xk
ππ
ππ
≠+
≠⇔ ∈
≠+
(*). 0,25
Với điều kiện trên, phương trình đã cho tương đương:
( )
2
2 3 sin . 1 cos 4cos .sin 3 0
2
x
xxx+ − −=
( )
2 3 sin 2 3 sin .cos 2cos 1 cos 3 0x xx x x⇔ + − − −=
( ) ( )
22
2 3 sin cos 3sin 2 3 sin .cos cos 0x x x xx x⇔ −− − + =
0,5
( )( )
3 sin cos 0
3 sin cos 3 sin cos 2 0 3 sin cos 2
xx
xx xx
xx
−=
⇔ − − −=⇔
−=
0,25
TH1:
3 sin cos 0 cot 3 ,
6
x x x x kk
ππ
− =⇔ = ⇔= + ∈
0,25
TH2:
3sin cos 2 2 sin cos cos sin 2 sin 1
66 6
xx x x x
ππ π

− =⇔ − =⇔ −=


2
2 2,
62 3
x k x kk
ππ π
ππ
⇔− = + ⇔= + ∈
0,25
Đối chiếu điều kiện ta thấy phương trình đã cho có nghiệm
72
2, 2,
63
xkxkk
ππ
ππ
=+=+∈
0,5
2
Giải hệ phương trình:
( ) ( ) ( )
( ) ( )
22
6 1 2 4 2 2 10 1
;
2 1 3 1 12
yx y x x
xy
x x xy xy y
− − ++ + +=
∈
++ +− −= + −+ −
2,0
4
Điều kiện:
2
1
2
1
10
10
x
y
x xy
xy
≥−
≥
+ − −≥
+ −≥
( ) ( ) ( ) ( )
( ) ( ) ( )
2 63 2221210
2 2321 2221210
1y x y xx
y y xy
Pt
xx

⇔ + − + ++ + +=

⇔ + +− + ++ + +=
0,5
Đặt
( )
2; 2 1; 0; 0ayb x ab=+= + >≥
ta được:
( ) ( )
2
3 23
3 20 20a ab b a b a b a b− + =⇔ − + =⇔=
( )
2 21 21 211 1y x yx x x⇒ + = +⇔ = − ⇒ −≥⇔ ≥
0,5
Thay
21yx= −
vào (2) ta được:
( )
()
( )
( )
( )
22
22
2
2
2
2 33 2 2 2
32 223 320
13
3 21 0
32
22
1
3 20 /
2
x xx x x
x x xx x x x
xx xx
xx x
x
x x tm
x
++ − = −+ −
⇔ − + + −− − + − − =

⇔ −+ + + =

+−
−+ −

=
⇔ − +=⇔
=
0,5
( )
( ) ( )
{ }
;
11
23
: 1;1 , 2; 3
xy
xy
xy
KL T
+=⇒ =
+=⇒ =
=
0,5
III
1
Cho
,,xyz
là các số thực dương thay đổi thỏa mãn điều kiện
xyz x z y++=
.
Tìm giá trị lớn nhất của biểu thức:
22 2 22
224 3
11 1 ( 1) 1
zz
Pxy z zz
=−− +
++ + ++
. 2,0
Đặt
tan , tan , tan , (0 , , )
2
x Ay Bz C ABC
π
= = = <<
Theo giả thiết ta có:
tan tan
tan tan( )
1 1 tan tan
yz B C
x A BC A BCk
yz B C
π
−−
= ⇔ = = − ⇒=−+
++
Do
0
2ABC k AB C
ππ
−<−+<⇒=⇒−=−
. Khi đó:
0,5
22 2 22
22 2 2
1 1 4 tan 3tan
2( )
1 tan 1 tan 1 tan (1 tan ) 1 tan
2( os os ) 4sin 3sin .cos cos 2 os2B 4sin 3sin .cos
CC
PAB C CC
c Ac B C C C Ac C C C
= −− +
++ + ++
= −−+ =−−+
( ) ( )
2
2sin sin 4sin 3sin .cosAB AB C C C=− − +− + =
( )
2
2sin .sin 4sin 3sin .cosC AB C C C= +− + =
22 2
2sin 4sin 3sin .cos sin (3cos 2) sin (1 3sin )C C CC C C C C≤ − + = −= −
0,5
Nếu
3
sin 0
3
CP> ⇒<
. 0,5
5
Nếu
3
sin 3
C≤
. Áp dụng bất đẳng thức Côsi cho 3 số không âm
22 2
2 2 22
6sin (1 3sin )(1 3sin )
sin (1 3sin ) 6
CC C
PC C −−
=−=
222
3
1 6sin 1 3sin 1 3sin 4
()
6 3 81
CCC+− +−
≤=
2
9
P⇒≤
.
Dấu ‘’ = ‘’ xảy ra khi
12
sin tan
3422
sin( ) 1 tan cot tan , tanA= , tan 2
42
tan tan 2
1 tan tan 4
CC
AB B A C B
AB C AB
AB
==
+=⇒ = ⇒ = =


−=− −

= −
+
22
2; ;
24
xy z⇒= = =
.Vậy giá trị lớn nhất của P bằng
2
9
.
0,5
2
Cho dãy số
( )
n
u
thỏa mãn điều kiện
12u=
và
2
123
... , 1,2,...
nn
u u u u nu n+ + + + = ∀=
Tìm công thức số hạng tổng quát
n
u
của dãy số
( )
n
u
.
2,0
Với
2,n
ta có

12 2 2
2
4.
3
uu u u
Với mọi
2, 3,...,n
ta có

2
12 1
... ,
nn n
u u u u nu


2
12 1 1
... 1 .
nn
uu u n u
0,5
Trừ hai đẳng thức trên ta được

2
2
1
1 ,3
nn n
u nu n u n

2
2
1
1 1 ,3
nn
nunun

1
1,3
1
nn
n
u un
n
0,5



2
2
6
1 2 32 4
. ... . , 3.
1 54 11
n
u
nn
uu n
nn nn nn
0,5
Với
1, 2nn= =
công thức trên vẫn đúng.
Vậy
( )
*
4,
1
n
un
nn
= ∀∈
+
. 0,5
IV
1
Một hộp đựng 50 chiếc thẻ được đánh số từ 1 đến 50. Chọn ngẫu nhiên từ
hộp hai thẻ. Tính xác suất để hiệu bình phương số ghi trên hai thẻ là số
chia hết cho 3.
2,0
( )
2
50
nCΩ=
Gọi A là biến cố hiệu bình phương số ghi trên hai thẻ là số chia hết cho 3
Giả sử 2 số được chọn là
a,b
. Theo giả thiết
( )
( )( ) ( )
( )
22 3
33
3
ab
a b abab ab
−
− ⇔− + ⇔
+

0,5
Nếu
( )
3ab−
thì a, b phải đồng dư khi chia 3
⇒
số cách chọn là:
222
16 17 17
CCC++
Nếu
( )
3ab+
thì hoặc a và b cùng chia hết cho 3 hoặc một số chia 3 dư 1,
0,5