
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
THỊ XÃ VĨNH CHÂU
¯¯¯¯¯¯¯¯¯
KÌ THI CHỌN HỌC SINH GIỎI CẤP THỊ XÃ
Năm học 2023-2024
Môn: Tin học 9
Thời gian 150 phút không kể thời gian giao đề
(Đề thi có 02 trang)
Trên ổ đĩa D, Thí sinh làm và lưu tên theo dạng sau: «SBD_Bai», ví dụ: 05_Bai1»
Thí sinh có thể dùng ngôn ngữ lập trình phù hợp: Pascal, Scracth, …
Bài 1 (10.0 điểm): Thí sinh chọn 1 trong 2 câu sau đây
Câu 1. Viết chương trình cho phép nhập từ bàn phím một số nguyên dương a
và thực hiện:
a. Cho biết a là số có mấy chữ số.
b. Cho biết tổng các chữ số của a.
c. Ta gọi số “đối xứng” với a là số nguyên dương thu được từ a bằng cách đảo
ngược thứ tự các chữ số của a. Viết chương trình in ra số đối xứng của số nguyên
dương a.
d. Cho a và b là 2 số nguyên dương. Ta gọi tổng đối xứng của a và b là số đối
xứng với tổng của số đối xứng với a và số đối xứng với b. Viết chương trình cho
phép nhập hai số nguyên dương a, b và in ra tổng đối xứng của chúng.
Ví dụ: Nhập a = 25 thì cho kết quả là:
a. So a co 2 chu so.
b. Tong cac chu so cua a la 7.
c. So doi xung cua a la 52.
d. Nếu a = 25 và b = 26 thì tổng của số đối xứng với a và số đối xứng với b là
52 + 62 = 114. Vì thế tổng đối xứng của a và b là 411.
Câu 2. Dãy số
Nhập vào bàn phím số nguyên dương n (2 < N < 20) và N số nguyên A[1]
….A[N] có giá trị tuyệt đối không vượt quá 1000.
Xuất ra màn hình các kết quả sau đây:
+ Dòng 1: In ra N số nguyên B[1]….B[N], trong đó B[i] là số lớn nhất trong
các số A[1]….A[N], với 1< i < N.
+ Dòng 2: In ra giá trị S nhỏ nhất trong tất cả các giá trị tuyệt đối cuYa tổng hai
số hạng bất kỳ của dãy đã cho.
+ Dòng 3: In ra giá trị T lớn nhất trong tất cả cá giá trị tuyệt đối của tổng một
số số hạng nào đó của dãy đã cho.
Ví dụ: Với N = 5 và 5 là số nguyên 1, -7, 3, 1,7 ta có kết quả 5 số nguyên 1, 1,
3, 3, 7 và S = 0 còn T = N.
1 | 2
Bài 2 (10.0 điểm): Số đối xứng
Số đối xứng là số có thể viết từ trái sang phải hay viết từ phải sang trái các chữ
số của nó ta vẫn được chính nó, ví dụ các số 363, 1221, 474 là số đối xứng. Có một
số x ta lấy các chữ số từ phải qua trái của nó viết lại theo thứ tự từ trái qua phải ta
thu được một số mới k, số k gọi là số đảo của số x. Ví dụ x=123 thì k=321; x=130
thì k=031 (giá trị thực của k=31 vì số 0 đầu không có nghĩa).
Cho một số nguyên dương n, qua phép biến đổi sau đây ta luôn thu được một
số đối xứng: Lấy số n cộng với số đảo của nó thu được tổng là n1, nếu n1 chưa là số
đối xứng thì tiếp tục lấy n1 cộng với số đảo của n1 thu được tổng n2 và tiếp tục làm
như vậy đến khi nhận được số đối xứng.
Ví dụ, từ số 48 ta có 48+84 = 132, 132+231 = 363. Như vậy 48 tương ứng với 363.
Yêu cầu: Viết chương trình nhập số nguyên dương n ( 10< N ≤ 65000). Xuất
ra màn hình số đối xứng thu được qua phép biến đổi trên và số lần biến đổi để thu
được số đối xứng.
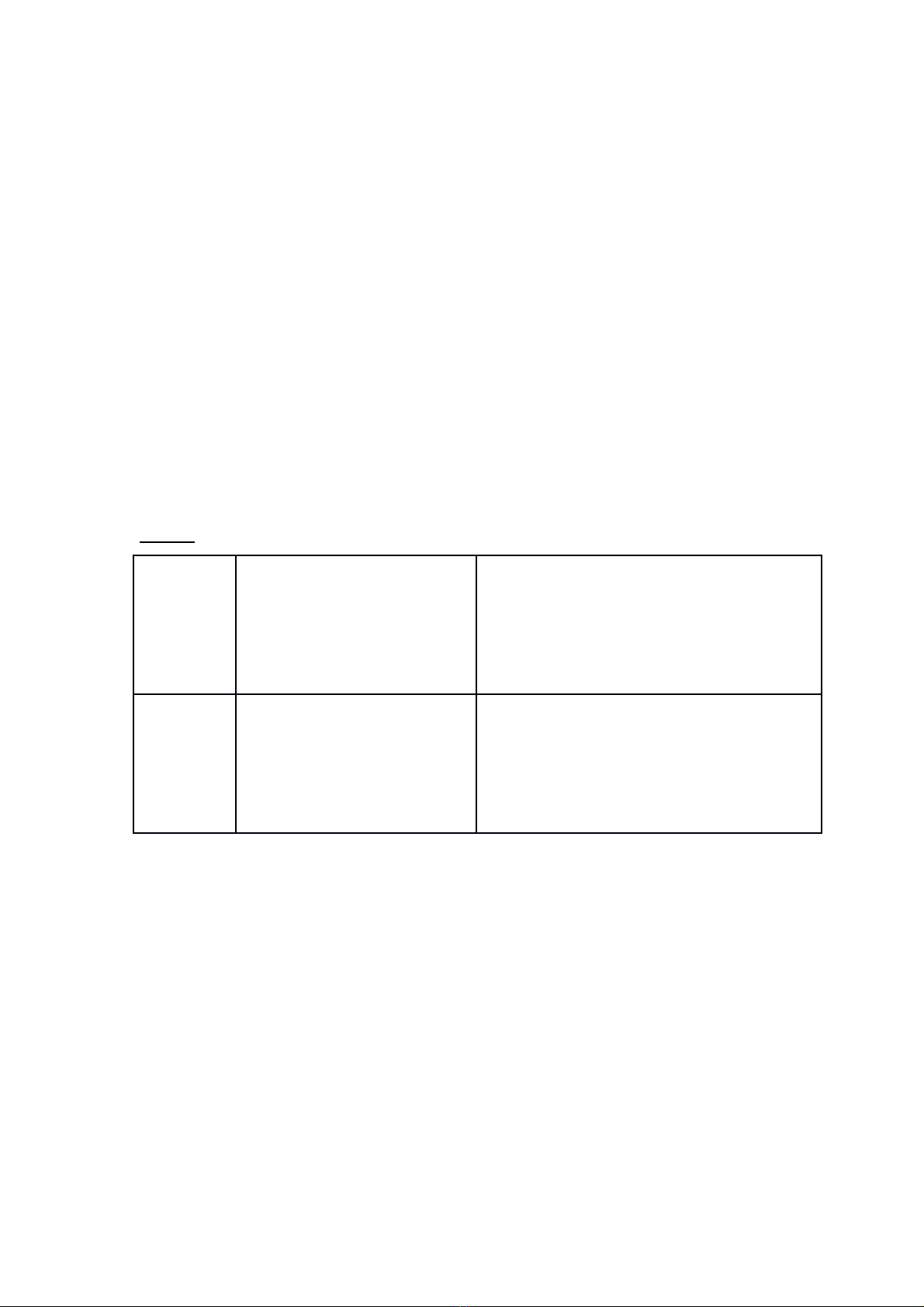
Ví dụ:
Nhập n Kết quả trên màn hình Giải thích
157
So doi xung = 8888
So lan bien doi = 3
157+751=908 (biến đổi lần 1)
908+809=1717 (biến đổi lần 2)
1717+7171=8888 (biến đổi lần 3 thu
được số đối xứng)
--------- Hết ---------
(Cán bộ coi thi không giải thích gì thêm)
2


![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)




![Đề thi học kì 2 Vật lý lớp 11: Đề minh họa [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250709/linhnhil/135x160/711752026408.jpg)








