UBND HUYỆN THANH TRÌ
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC SINH NĂNG KHIẾU
NĂM HỌC: 2020 – 2021
Môn: TOÁN 8
Thời gian làm bài:120 phút
Bài 1: (4,0 điểm)
1. Phân tích đa thức sau thành nhân tử:
22
2 445− ++−−x xy y x y
2. Phân tích đa thức thành nhân tử:
4 4 22 2 2
2− − ++x y xy x y
Bài 2: (4,0 điểm)
1. Cho
a
là số nguyên tố lớn hơn 3. Chứng minh rằng
21 24−a
2. Tìm tất cả các số nguyên dương
n
để số
11...1 77...7= −a
là bình phương đúng(với
2n
chữ số
1
,
chữ số
7
).
Bài 3:(3,0 điểm)
1. Giải phương trình:
( )( )
2 42
4 11 8 21 35−+ − + =xx xx
2. Cho các số thực
,,xyz
thỏa mãn đồng thời các điều kiện:
2,++=xyz
2 22
18++=xyz
và
1.= −xyz
Tính giá trị của
111
111
=++
+− +− +−
Sxy z yz x xz y
Bài 4:(2,0 điểm)
Cho
,,abc
là độ dài ba cạnh của tam giác thỏa mãn
1.++=abc
Chứng minh:
222
1.
2
++<abc
Bài 5:(6,0 điểm)
Cho
O
là trung điểm của đoạn thẳng
AB
có độ dài bằng
2a
. Trên cùng một nửa mặt phẳng bờ
là
AB
, vẽ hai tia
Ax
và
By
cùng vuông góc với
AB
. Trên tia
Ax
lấy điểm
D
bất kì (
D
khác
A
). Qua
O
kẻ đường vuông góc với
OD
tại
O
, cắt
By
tại
C
. Gọi
H
là hình chiếu vuông góc của
O
trên
.CD
1. Chứng minh:
..=
AD OC OB OD
2.Chứng minh:
∆∆ADH BOH∽
và
∆AHB
vuông.
3. Gọi
I
là giao điểm của
AC
và
BD
,
E
là giao điểm của
AH
và
DO
,
F
là giao điểm của
BH
và
.CO
Chứng minh:
,,EIF
thẳng hàng.
4.Tìm vị trí của
D
trên
Ax
để diện tích tứ giác
ABCD
nhỏ nhất? Tìm giá trị nhỏ nhất đó?
Bài 6: (1,0 điểm)
Tìm
,
y
,
z
nguyên dương thỏa mãn:
( ) ( )
23
3
34− ++ = + +x xyz yz
.
= = = = = = = = = = HẾT = = = = = = = = = =
(Học sinh không được sử dụng máy tính cầm tay)
ĐÁP ÁN ĐỀ KIỂM TRA HỌC SINH NĂNG KHIẾU
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO THANH TRÌ
Năm học: 2020-2021
HƯỚNG DẪN GIẢI CHI TIẾT
Bài 1: (4,0 điểm)
1. Phân tích đa thức sau thành nhân tử:
22
2 445− ++−−x xy y x y
2. Phân tích đa thức thành nhân tử:
4 4 22 2 2
2− − ++x y xy x y
Lời giải
1. Phân tích đa thức sau thành nhân tử:
22
2 445
− ++−−
x xy y x y
( )
22
2 4( ) 5= − + + −−x xy y x y
2
( ) 4( ) 4 9.

= − + −+−

xy xy
22
( 2) 3= −+ −xy
( 2 3)( 2 3)= −+− −++xy xy
( 1)( 5)
= −− −+
xy xy
2. Phân tích đa thức thành nhân tử:
4 4 22 2 2
2− − ++x y xy x y
( ) ( ) ( )
44 222 42
=−− −−−x y xy x y y
()( ) ( ) ( )
2 2 2 2 22 22
11= − + − −− −x y x y xy yy
( )( ) ( )( )
2222 2 22
1=+ −−− +xyxy y xy
( )( )
22222
1= + −−+
xyxyy
()( )
222 2
21
=+ −+xyx y
.
Bài 2: (4,0 điểm)
1. Cho
a
là số nguyên tố lớn hơn 3. Chứng minh rằng
2
1 24−a
2. Tìm tất cả các số nguyên dương
n
để số
11...1 77...7= −a
là bình phương đúng(với
2n
chữ số
1
,
n
chữ số
).
Lời giải
1. Ta có:
2
1 ( 1)( 1)−= + −a aa
+) Vì
a
là số nguyên tố lớn hơn 3 nên
a
là số lẻ
( 1)⇒−a
và
( 1)+a
là hai số chẵn liên tiếp.
( 1)( 1) 8⇒− +aa
+) Vì a là số nguyên tố lớn hơn 3 nên
a!3
suy ra
1−a
hoặc
1+a
chia hết cho 3
Do đó:
3( 1)( 1)
+−aa
Lại có: 3 và 8 nguyên tố cùng nhau nên
)( 1)( 1) (3.8+−aa
Hay:
21 24−a
với
a
là số nguyên tố lớn hơn 3.
2. Ta có :
11...1 77...7= −a
(với
2n
chữ số
1
,
n
chữ số
7
).
- Nếu
2
1 11 7 4 2
=⇒= −==na
là số chính phương.
- Nếu
1>n
111 111 777 77⇒= … − …a
.34
=…
, là số chia hết cho 2 nhưng không chia hết cho 4 nên
không là số chính phương.
Vậy
1=n
.
Bài 3:(3,0 điểm)
1. Giải phương trình:
( )( )
2 42
4 11 8 21 35−+ − + =xx xx
2. Cho các số thực
,,xyz
thỏa mãn đồng thời các điều kiện:
2,++=
xyz
2 22
18++=xyz
và
1.= −xyz
Tính giá trị của
111
111
=++
+− +− +−
Sxy z yz x xz y
Lời giải
1. Giải phương trình:
( )( )
2 42
4 11 8 21 35−+ − + =xx xx
.
Ta có:
( )( )
2 42
4 11 8 21−+ − +
xx xx
( )
2
22
( 2) 7 4 5 35 .


=−+ −+ ∀



xx x
Đẳng thức xảy ra khi:
( )
2
2
2
( 2) 0
40
−=
−=
x
x
20
( 2)( 2) 0
−=
⇔− +=
x
xx
2⇔=x
Do đó:
( )( )
2 42
4 11 8 21 35−+ − + =xx xx
2⇔=x
Vậy phương trình đã cho có tập nghiệm
{ }
2=S
.
2. Ta có:
( )
2 2 22 2
() 2
++ =+++ ++x y z x y z xy y xz
.
⇔
4 18 2( )=+ ++xy yz xz
⇔
7++=−xy yz xz
Vì
( )
22++=⇒=− +xyz z xy
Khi đó:
( ) ( )( )
1 2 1 1 11+−= +− + −= −− += − −xy z xy x y xy x y x y
11
1 ( 1)( 1)
⇒=
+− − −xy z x y
Tương tự :
11
1 ( 1)( 1)
=
+− − −yz x y z
;
11
1 ( 1)( 1)
=
+− − −zx y z x
111
111
⇒= + +
+− +− +−
Sxy z yz x xz y
( )( ) ( )( ) ( )( )
111
11 11 11
=++
−− −− −−xy yz zx
()( )( )
111
111
−+ −+ −
=−−−
zxy
xyz
( )
( )( )( )
3
111
++ −
=−−−
xyz
xyz
( ) ( )
23
1
−
=− + + + ++ −xyz xy yz zx x y z
1
1721
−
=−++−
1
7
−
=
.
Vậy
1
7
−
=S
.
Bài 4: (2,0 điểm)
Cho
,,abc
là độ dài ba cạnh của tam giác thỏa mãn
1.++=
abc
Chứng minh:
222
1.
2
++<abc
Lời giải
Vì
,,abc
là độ dài ba cạnh của tam giác
.⇒<+cab
2
()⇒< +c ca b
Tương tự:
2
()<+b ba c
2()<+a ab c
222
2( )⇒++< ++a b c ab bc ca
( )
1
Mà:
222 2
2( ) ( ) 1+ + + + + = ++ =a b c ab bc ca a b c
222
2( ) 1 ( )⇒ ++ =− ++ab bc ca a b c
( )
2
Từ
( )
1
và
( )
2
suy ra
( )
222 222
1++<− ++abc abc
Hay:
()
222
21++ <abc
222
1
2
++⇔<abc
(đpcm)
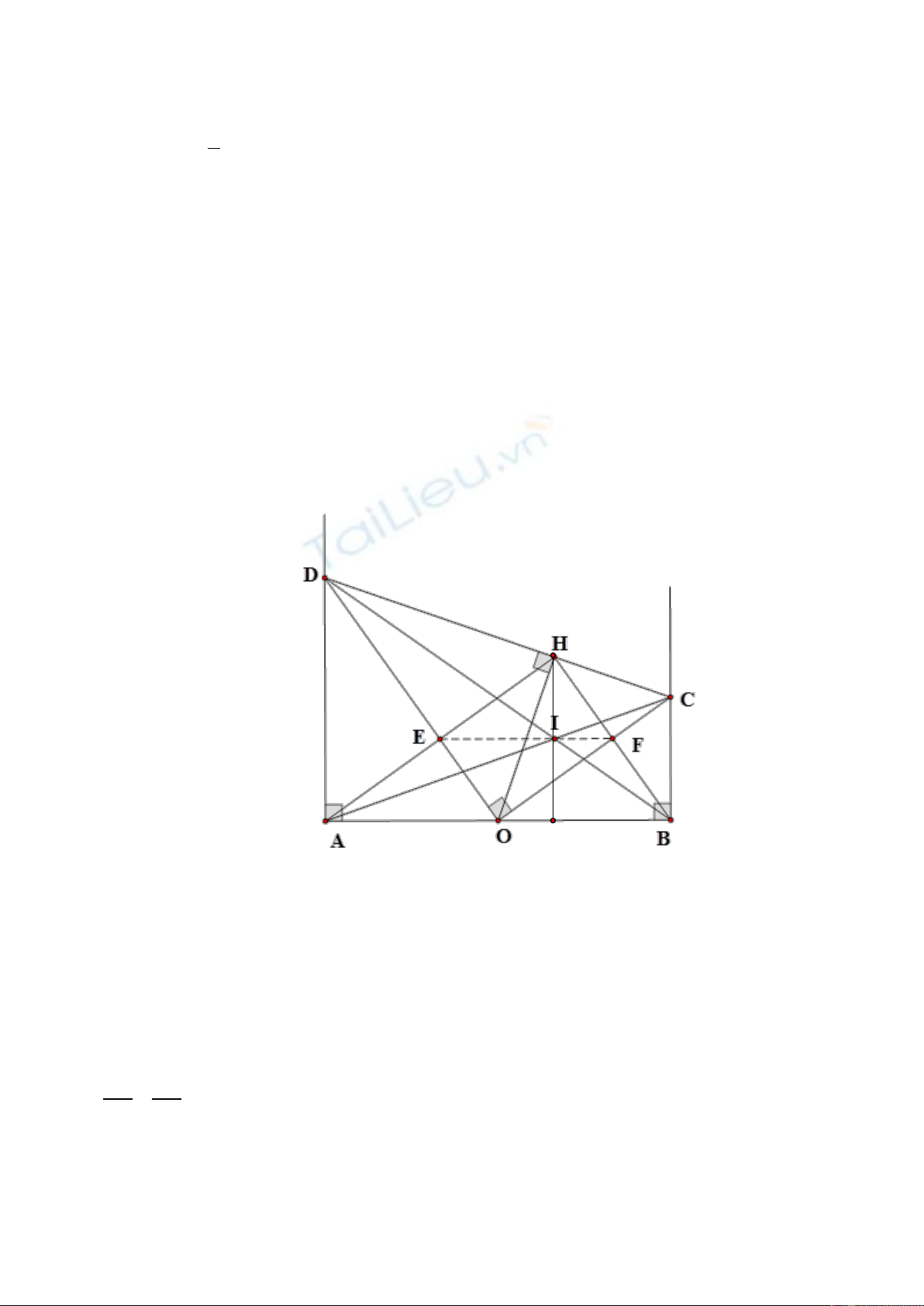
Bài 5: (6,0 điểm)
Cho
O
là trung điểm của đoạn thẳng
AB
có độ dài bằng
2a
. Trên cùng một nửa mặt phẳng bờ
là
AB
, vẽ hai tia
Ax
và
By
cùng vuông góc với
AB
. Trên tia
Ax
lấy điểm
D
bất kì (
D
khác
A
). Qua
O
kẻ đường vuông góc với
OD
tại
O
, cắt
By
tại
C
. Gọi
H
là hình chiếu vuông góc của
O
trên
.CD
1. Chứng minh:
..=AD OC OB OD
2. Chứng minh:
∆∆ADH BOH∽
và
∆AHB
vuông.
3. Gọi
I
là giao điểm của
AC
và
BD
,
E
là giao điểm của
AH
và
DO
,
F
là giao điểm của
BH
và
.CO
Chứng minh:
,,EIF
thẳng hàng.
4. Tìm vị trí của
D
trên
Ax
để diện tích tứ giác
ABCD
nhỏ nhất? Tìm giá trị nhỏ nhất đó?
Lời giải
a) Chứng minh:
..=AD OC OB OD
Xét
∆AOD
và
∆BCO
, ta có:
90= = °DAO CBO
=ADO COB
(cùng phụ với
AOD
)
⇒∆ ∆AOD BCO∽
(g.g)
⇒=
AD OD
BO OC
..⇒=AD OC OB OD
.
Vậy
..=AD OC OB OD
b) * Chứng minh:
∆∆ADH BOH∽
M
y
x