SỞ GD&ĐT VĨNH PHÚC KỲ THI CHỌN HSG LỚP 12 THPT NĂM HỌC 2019 - 2020
ĐỀ THI MÔN: TOÁN - THPT
ĐỀ CHÍNH THỨC Thời gian làm bài: 180 phút (không kể thời gian giao đề)
Câu 1. Cho hàm số 32
32 yx x mx có đồ thị là

.
m
C Tìm tất cả các giá trị thực của tham số
m để

m
C có điểm cực đại và điểm cực tiểu cách đều đường thẳng 1.yx
Câu 2. Tìm tất cả các giá trị thực của tham số m để hàm số cot 2
cot

x
y
x
m đồng biến trên khoảng
0; .
4



Câu 3. Giải phương trình: 31
8sin .
cos sin
x
x
x
Câu 4. Cho dãy số

n
u có số hạng tổng quát

2
ln 2
n
unn,

*.n Tính lim n
S biết
12
.
11 1
  

  
  
n
u
n
uu
See e
Câu 5. Giải phương trình: 2
43 12 125.  xxxxxx
Câu 6. Một hộp có 50 quả cầu được đánh số từ 1 đến 50. Lấy ngẫu nhiên 3 quả cầu từ hộp đó. Tính
xác suất để tích 3 số ghi trên 3 quả cầu lấy được là một số chia hết cho 8.
Câu 7. Cho hình lăng trụ ABC.A'B'C' có đáy là tam giác đều cạnh a, AA' = a. Hình chiếu vuông góc
của A' trên mặt phẳng (ABC) trùng với trung điểm cạnh AB. Gọi I là trung điểm của A'C, điểm S thỏa
mãn 2.
 
I
BSI Tính theo a thể tích khối chóp S.AA'B'B.
Câu 8. Cho tứ diện ABCD có G là trọng tâm tam giác BCD. Mặt phẳng (P) đi qua trung điểm I của
AG và cắt các đoạn AB, AC, AD tại các điểm khác A. Gọi A
h, B
h, C
h,
D
h lần lượt là khoảng cách từ
các điểm A, B, C, D đến mặt phẳng (P). Chứng minh rằng:
222
2.
3

BCD
A
hhh h
Câu 9. Trong mặt phẳng với hệ trục toạ độ Oxy, cho tam giác ABC vuông tại A. Điểm D là chân
đường phân giác trong góc A. Gọi M, N lần lượt là hình chiếu vuông góc của D trên AB, AC. Đường
tròn 22
():( 2) ( 1) 9Cx y ngoại tiếp tam giác DMN. Gọi H là giao điểm của BN và CM, đường
thẳng AH có phương trình 3100. xy Tìm tọa độ điểm B biết M có hoành độ dương, A có hoành
độ nguyên.
Câu 10. Cho a, b, c là các số thực dương thỏa mãn 1abc và 33
12.ab ba ab
ab Tìm giá trị
lớn nhất của biểu thức 22
113
.
1112


Pab c
---------- HẾT ----------
https://toanmath.com/
Thí sinh không được sử dụng tài liệu, máy tính cầm tay. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: ………………………………………………… Số báo danh: ……………….
SỞ GD&ĐT VĨNH PHÚC
KỲ THI CHỌN HSG LỚP 12 NĂM HỌC 2019-2020
ĐỀ THI MÔN: TOÁN - THPT
Thời gian: 180 phút, không kể thời gian giao đề
Câu 1. Cho hàm số 32
32yx x mx
có đồ thị là

m
C. Tìm tất cả các giá trị thực của tham
số m để

m
C có điểm cực đại và điểm cực tiểu cách đều đường thẳng 1
yx
.
Câu 2. Tìm tất cả các giá trị thực của tham số m để hàm số 2cotx
ycotx m

đồng biến trên
khoảng 0; .
4



Câu 3. Giải phương trình: 
31
8sinx cos
x
sin
x
.
Câu 4. Cho dãy số
n
u có số hạng tổng quát
2
ln 2 , * .
n
unnn Tính lim ,
n
S biết
12
11 1
... .
n
uu u
n
See e
  

  
  
Câu 5. Giải phương trình: 2
43 12 125xxxxxx   .
Câu 6. Một hộp có 50 quả cầu được đánh số từ 1 đến 50. Lẫy ngẫu nhiên 3 quả cầu từ hộp
đó. Tính xác suất để tích 3 số ghi trên 3 quả cầu lấy được là một số chia hết cho 8.
Câu 7. Cho hình lăng trụ .
A
BC ABC

có đáy là tam giác đều cạnh ,aAA a
. Hình chiếu
vuông góc của
A
trên mặt phẳng
A
BC trùng với trung điểm cạnh .AB Gọi
I
là trung điểm
của ,
A
C
điểm S thỏa mãn 2.IB SI
  Tính theo a thể tích khối chóp ..S AABB

Câu 8. Cho tứ diện ABCD có G là trọng tâm tam giác
B
CD . Mặt phẳng

P
đi qua trung
điểm
I
của AG và cắt các đoạn ,,
A
BACAD
tại các điểm khác A. Gọi ,,,
A
BCD
hhhh
lần lượt
là khoảng cách từ các điểm ,,,
A
BCD
đến mặt phẳng

P
. Chứng minh rằng:
222 2
3
BCD
A
hhh h

Câu 9. Trong mặt phẳng với hệ trục toạ độ ,Oxy cho tam giác ABC vuông tại A. Điểm D là
chân đường phân giác trong góc A. Gọi ,
M
N lần lượt là hình chiếu vuông góc của D trên
,
A
BAC
. Đường tròn

22
:( 2) ( 1) 9Cx y ngoại tiếp tam giác DMN . Gọi H là giao
điểm của
B
N và CM , đường thẳng AH có phương trình 3100
x
y . Tìm tọa độ điểm
B
biết
M
có hoành độ dương, A có hoành độ nguyên.
Câu 10. Cho ,,abc
là các số thực dương thỏa mãn 1abc và 33
12.ab ba ab
ab

Tìm giá
trị lớn nhất của biểu thức 22
113
1112
Pab c


.
---------------Hết----------------
Thí sinh không được sử dụng tài liệu, máy tính cầm tay. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:……….……..…….................…….….….; Số báo danh:……….....……….
ĐỀ CHÍNH TH
Ứ
C
SỞ GD&ĐT VĨNH PHÚC
KỲ THI CHỌN HSG LỚP 12 NĂM HỌC 2019-2020
HƯỚNG DẪN CHẤM MÔN: TOÁN - THPT
(Hướng dẫn chấm có 05 trang)
I. LƯU Ý CHUNG:
- Hướng dẫn chấm chỉ trình bày một cách giải bao gồm các ý bắt buộc phải có trong bài làm
của học sinh. Khi chấm nếu học sinh bỏ qua bước nào thì không cho điểm bước đó.
- Nếu học sinh làm theo cách khác, giám khảo căn cứ các ý trong hướng dẫn chấm để cho
điểm.
- Trong bài làm, nếu ở một bước nào đó bị sai thì các phần sau có sử dụng kết quả sai đó sẽ
không được điểm.
- Trong lời giải câu 7, 8 nếu học sinh không vẽ hình hoặc vẽ hình sai thì không cho điểm.
- Điểm toàn bài tính đến 0,5 và không làm tròn.
II. ĐÁP ÁN:
Câu Nội dung
1
Cho hàm số 32
32yx x mx có đồ thị là

m
C. Tìm tất cả các giá trị thực của tham
số m để

m
C có điểm cực đại và điểm cực tiểu cách đều đường thẳng 1
yx
.
Ta có: 2
'3 6
y
xxm.
Hàm số có cực trị '0y
có 2 nghiệm phân biệt 2
36 0xxm
có 2 nghiệm phân
biệt 12
;
x
x'93 0 3mm (*)
Thực hiện phép chia y cho 'y ta được: 11 2
'22
33 3 3
mm
yxy x




Ta có:
 
11 1 222
22
22; 22
33 33
 
 
 
 


yyx yy m
x
mm m
xx
Phương trình đường thẳng đi qua 2 điểm cực trị là 2
:22
33
mm
yx




Các điểm cực trị cách đều đường thẳng
yx
1
khi và chỉ khi
TH1: Đường thẳng đi qua 2 điểm cực trị song song hoặc trùng với đường thẳng
yx
1
29
21
32
mm



 (loại)
TH2: Trung điểm
I
của
A
B nằm trên đường thẳng
yx
1
 
212 1
12 2
1
11
2
2222 2
323
II
yy xx m m
xx xxxy
 




22.2 22 2 2 0
33
mm
m



 (thỏa mãn (*))
Vậy giá trị của m cần tìm là: 0m.
2
Tìm tất cả các giá trị thực của tham số m để hàm số 2cotx
ycotx m

đồng biến trên khoảng 0; .
4



Ta có


2
2
12
sin
cot
m
x
y
xm


Hàm số đã cho đồng biến trên khoảng 0; 4



hàm số đó xác định và 0, 0; 4
yx





1;
20
m
m


.
1m
. Vậy 1m thì hàm số đã cho đồng biến trên khoảng 0; 4



.
3
Giải phương trình: 
31
8sinx cos
x
sin
x
Điều kiện:

sin 0 sin 2 0 (*)
cos 0 2
xxxkk
x

Với điều kiện (*), phương trình đã cho 2
8sin cos 3sin cos
x
xxx
4 4cos 2 cos 3sin cos 4cos 4cos2 cos 3sin cos
3cos 2cos 2cos3 3sin cos 3sin 2cos3
x
xxxxxxxx
xx x xx x x


13
cos sin cos3 cos cos3
22 3
x
xx x x




32
36
32
312 2
xx k xk
xx k
x
k
 

 
(thỏa mãn (*) )
Vậy nghiệm của phương trình đã cho là:

;
6122
xkx kk

 .
4
Cho dãy số

n
u có số hạng tổng quát


2
ln 2 , * .
n
unnn Tính lim ,
n
S biết
12
11 1
... .
n
uu u
n
See e
  

  
  
Ta có


2
ln 2
11 1111
22 2
n
u
nn
ennnn
e





Suy ra 111111 11
1...
232435 2
n
Snn




11111311
1
22 1 222 1 2nn nn



 

Vậy, 13113
lim lim
221 24
n
Snn





.
5
Giải phương trình: 2
43 12 125xxxxxx  
Điều kiện:
40 5
30 3(*)
2
250
x
xx
x



Đặt

43 0tx xt
22
7212txx
Phương trình đã cho trở thành
22
7125 225225(1)
2
t
txxttxx

Xét hàm số

22
f
uu u với 0u
Ta có:

220, 0fu u u

Hàm số đồng biến trên

0; 
Khi đó:
125tx
hay 43 25xxx
2
2
7212 2 5
12 1
x
xx
xx x


22
1189
4
12 2 1
xx
xx x x


(thỏa mãn (*) )
Vậy nghiệm của phương trình là: 189
4
x
.
6
Một hộp có 50 quả cầu được đánh số từ 1 đến 50. Lẫy ngẫu nhiên 3 quả cầu từ hộp đó.
Tính xác suất để tích 3 số ghi trên 3 quả cầu lấy được là một số chia hết cho 8.
Có 3
50
C cách lấy ra 3 quả cầu từ 50 quả cầu đã cho
Chia 50 quả cầu trong hộp thành 4 nhóm:
Nhóm 1: gồm 25 quả cầu mang số lẻ
Nhóm 2: gồm 13 quả cầu mang số chia hết cho 2 mà không chia hết cho 4
Nhóm 3: gồm 6 quả cầu mang số chia hết cho 4 mà không chia hết cho 8
Nhóm 4:
g
ồm 6 q
u
ả c
ầ
u
man
g
số chia hế
t
cho 8.
Để tích 3 số ghi trên 3 quả cầu lấy được là một số không chia hết cho 8 thì có 4 trường hợp
sau xảy ra:
TH1) 1 quả thuộc nhóm 1 và 2 quả thuộc nhóm 2: có 12
25 13
C.C cách lấy
TH2) 2 quả thuộc nhóm 1 và 1 quả thuộc nhóm 2: có 21
25 13
C.C cách lấy
TH3) 2 quả thuộc nhóm 1 và 1 quả thuộc nhóm 3: có 21
25 6
C.C
cách lấy
TH4) 3 quả thuộc nhóm 1: có 3
25
C cách lấy
Vậy xác suất cần tính là: P
12 21 21 3
25 13 25 13 25 6 25
3
50
C.C C.C C.C C 193
1
392
C
+++
=- =
7
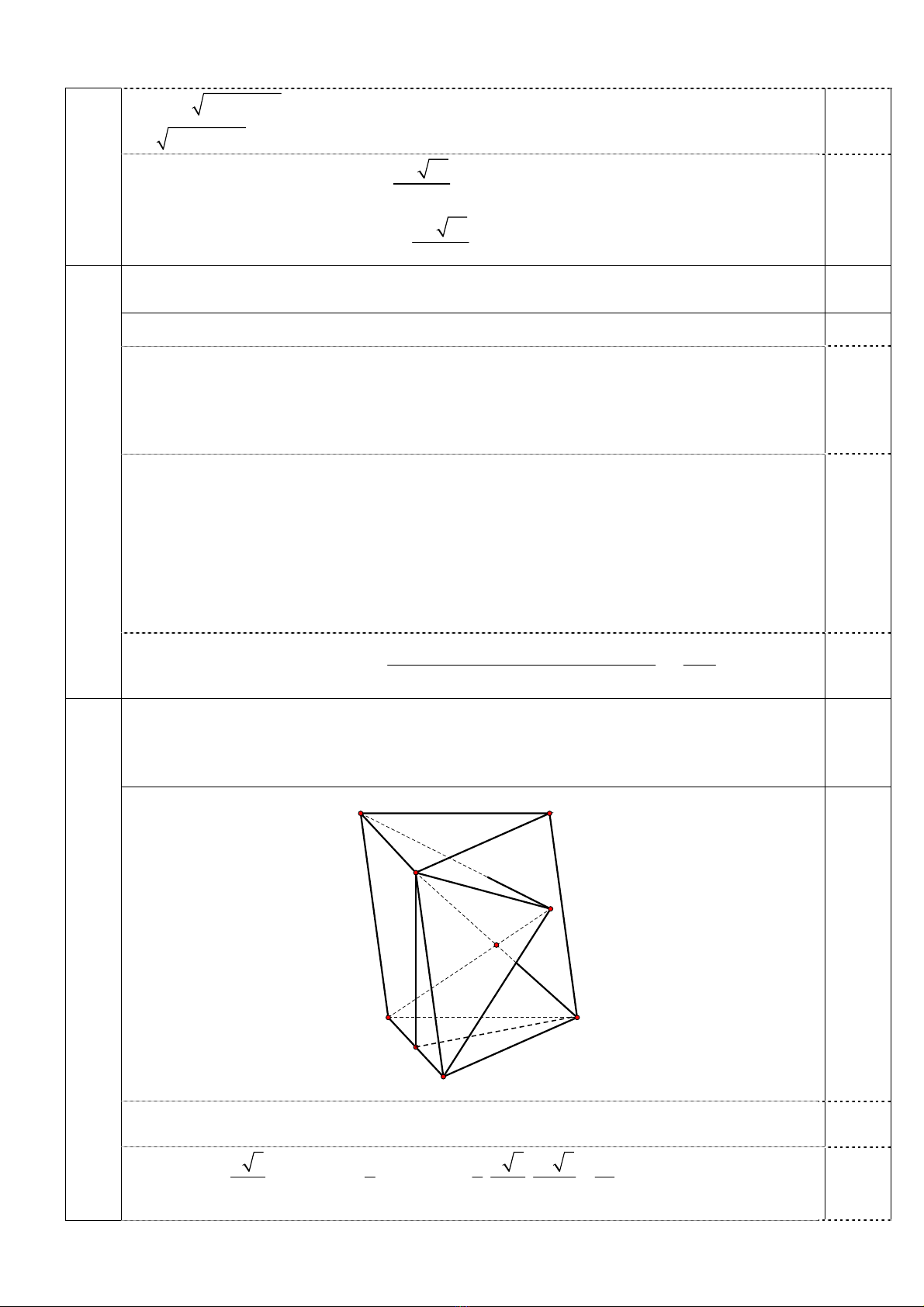
Cho hình lăng trụ .
A
BC A B C

có đáy là tam giác đều cạnh ,aAA a
. Hình chiếu vuông
góc của
A
trên mặt phẳng

A
BC trùng với trung điểm cạnh .
A
B Gọi
I
là trung điểm
của ,
A
C
điểm S thỏa mãn 2.
I
BSI
 
Tính theo a thể tích khối chóp ..SAABB

Gọi
H
là trung điểm của

A
B A H ABC CH AA B B


Ta có:
23
.
31133
...
233224
CAABB AABA
aaaa
CH V CH S
 

S
I
H
B
'C'
C
B
A
A
'