PHÒNG GD&ĐT VĨNH LỘC
CỤM TRUNG HỌC CƠ SỞ
ĐỀ GIAO LƯU HỌC SINH GIỎI LỚP 6,7,8
NĂM HỌC 2022 - 2023
Môn thi: Toán 6
Thời gian: 150 phút (không kể thời gian giao đề)
Ngày giao lưu: 22/ 3 / 2023
(Đề thi gồm có 01 trang, có 05 câu)
Câu 1: (4.0 điểm) Thực hiện phép tính:
1. A= 2
7∙9
14 +2
7∙5
14
2.
( ) ( ) ( )
20...321
20
1
...321
3
1
21
2
1
1+++++++++++=
B
3.
( )
34813
4
946
)27.(8.23.2.4
8.39.4.5
−+
−−
=C
4. D =
11 1 1
...
4.9 9.14 14.19 64.69
+ + ++
Câu 2: (4.0 điểm) Tìm x, biết:
1.
x (x 1) (x 2) ... (x 99) 14950+++++++ =
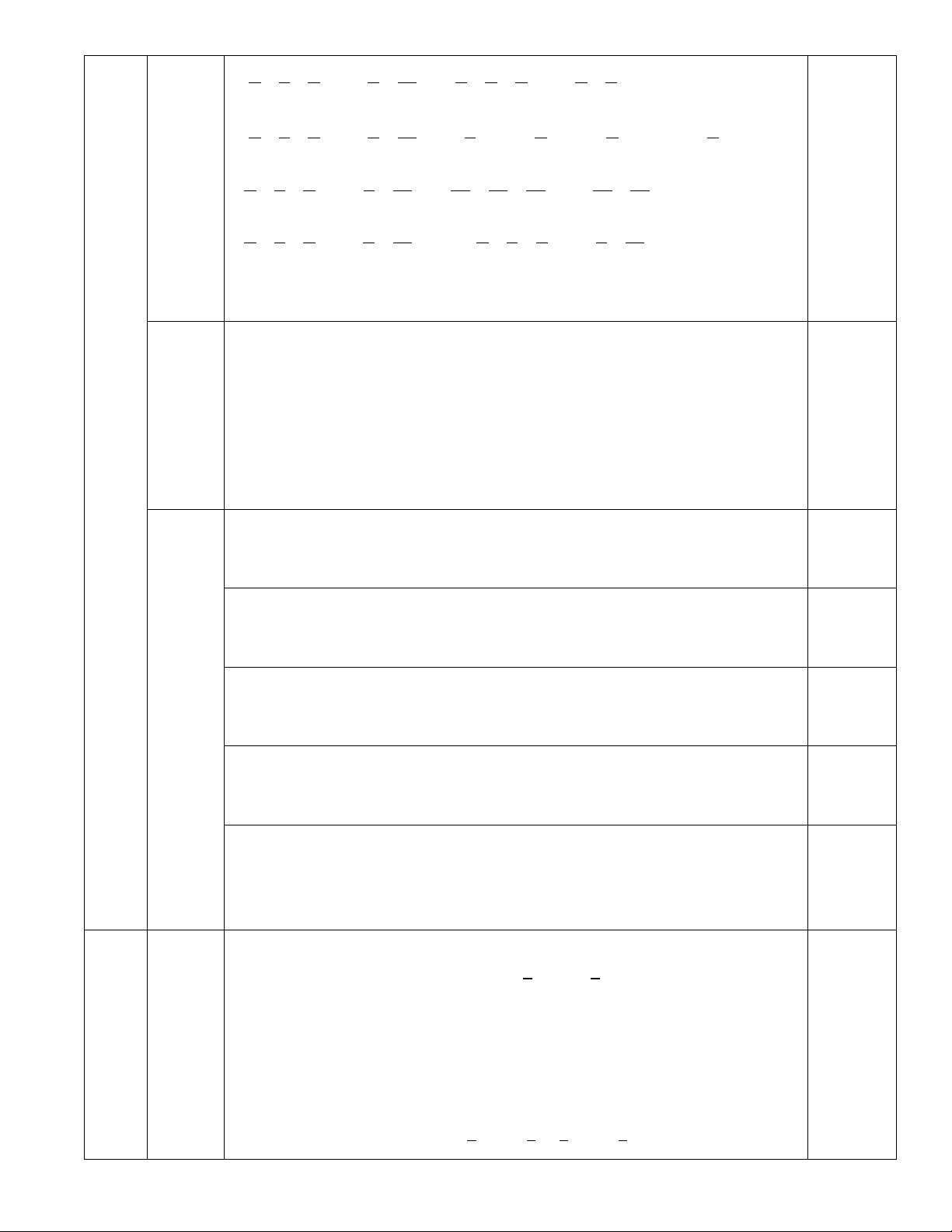
2.
1
9
2
8
...
7
3
8
2
9
1
10
1
9
1
...
4
1
3
1
2
1+++++=
+++++ x
3.
( )
2
4 3 51 :3 2 14x− ⋅+ − =


4.
Câu 3: (4.0 điểm)
1. Tìm số tự nhiên n sao cho 2n+3n=5n
2. Tìm số nguyên x, y biết x2y – x + xy = 6
Câu 4: (6.0 điểm)
1. Trên tia Ox lấy hai điểm M và N, sao cho OM = 3cm và ON = 7cm.
a. Tính độ dài đoạn thẳng MN.
b. Lấy điểm P trên tia Ox, sao cho MP = 2cm. Tính độ dài đoạn thẳng OP.
2. Cho 30 điểm trong đó có đúng 5 điểm thẳng hàng (ngoài ra không còn 3 điểm
nào thẳng hàng). Qua 2 điểm ta vẽ một đường thẳng. Hỏi có tất cả bao nhiêu đường
thẳng.
3. Tính diện tích hình chữ nhật ABCD, biết BE = CE = CF = 1
3 CD, diện tích
tam giác AEF bằng 50cm2. A B
E
D F C
Câu 5: (2.0 điểm) Cho n là số nguyên dương và m là ước nguyên dương của
2
2n
.
Chứng minh rằng :
2
nm+
không là số chính phương.
.......................................................Hết.........................................................................
Họ tên học sinh :........................................................... ; Số báo danh..........................
Cán bộ coi giao lưu học sinh giỏi không giải thích gì thêm.
Đề chính thức
PHÒNG GD&ĐT VĨNH LỘC
CỤM TRUNG HỌC CƠ SỞ
HƯỚNG DẪN CHẤM ĐỀ GIAO LƯU HỌC SINH GIỎI
LỚP 6,7,8
NĂM HỌC 2022 - 2023
Môn thi: Toán 6
Thời gian: 150 phút (không kể thời gian giao đề)
Ngày giao lưu: 22/ 3 / 2023
Câu
Ý
Nội dung
Điểm
Câu
1
(4.0đ)
1
(1.0 đ)
A =
2
7∙
9
14 +
2
7∙
5
14
= 2
7�9
14 +5
14�
=2
7∙1
= 2
7
0,5
0,25
0,25
2
(1.0đ)
( ) ( ) ( )
( ) ( )
11 1
1 1 2 1 2 3 1 2 3 ... 20
2 3 20
1 2.3 1 3.4 1 20.21
12 2 3 2 20 2
234 21
222 2
1 1 1 20.21
2 3 4 21 1 2 3 4 20 10 115
2 2 22
B
B
B
B
= + + + + + +⋅⋅⋅+ + + + +
= + ⋅ + ⋅ +⋅⋅⋅+ ⋅
= + + +⋅⋅⋅+
= + + +⋅⋅⋅+ = + + + +⋅⋅⋅+ = ⋅ + =
0,25
0,25
0,5
3
(1.0đ)
𝐶𝐶=
5. 46. 94−39.(−8)4
4. 213. 38+ 2. 84. (−27)3
= 5. 46. 94−39. 84
4. 213. 38−2. 84. 273
= 5. 212. 38−39. 212
215. 38−213. 39=212. 38(5−3)
213. 38(22−3)=212. 38. 2
213. 38= 1
0,25
0,75
4
(1.0đ)
D =
11 1 1
...
4.9 9.14 14.19 64.69
+ + ++
=
1111 1 1 1 1 1
( ... )
5 4 9 9 14 14 19 64 69
−+−+−++−
=
11 1
()
5 4 69
−
=
13
276
0,5
0,5
Câu
2
(4.0đ)
1
(1.0đ)
x (x 1) (x 2) ... (x 99) 14950+++++++ =
100x (1 2 3 ... 99) 14950
100x 4950 14950
100x 10000
x 100
+ +++ + =
+=
=
=
0,25
0,25
0,25
0,25
2
(1.0đ)
11
2
8
...1
7
3
1
8
2
1
9
1
10
1
9
1
...
4
1
3
1
2
1
1
9
2
8
...
7
3
8
2
9
1
10
1
9
1
...
4
1
3
1
2
1
+
+++
++
++
+=
+++++
+++++=
+++++
x
x
10
10
2
10
...
7
10
8
10
9
10
10
1
9
1
...
4
1
3
1
2
1+++++=
+++++ x
10
10
1
9
1
...
4
1
3
1
2
1
10
10
1
9
1
...
4
1
3
1
2
1=⇒
+++++=
+++++ xx
Vậy x=10
0,25
0,25
0,5
3
(1.0đ)
( )
4 3 51 :3 18x− ⋅+ =


( )
4 3 51 54x− ⋅+ =
(4 – x ).3 = 3
4 – x = 1
3x=
0,25
0,25
0,25
0,25
4
(1.0đ)
14. 72021 = 35. 72021 −3.49𝑥𝑥
3.49𝑥𝑥= 35. 72021 −14. 72021
3. 72𝑥𝑥 = 5.7. 72021 −2.7. 72021
0,25
3. 72𝑥𝑥 = 5. 72022 −2. 72022
3. 72𝑥𝑥 = 5. 72022 −2. 72022
0,25
3. 72𝑥𝑥 = 72022(5−2)= 3. 72022
72𝑥𝑥 = 72022
0,25
2𝑥𝑥= 2022
𝑥𝑥= 2022 : 2 = 1011
Vậy x=1011
0,25
Câu
3
(4.0đ)
1
(2.0đ)
Chia hai vÕ cho 5n, ta ®îc:
�2
5�𝑛𝑛+�3
5�𝑛𝑛= 1 (1)
+Víi n = 0
⇒
vÕ tr¸i cña (1) b»ng 2 (lo¹i)
+ Víi n = 1 th× vÕ tr¸i cña (1) b»ng 1 ( ®óng)
+ Víi n
2≥
th×:
�2
5
�𝑛𝑛<2
5
;�3
5
�𝑛𝑛<3
5
0,5
0,25
0,25
0,5
Nªn: �2
5�
𝑛𝑛
+�3
5�
𝑛𝑛
<2
5+1
5= 1 ( lo¹i)
VËy n = 1
0,25
0,25
2
(2.0đ)
x2y – x + xy = 6
⇒(𝑥𝑥2𝑦𝑦 − 𝑥𝑥)+𝑥𝑥𝑦𝑦 − 1 = 5
⇒ 𝑥𝑥(𝑥𝑥𝑦𝑦 − 1)+𝑥𝑥𝑦𝑦 − 1 = 5
⇒(𝑥𝑥𝑦𝑦 − 1)(𝑥𝑥+ 1) = 5
Mà 5 = 1.5 = (-1)(-5)
Ta có bảng sau:
x + 1
-5
-1
1
5
xy - 1
-1
-5
5
1
x
-6
-2
0
4
y
0
2
Vô lý
1
2( Loại)
Vậy có 2 cặp (x,y) thõa mãn là: (-6;0); (-2;2).
0,25
0,25
0,25
0,25
0,75
0,25
Câu
4
(6.0đ)
1.a
(1.0đ)
Do M, N cùng thuộc tia Ox mà OM < ON nên M nằm giữa hai
điểm O và N
OM MN ON⇒+=
3 7 7 3 4( )MN MN cm⇒+ =⇒ =−=
Vậy MN = 4(cm)
0,5
0,5
1.b
(1.0đ)
TH1: Nếu P nằm giữa M và N thì M nằm giữa O và P
⇒
OP = OM + MP
⇒
OP = 3 + 2 = 5(cm).
TH2: Nếu Nếu P nằm giữa O và M
⇒
OM = OP + PM
⇒
3 = OP + 2
⇒
OP = 1(cm).
0.5
0,5
2
(2.0đ)
Giả sử có 30 điểm trong đó không có ba điểm nào thẳng hàng thì
số đường thẳng là: 30(30-1):2=435 (đường thẳng)
Với 5 điểm, trong đó không có 3 điểm nào thẳng hàng thì vẽ
được:
5(5-1):2=10 (đường thẳng)
Nếu 5 điểm này thẳng hàng thì chỉ vẽ được 1 (đường thẳng)
0.5
0,5
0,5
P
P
N
M
x
O
Do đó số đường thẳng giảm đi là: 10-1=9 (đường thẳng)
Vậy vẽ được 435-9=426 (đường thẳng)
0,25
0,25
3
(2.0đ)
Đặt BE = CE = CF = x .
Ta có: BC = 2x ; DC = 3x.
Khi đó: SABCD = SADF + SABE + SCEF + SAEF
Hay 2x.3x = 1
2.2x.2x + 1
2.x.3x + 1
2.x.x + 50
Suy ra: 2x2 = 50
x2 = 25
x = 5
Vậy SABCD = 2.5.3.5 = 150cm2
0.5
0,5
0,5
0,5
Câu
5
(2.0đ)
Giả sử:
2
nm+
là số chính phương
Đặt:
( )
22
n mkkN+= ∈
(1)
Theo bài ra ta có:
( )
2
22
2n
n mp p N m p
= ∈ =>=
Thay vào (1) ta được :
( )
( )
22
2 222 22222
222
n
n k n p pn p k n p p pk
p
+==> + = => +=
Do
( )
2
2
,n pk
là các số chính phương
nên
2
2pp+
là số chính phương.
Mặt khác:
( )
2
22 2
21 2pppp pp<+<+=>+
không là số chính
phương (Mâu thuẫn với giả sử)
Vậy
2
nm+
không là số chính phương.
0.5
0,5
0,5
0,5
Chú ý:
1) Nếu thí sinh làm bài không theo cách nêu trong đáp án nhưng đúng thì cho đủ số
điểm từng phần như hướng dẫn quy định.
2) Bài hình (Câu 4) không vẽ hình hoặc vẽ hình sai cơ bản thì không chấm điểm.