KH I 11_ Đ 1Ố Ề
Câu I ( 4 đi m ):ể
1. Cho hàm s ố
2 3 2
2( 1) ( 1) (1),y x m x m m= − − − + +
v i m là tham s . Tìm ớ ố
m
đ đ th hàm s (1) ể ồ ị ố
c t tr c hoành t i 2 đi m có hoành đ ắ ụ ạ ể ộ
1 2
,x x
th a mãn ỏ
1 2 4x x+
. V i các giá tr ớ ị m đó hãy tìm giá tr ị
l n nh t và giá tr nh nh t c a bi u th c sau: ớ ấ ị ỏ ấ ủ ể ứ
3 3
1 2 1 2 1 2
(3 3 8)P x x x x x x= + + + +
2. Tìm h s c a ệ ố ủ
2017
x
trong khai tri n c a ể ủ
2 1
(2 )n
x x −
−
bi t ế
2 2 2 2
2 3 4
1 1 1 1 2016
... 2017
n
A A A A
+ + + + =
.
Câu II ( 4 đi m ): ểCho ph ng trình: ươ
1. Gi i ph ng trình khi ả ươ
3m=
.
2. Tìm m đ ph ng trình đã cho có 10 nghi m thu c ể ươ ệ ộ
(0;3 )
π
.
Câu III ( 2 đi m ):ể Cho
, ,abc
là ba s th c d ng th a mãn đi u ki n ố ự ươ ỏ ề ệ
3.ab bc ca
+ + =
Ch ng minh r ng: ứ ằ
2 2 2
1 1 1 1 .
1 ( ) 1 ( ) 1 ( )a b c b c a c a b abc
+ +
+ + + + + +
Câu IV ( 4 đi m ):ể
1. Gi i h ph ng trình: ả ệ ươ
32222
222
176121
4314
yxxyx
xyxyyx
2. M t h p đng 50 viên bi đc đánh s t 1 đn 50, ch n ng u nhiên 3 viên bi. Tính xác su t ộ ộ ự ượ ố ừ ế ọ ẫ ấ đ ể
t ng các s ghi trên 3 viên bi ch n đc là m t s chia h t cho 3.ổ ố ọ ượ ộ ố ế
Câu V ( 2 đi m ):ể Trong m t ph ng ặ ẳ v i h ớ ệ t a đ ọ ộ Oxy, cho tam giác ABC vuông t i ạA. Đi m ểD là
chân đng phân giác trong góc ườ A, các đi m ểM, N l n l t là hình chi u vuông góc c a ầ ượ ế ủ D lên AB và
AC. Đng tròn ườ
( )C
có ph ng trình: ươ
2 2 4 2 4 0x y x y+ + − − =
ngo i ti p tam giác ạ ế DMN . G i ọH là
giao đi m ểBN và CM, đng th ng ườ ẳ AH có ph ng trình ươ
0103: yx
. Tìm t a đ các đi m ọ ộ ể A, B và
C bi t hoành đ c a đi m ế ộ ủ ể A là s nguyên.ố
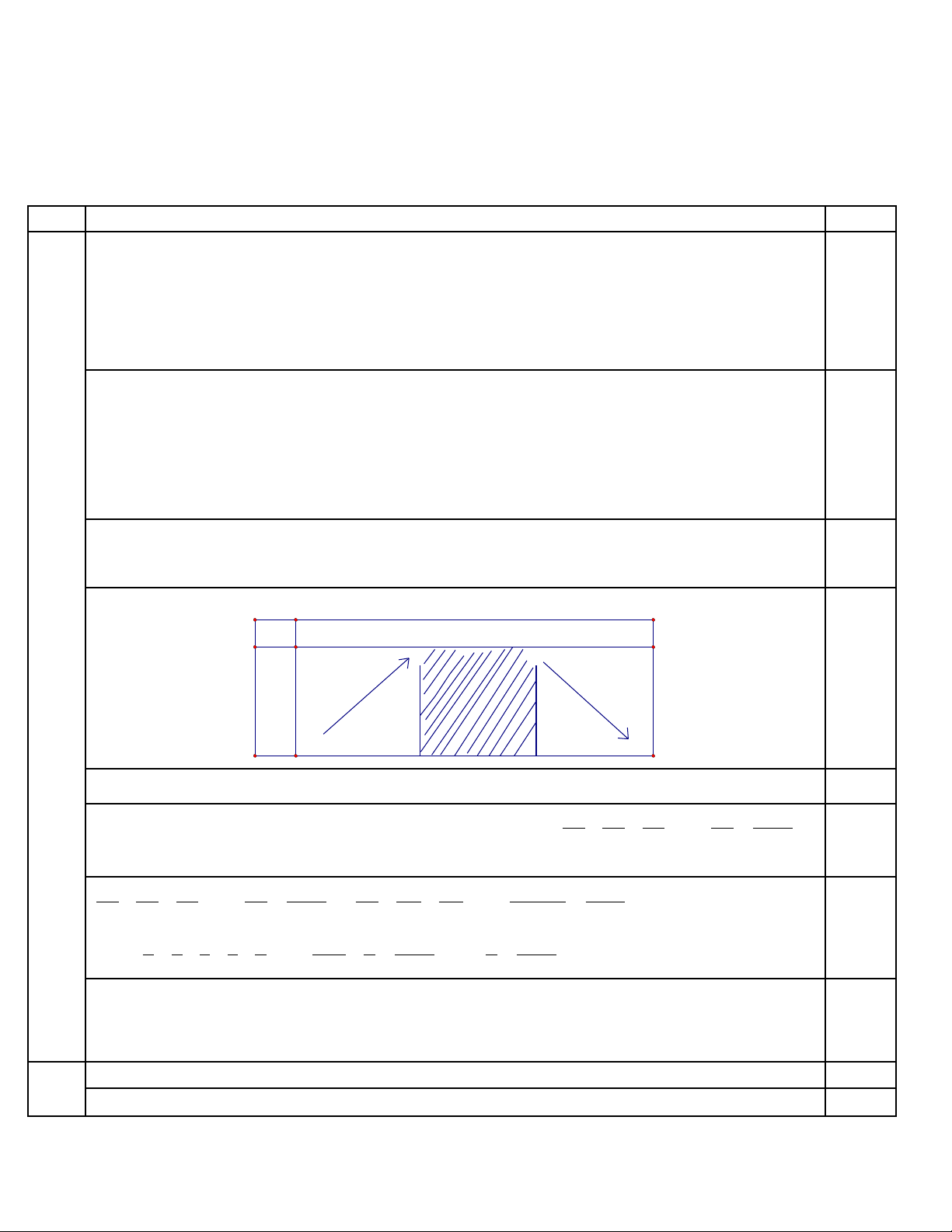
Câu VI ( 4 đi m ):ể Cho t di n đu ứ ệ ề ABCD c nh ạa. M và P là hai đi m di đng trên các c nh ể ộ ạ AD và BC
sao cho
(0 ).AM CP x x a= = < <
M t m t ph ng ộ ặ ẳ
( )
α
đi qua MP và song song v i ớCD c t t di nắ ứ ệ
ABCD theo m t thi t di n.ộ ế ệ
1. Thi t di n trên là hình gì?ế ệ
2. Tính x đ thi t di n có di n tích nh nh t.ể ế ệ ệ ỏ ấ
H và tên thí sinh: ………………………………………………. S báo danh: ……………………….ọ ố
Giám th 1: ……………………………………… Giám th 2: …………………………………..………ị ị
--------------------------- H t ------------------------------ế
Đ thi g m 6 câu trong 1 trangề ồ
Môn TOÁN – Kh i 11 – Đ 1ố Ề
CÂU N I DUNGỘĐI MỂ
Câu
I
1) Cho hàm s ố
( ) ( )
2
2 3
2 1 1y x m x m m= − − − + +
(1), v i m là tham s . Tìm ớ ố
m
đ đ th ể ồ ị
hàm s (1) c t tr c hoành t i 2 đi m có hoành đ ố ắ ụ ạ ể ộ
1 2
,x x
th a mãn:ỏ
1 2
4x x
+
. V i các ớ
giá tr m đó hãy tìm giá tr l n nh t và giá tr nh nh t c a bi u th c sau:ị ị ớ ấ ị ỏ ấ ủ ể ứ
( )
3 3
1 2 1 2 1 2
3 3 8P x x x x x x
= + + + +
2,0
Ph ng trình hoành đ giao đi m: ươ ộ ể
( ) ( )
2
2 3
2 1 1 0x m x m m− − − + + =
có hai nghi m ệ
1 2
,x x
th aỏ
mãn
1 2
4x x
+
( )
( )
2
1 2
2
4 0
' 0 2 0
2 0
42 3
2 1 4 3
m
m m m
m
x x m
mm
>
− >
∆ > − < <
� �
� � � �
− < <
� � �
+ <
−
� �
0,5
Theo đnh lí Viet ta có ị
( ) ( )
2
3
1 2 1 2
2 1 , 1x x m x x m m
+ = − = − + +
suy ra
( ) ( ) ( )
3 3 2
3 2
1 2 1 2
8 8 1 8 8 1 16 40P x x x x m m m m m
= + + = − − + + = − +
0,5
B ng bi n thiênả ế
-24
16
-144
0
3
2
0
-2
P
m
0,5
T b ng bi n thiên suy ra hàm s có GTNN là -144 khi m = - 2 và GTLN là 16 khi m = 2.ừ ả ế ố 0,5
Tìm h s c a xệ ố ủ 2017 trong khai tri n c a ể ủ
( )
1
2
2
n
x x
−
−
bi t ế
2 2 2 2
2 3 4
1 1 1 1 2016
... 2017
n
A A A A
+ + + + =
.
2,0
2 2 2 2
2 3 4
1 1 1 1 2016 1 1 1 1 2016
... ...
2017 1.2 2.3 3.4 ( 1) 2017
n
A A A A n n
+ + + + = + + + + =�−
1 1 1 1 1 1 1 2016 1 2016
1 ... 1 2017
2 2 3 3 4 1 2017 2017 n
n n n
− + − + − + + − = − = =� � �
−
1.0
( ) ( )
2016 2016
1 2016
2 2 2 2016 2016 2016
2016 2016
0 0
2 2 (2 ) ( ) 2 ( 1)
nk k k k k k k
k k
x x x x C x x C x
−− − +
= =
− = − = − = −
� �
=> x2017 ng v i k = 1 => H s c a xứ ớ ệ ố ủ 2017 là
1 1 2015
2016
2 ( 1) 4032C− = −
1.0
Cho ph ng trình: (3-m)sinx – 4sinươ 3x = (2-m)(1-cos2x) (1) 4,0
Gi i ph ng trình v i m = 3ả ươ ớ 2,0
Câu
II
V i m = 3 ta có: (1) ớ
– 4sin3x = cos2x – 1
3 2
4sin 2sin 0x x− =�
sinx=0
1
sinx= 2
0,5
0,5
0,5
2 ( )
6
52
6
x k
x k k Z
x k
= Π
Π
= + Π� �
Π
= + Π
0,5
Tìm m đ ph ng trình đã cho có 10 nghi m thu c ể ươ ệ ộ
( )
0;3
π
2,0
2
(1) s inx 4sin 2(2 ) s inx+m-3 0x m
� �
+ − =�� �
sinx 0 (2)
1
sinx (3)
2
3
sinx (4)
2
m
=
=�−
=
0,5
0,5
V×
( )
x 0;3
π
nªn pt(2) cã nghiÖm lµ
, 2x x
π π
= =
pt(3) nghiÖm lµ
5 13 17
, , ,
6 6 6 6
x x x x
π π π π
= = = =
VËy ®Ó pt (1) cã 10 nghiÖm thuéc
( )
0;3
π
th× pt(4) cã 4 nghiÖm pb kh¸c c¸c nghiÖm
cña pt(2) và pt(3).
BiÖn luËn ®Ó (4) cã 4 nghiÖm tho¶ m·n
lµ
−
� �
− < <
< <
3 1
4
2 2
3 3 5
0 1
2
m
m
m m
0,5
0,5
Cho
, ,abc
là ba s th c d ng th a mãn đi u ki n ố ự ươ ỏ ề ệ
3.ab bc ca
+ + =
Ch ng minh r ng: ứ ằ
2 2 2
1 1 1 1 .
1 ( ) 1 ( ) 1 ( )a b c b c a c a b abc
+ +
+ + + + + +
2,0
Áp d ng BĐT Cauchy cho 3 s d ng ta có: ụ ố ươ
2
3
3 3 ( ) 1ab bc ca abc abc
+ + =�
0,5
Suy ra:
2 2
2
1 1
1 ( ) ( ) ( ) 3 (1).
1 ( ) 3
a b c abc a b c a ab bc ca a a b c a
= + + = + + + +�+ +
0,5
Câu
III T ng t ta có: ươ ự
2 2
1 1 1 1
(2), (3).
1 ( ) 3 1 ( ) 3b c a b c a b c
+ + + +
C ng (1), (2) và (3) theo v v i v ta có:ộ ế ớ ế
2 2 2
1 1 1 1 1 1 1 1
( )
1 ( ) 1 ( ) 1 ( ) 3 3
ab bc ca
a b c b c a c a b c b c abc abc
+ +
+ + + + = =
+ + + + + + W
0,5
D u “=” x y ra khi và ch khi ấ ả ỉ
1, 3 1, ( , , 0).abc ab bc ca a b c a b c
= + + = = = = >�
0,5
Câu
IV
Gi i h ph ng trình: ả ệ ươ
32222
222
176121
4314
yxxyx
xyxyyx
2,0
Đi u ki n: ề ệ
3
x
. Gi i pt(1): ả
( )
( )
( )
2 2 2
4 1 3 4x y y x y x
+ + + + = + +
Ta có các BĐT:
( )
2
2
3
32
y x
y x + +
+
và
( )
( )
2
2
4 1
4 1 2
x y
x y + + +
+ +
4314 222
xyxyyx
. Đng th c x y ra ẳ ứ ả
3
2
xy
.
V y: ậ
2
(1) 3pt y x= +�
1,0
Thay
3
2
xy
vào (2) ta đc ph ng trìnhượ ươ
( )
3 2 2 3 2 23 3
2 2 1 6 1 2 3 1 6 1 0x x x x x x x x x x x
� �
+ − + = + + + − + + − + + =�� �
0,5
( )
( ) ( )
( )
3 2
2
22 23 3
1
2 3 1 0
1 1 6 1 6 1
x x x
x x x x x x
� �
� �
+ − + =�� �
+ + + + + + + +
� �
� �
( )
{ }
2
2 3 0 3;0;1x x x x
+ − = −� � �
V y h ph ng trình có nghi m là: ậ ệ ươ ệ
( )
( ) ( )
( ) ( ) ( )
{ }
; 0; 3 ; 0; 3 ; 1;2 ; 1; 2 ; 3;0x y
− − −�
0,5
M t h p đng 50 viên bi đc đánh s t 1 đn 50, ch n ng u nhiên 3 viên bi. Tính xácộ ộ ự ượ ố ừ ế ọ ẫ
su t ấ đ t ng các s ghi trên 3 viên bi ch n đc là m t s chia h t cho 3.ể ổ ố ọ ượ ộ ố ế
2,0
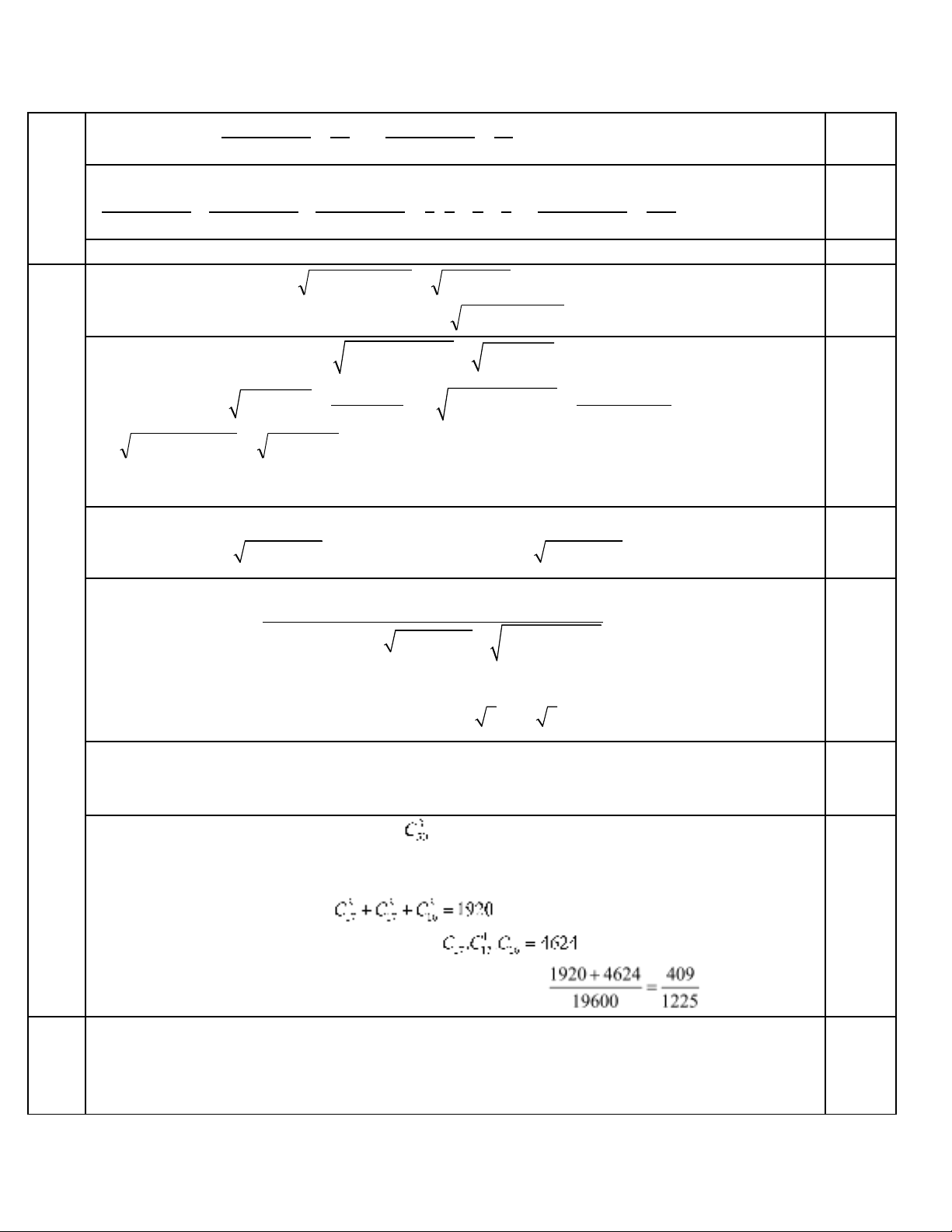
- S cách ch n 3 viên bi t 50 viên bi là ố ọ ừ
- Trong 50 viên bi ban đu đc chia làm ba lo i: có 17 viên bi ghi s chia cho 3 d 1; 17 viênầ ượ ạ ố ư
bi ghi s chia cho 3 d 2 và 16 viên bi ghi s chia h t cho 3.ố ư ố ế
TH1: Ch n 3 viên bi cùng lo i ọ ạ cách
TH2: 3 viên bi đc ch n m i viên m t lo i ượ ọ ỗ ộ ạ
V y xác su t đ ch n đc 3 viên bi th a mãn bài toán là: ậ ấ ể ọ ượ ỏ
0,5
0,5
0,5
0,5
Trong m t ph ng ặ ẳ v i h ớ ệ t a đ ọ ộ Oxy, cho tam giác ABC vuông t i ạA. Đi m ểD là chân
đng phân giác trong góc ườ A, các đi m ểM, N l n l t là hình chi u vuông góc c a ầ ượ ế ủ D
trên AB và AC. Đng tròn ườ
0424:)( 22 yxyxC
ngo i ti p tam giác ạ ế DMN .
2,0
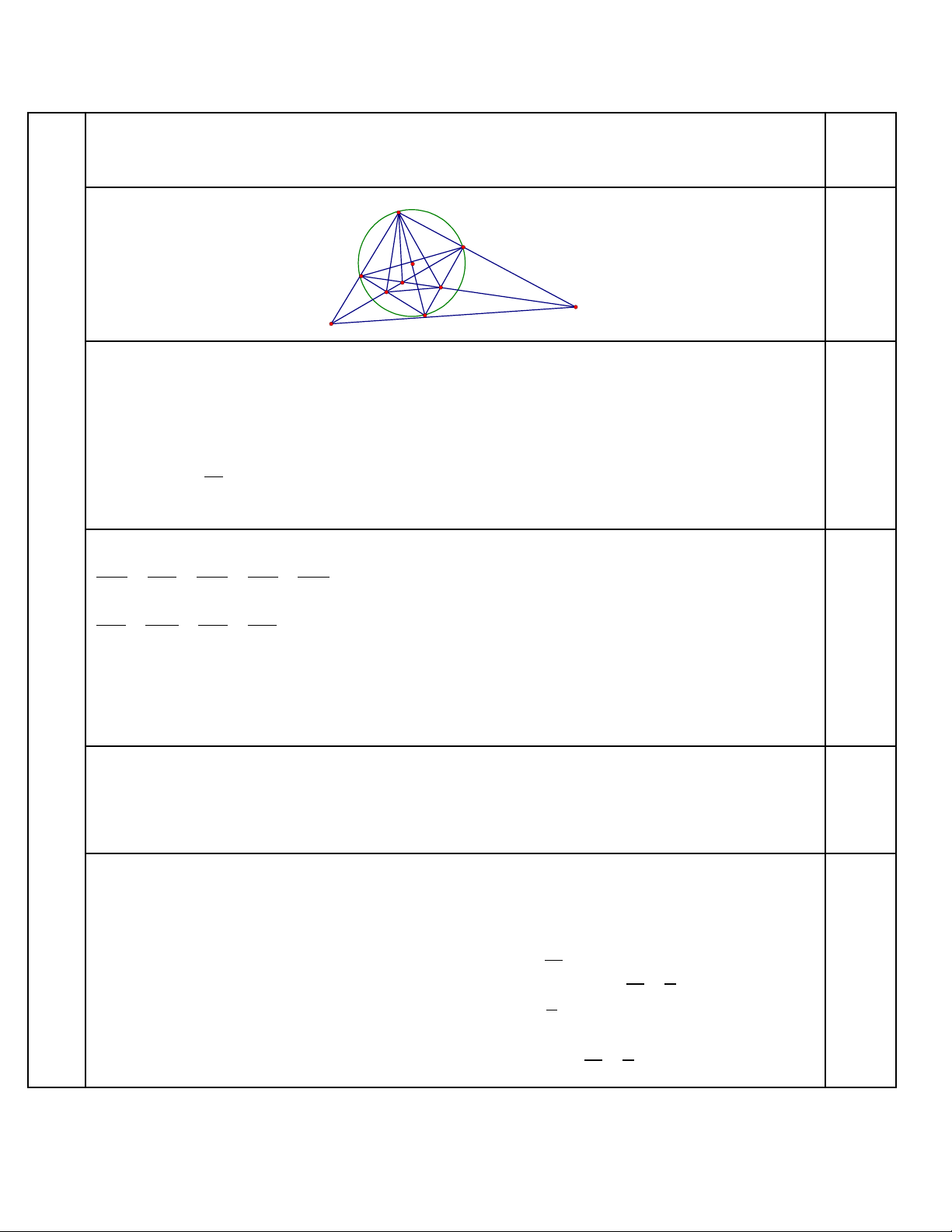
Câu
V
G i ọH là giao đi m ểBN và CM, đng th ng ườ ẳ AH có ph ng trình ươ
0103: yx
. Tìm
t a đ các đi m ọ ộ ể A, B và C bi t hoành đ c a đi m ế ộ ủ ể A là s nguyên.ố
D
K
E
F
H
I
A
C
B
M
N
Vì AMDN là hình vuông nên
)(CA
T a đ đi m A là nghi m c a h :ọ ộ ể ệ ủ ệ
)4;2(
4
;2
103
)(
5
19
;2
0103
0424
22
A
y
x
xy
Lxx
yx
yxyx
0,5
G i E,F là giao đi m BN v i DM,c a CM v i DN. Vì AMDN là hình vuông nênọ ể ớ ủ ớ
MD
ME
AN
ME
AC
MD
AC
AN
MC
MF
BCEFDCEF ////
AB
AN
AB
ND
AM
NF
AN
NF
ANF
và
BAN
đng d ng ồ ạ
AFBNNAFABN
T ng t ươ ự
AECN
H là tr c tâmự
AEF
BCAHEFAH
Đng tròn (C) có tâm ưở
)1;2(I
AMDN là hình vuông nên I là trung đi m c a AD. ể ủ
)2;2()1;2(),4;2( DIA
Đng th ng ườ ẳ
AHBC
nên BC có PT:
0830)2(32 yxyx
0,5
Ph ng trình AD là: ươ
2x
;
ADMN
t i I nên ph ng trình MN là: ạ ươ y = 1
T a đ đi m M và N là nghi m c a h :ọ ộ ể ệ ủ ệ
1
5;1
1
0424
22
y
xx
y
yxyx
)1;5()1;1( NvàM
ho c ặ
)1;1()1;5( NvàM
0,5
V i ớ
)1;5()1;1( NvàM
. AM có PT là:
02 yx
; AN có PT là:
06 yx
T a đ đi m B là nghi m c a h :ọ ộ ể ệ ủ ệ
)5;7(
5
7
02
083
B
y
x
yx
yx
T a đ đi m C là nghi m c a h :ọ ộ ể ệ ủ ệ
2
1
;
2
13
2
1
2
13
06
083 C
y
x
yx
yx
V i ớ
)1;5()1;1( NvàM
do vai trò c a B và C nh nhau nên ủ ư
2
1
;
2
13
B
;
5;7 C
0,5